Refer to our Texas Go Math Grade 7 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 7 Lesson 13.2 Answer Key Calculating and Comparing Simple and Compound Interest.
Texas Go Math Grade 7 Lesson 13.2 Answer Key Calculating Sales and Income Tax
Example 1.
Roberto’s parents open a savings account for him on his birthday. The account earns simple interest at an annual rate of 5%. They deposit $100 and will deposit $100 on each birthday after that. Roberto will make no withdrawals from the account for at least 10 years. Make a table to show how the interest accumulates over five years.
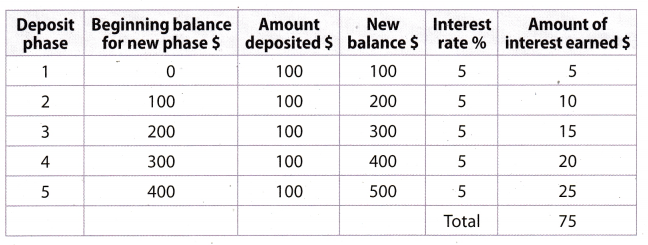
Roberto earns a total of $75 ¡n interest over the five years.
Reflect
Question 1.
Make a Prediction Predict how much simple interest Roberto will have earned after the tenth year. Suppose he continues to make no withdrawals. ______
Answer:
Amount of interest earned = New balance × interest rate
Write the interest rate as decimal. ie 5% = 0.05.
Every year we calculate simple interest on a new balance to find the amount of a interest earned.
Year 6
Amount of interest earned = $6000 × 0.05 = $30
Year 7
Amount of interest earned = $700 × 0.05 = $35
Year 8
Amount of interest earned = $800 × 0.05 = $40
Year 9
Amount of interest earned = $900 × 0.05 = $45
Year 10
Ainouiit of interest earned = $1,000 × 0.05 = $50
Roberto earns a total of $275 in interest after the tenth year.
Your Turn
Question 2.
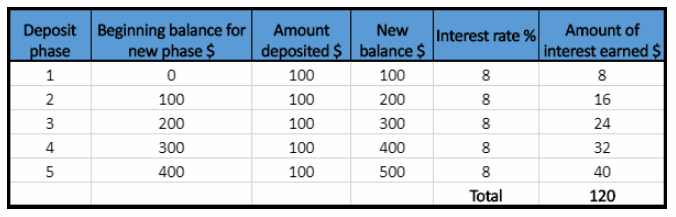
Each year Amy deposits $100 into an account that earns simple interest at an annual rate of 8%. How much interest will she earn over the first five years? How much will be in her account after that time?
Answer:
Amount of interest earned = New balance × interest rate
Write the interest rate as decimal. ie 8% = 0.08.
Every year we calculate simple interest on a new balance to find the amount of a interest earned.
Year 1
Amount of interest carnal = $100 × 0.08 = $8
Year 2
Amount of interest earned = $200 × 0.08 = $16
Year 3
Amount of interest earned = $300 × 0.08 = $24
Year 4
Amount of interest eariìed = $400 × 0.08 = $32
Year 5
Amount of interest earned = $500 × 0.08 = $40
Amy earns a total of $120 in interest after the fifth year.
Example 2.
On Claudia’s birthday, her parents open a savings account and deposit $100. They also deposit $100 each year after that on her birthday. The account earns interest at an annual rate of 5% compounded annually. Claudia will make no withdrawals from the account for at least 10 years. Make a table to find the ending balance in Claudia’s account after 5 years.
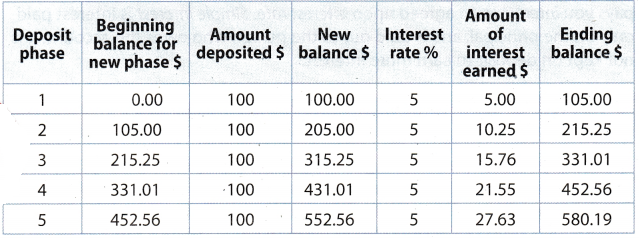
The total amount in the account at the end of the fifth year is $580.19.
Reflect
Question 3.
Does the balance of Claudia’s account change by the same amount each year? Explain why or why not.
Answer:
No, it does not, because it is the case of compound interest.
Compound interest is computed on the amount that includes the principal and any previously interest earned.
The beginning balance for new phase is actually the ending balance from the previous phase, which contains the interest earned in that previous phase.
Every year the interest is computed on that previous ending balance, which is different every year, and because of that the ending balance does not change by the same amount each year.
Question 4.
Would the total amount in the account after 5 years be greater if the interest rate were higher? Explain.
Answer:
Yes, it would.
If the interest rate were higher, the amount of interest earned in first year will be greater and the ending balance will be greater too.
It is compound interest and every next year the ending baLance wilL be greater, and because of that the total amount in the account after 5 years will be greater.
Your Turn
Question 5.
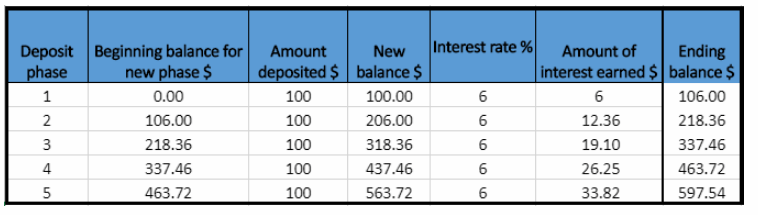
What If? Suppose the interest rate on Claudia’s account is 6% instead of 5%. How much will Claudia have in her account at the end of the fifth year? How does it compare to the amount in Example 2?
Answer:
New balance = Beginning balance for new phase + Amount deposited
Amount of interest earned = New balance × Interest rate
Ending balance = New balance + Amount of interest earned
Ending balance in the first year is the Beginning balance for new phase in the second year.
Hence, the Beginning balance for new phase is the Ending balance from the previous year.
Write the interest rate as decimal, ie 6% = 0.06.
Year 1
New balance in the first year is $100.
Amount of interest, earned = $100 × 0.06 = $6
Ending balance = $100 + $6 = $106
Year 2
New balance in the second year is the Ending balance from previous year plus Amount deposited, ie $106 + $100 = $206.
Amount of interest earned = $206 × 0.06 = $12.36
Ending balance = $206 + $12.36 = $218.36
Year 3
New balance in the third year is the Ending balance from previous year plus
Amount deposited, ie $218.36 + $100 = 8318.36.
Amount of interest earned = $318.36 × 0.06 = $19.10
Ending balance = $318.36 + $19.10 = $337.46
Year 4
New balance in the forth year is the Ending balance from previous year plus
Amount deposited. ie $337.46 + $100 = $437.46.
Amount of interest earned = $437.16 × 0.06 = $26.25
Ending balance = $437.46 + $26.25 = $463.72
Year 5
New balance in the fifth year is the Ending balance from previous year plus
Amount deposited. ie $463.72 + $100 = $563.72.
Amount of interest earned $563.72 × 0.06 = $33.82
Ënding balance = $563.72 + $33.82 = $597.54
The total amount on the Claudia’s account at the end of the fifth year is $597.54.
Compare the amount on Claudia’s account with interest rate of 6% and amount on account with interest rate of 5%(from Example 2) using subtraction:
$597.54 – $580.19 = $17.35
When the interest rate is higher, the amount on account is greater.
Example 3.
Jane has two savings accounts, Account S and Account C. Both accounts are opened with an initial deposit of $100 and an annual interest rate of 5%. No additional deposits are made, and no withdrawals are made. Account S earns simple interest, and Account C earns interest compounded annually. Which account will earn more interest after 10 years? How much more?
Answer:
Step 1
Find the total interest earned by Account S after 10 years.
Find the amount of interest earned in one year.
principal × Interest rate = Interest for 1 year
$100 × 0.05 = $5
Find the amount of interest earned in ten years.
Interest for 1 year × Number of years = Interest for 10 years
$5 × 10 = $50
Account S will earn $50 after 10 years.
Step 2
Find the final amount in Account C. Then subtract the principal to find the amount of interest earned.
A = P(1 + r)t
= 100 × (1 + 0.05)10
= 162.89
Account C will earn $162.89 – $100.00 = $62.89 after 10 years.
Step 3
Compare the amounts using subtraction: $62.89 – $50 = $12.89
Account C earns $12.89 more in compound interest after 10 years than Account S earns in simple interest.
Your Turn
Question 6.
What If? Suppose the accounts in Example 3 both have interest rates of 4.5%. Which account will earn more interest after 10 years? How much more?
Answer:
The account S earns simple interest, and account C earns interest compounded annually.
The principal for both accounts is $100.
Account S
Write interest rate as decimal. ie 1.5% = 0.045
Find the amount of interest earned in one year.
Principal × Interest rate = Interest in one year
$100 × 0.045 = $4.5
Now, find the amount of interest earned in ten tears.
Interest for 1 year × Number of years = Interest for 10 years
$4.5 × 10 = $45
Account S will earn $45 after 10 years.
Account C
Use the formula for compound interest compounded annually.
A= P(1 +r)t
where P is the principal, r is interest rate(in decimal), t is the time in years and A is the amount in the account after t years if no withdrawals are made.
Find the final amount in the account after 10 years.
Substitute 10 for t, 100 for P and 0.045 for r in the formula.
A = 100(1 + 0.045)10
A = 100(1.045)10
A = 100 . 1.55
A = 155
The final amount in account C is $155.
To find the amount of interest earned subtract principal from the final amount.
$155 – $100 = $55
Account C will earn $55 after 10 years.
Compare the amounts using subtraction:
$55 – $45 = $10
Account C will earn $10 more in compound interest after 10 years than account S earns in simple interest.
Texas Go Math Grade 7 Lesson 13.2 Guided Practice Answer Key
Question 1.
Each year on the same day, Hasan deposits $150 in a savings account that earns simple interest at an annual rate of 3%. He makes no other deposits or withdrawals. How much interest does his account earn after one year? After two years? After five years? (Example 1)
Answer:
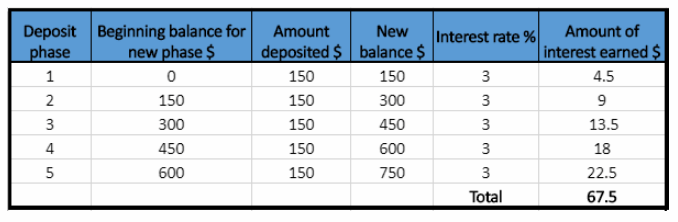
Amount of interest earned = New balance × Interest rate
Write the interest rate as decimal, ie 3% = 0.03.
Every year we calculate simple interest on a new balance to find the amount of a interest earned.
year 1
Amount of interest earned = $150 × 0.03 = $4.5
Year 2
Amount of interest earned = $300 × 0.03 = $9
Year 3
Amount of interest earned = $450 × 0.03 = $13.5
Year 4
Amount of interest earned = $600 × 0.03 = $18
Year 5
Amount of interest earned = $750 × 0.03 = $22.5
Hasan earns $4.5 in interest after the first year.
Hasan earns $4.5 + $9 = $13.5 in interest after the second year.
Hasan earns $67.5 in interest after the fifth year.
Keri deposits $100 in an account every year on the same day. She makes no other deposits or withdrawals. The account earns an annual rate of 4% compounded annually. Complete the table. (Example 2)
Question 2.
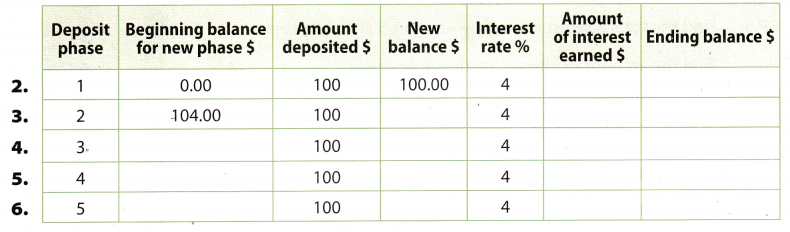
Answer:
Amount of interest earned = New balance × Interest rate
Ending balance = New balance + Amount of interest earned
Write the interest rate as decimal, ie % = 0.04.
Year 1
New balance in the first year is $100.
Amount of interest earned = $100 × 0.04 = $4
Ending balance = $100 + $4 = $104
Question 3.

Answer:
New balance = Beginning balance for new phase + Amount deposited
Amount of interest earned = New balance × Interest rate
Ending balance = New balance + Amount of interest earned
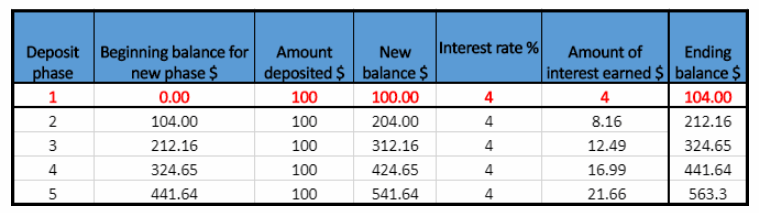
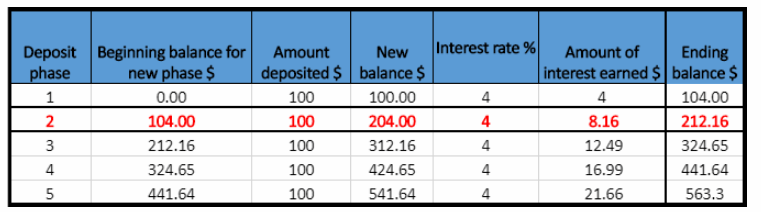
Year 2
New balance in the second year is the Ending balance front previous year plus Amount deposited. ie $104 + $100 = $201.
Amount of interest carried = $204 × 0.04 = $8.16
Ending balance = $204 + $8.16 = $212.16
Question 4.

Answer:
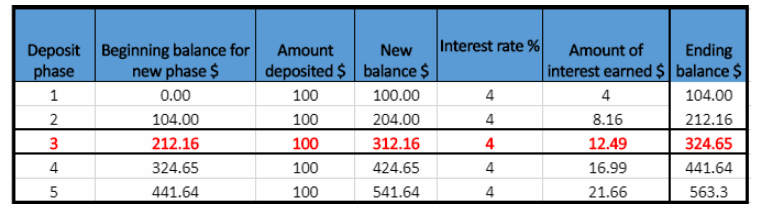
New balance = Beginning balance for new phase + Amount deposited
Amount of interest earned = New balance × Interest rate
Ending balance = New balance + Amount of interest earned
Year 3
New balance in the third year is the Ending balance from previous year plus Amount deposited, ie $212.16 + $100 = $312.16.
Amount of interest earned = $312.16 × 0.04 = $12.49
Ending balance = $312.16 + $12.49 = $324.65
Question 5.

Answer:
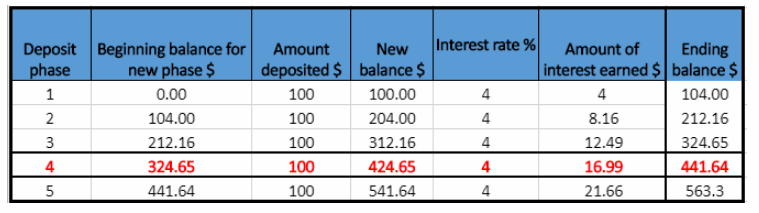
New balance = Beginning balance for new phase + Amount deposited
Amount of interest earned = New balance × Interest rate
Ending balance = New balance + Amount of interest earned
Year 4
New balance in the fourth year is the Ending balance from previous year plus Amount deposited. ie $324.65 + $100 = $424.65.
Amount of interest earned = $424.65 × 0.04 = $16.99
Ending balance = $424.65 + $16.99 = $441.64
Question 6.

Answer:
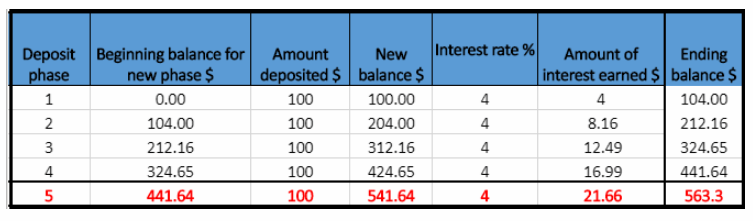
New baLance = Beginning baLance for new phase + Amount deposited
Amount of interest earned = New balance × Interest rate
Ending balance = New balance + Amount of interest earned
Year 5
New balance in the fifth year is the Ending balance from previous year plus Amount deposited. ie $441.64 + $100 = $541.64.
Amount of interest earned = $541.61 × 0.04 = $21.66
Ending balance $541.64 + $21.66 = $563.3
Question 7.
Theo deposits $2,000 deposit in a savings account earning compound interest at an annual rate of 5% compounded annually. He makes no additional deposits or withdrawals. Use the formula for compound interest to find the amount in the account after 10 years. (Example 3)
Answer:
Use the formula for compound interest compounded annually.
A = P(1 + r)t
where P is the principal, r is interest rate(in decimal), t is the time in years and A is the amount in the account after
t years if no withdrawals are made.
Find the final amount in the account after 10 years.
Substitute 10 for t, 2,000 for P and 0.05 for r in the formula.
A = 2,000(1 + 0.05)10
A = 2,000(1.05)10
A = 2,000 . 1.63
A= 3,260
The final amount in the account after 10 years is $3,260.
To find the amount of interest earned subtract principal from the final amount.
$3,260 – $2,000 = $1,260
Theo will earn $1,260 after 10 years.
Essential Question Check-In
Question 8.
Describe the difference between simple interest and compound interest.
Answer:
The simple interest is computed only on the principal, and the compound interest is computed on the amount that includes the principal and any previously interest earned.
Hence, amount of interest earned is greater when account earns a compounded annually, because the amount on
which interest is calculated is greater.
The simple interest is computed only on the principal, and the compound interest is computed on the amount that includes the principal and any previously interest earned.
Texas Go Math Grade 7 Lesson 13.2 Independent Practice Answer Key
Mia borrowed $5,000 from her grandparents to pay college expenses. She pays them $125 each month, and simple interest at an annual rate of 5% on the remaining balance of the loan at the end of each year.
Question 9.
How many months will it take her to pay the loan off? Explain.
Answer:
She pays $125 each month, and the loan to her grandparents is $5,000.
To find how many months will she take to pay the loan off, we have to divide the whole loan by the amount of monthly pay.
\(\frac{\$ 5,000}{\$ 125}\) = 40
She will pay off the loan for 40 months.
Question 10.
For how many years will she pay interest? Explain.
Answer:
Mia pays interest at the end of the year on the remaining balance of the loan.
As long as there is some amount of remaining balance of the loan at the end of the year, she will pay interest.
She pays monthly $125, which means that she pays yearly
$125 × 12 = $1,500
The remaining balance of the loan at the cud of the first year we get when we subtract the amount of the loan that has been paid that year from the whole loan.
First year she will pay $1,500 (plus the simple interest on the remaining balance of the loan, which we will not calculate in this Exercise).
The remaining balance at the end of the first year = $5,000 – $1,500 = $3,500
After the first year the loan is no longer $5,000 but $3,500.
To find the remiaining balance of the loan at the end of the second year we have to subtract the amount she pays yearly, ie $1,500 (the same amount every year), from the new amount of loan $3,500.
The remaining balance at the end of the second year $3,500 – $1,500 = $2,000
After the second year the loan is $2,000.
To find the remaining balance of the loan at the end of the third year we have to subtract the amount she pays yearly, ie $1,500, from the new amount of loan, ie $2,000.
The remaining balance at the end of the third year = $2,000 – $1,500 = $500
In the fourth year the remaining balance of the loan is 8500 which she will pay for the first four months of that year.
By the end of the fourth year she will not have any remaining balance of the loan to calculate the simple interest.
Hence, she will pay interest for three years.
Question 11.
How much simple interest will she pay her grandparents altogether? Explain.
Answer:
Min pays simple interest on the remaining balance of the loan each year, so we have to calculate the simple interest at the end of each year.
The simple interest = The remaining balance of the loan × Annual rate(in decimal)
She pays monthly $125, which means that she pays yearly
$125 × 12 = $1,500
Year 1
The remaining balance of the loan at the end of the first year we get when we subtract the amount of the loan that has been paid that year from the whole loan.
The remaining balance at the end of the first year = $5,000 – $1,500 = $3,500
After the first year the remaining balance of the loan is $3,500.
The simple interest = $3, 500 × 0.05 = $175
The simple interest at the end of the first year is $175.
Year 2
After the first year the loan is $3,500.
To find the remaining balance of the loan at the end of the second year we have to subtract the amount she pays yearly, which is the same amount every year, ie $1,500, from the new amount of loan, ie $3,500.
The remaining balance at the end of the second year = $3, 500 – $1,500 = $2,000
After the second year the remaining balance of the loan is $2,000.
The simple interest $2, 000 × 0.05 = $100
The simple interest at the end of the second year is $100.
Year 3
After the second year the loan is $2,000.
To find the remaining balance of the loan at the end of the third year we have to subtract the amount she pays yearly, ie $1,500, from the new amount of loan. ie $2,000.
The remaining balance at the end of the third year = $2,000 – $1,500 = $500
After the third year the remaining balance of the loan is $500.
The simple interest = $500 × 0.05 = $25
The simple interest at tile end of the second year is $25.
In the fourth year the remaining balance of the loan is $500 which she will pay for the first four months of that year.
Hence, by the end of the fourth year she will not have any remaining balance of the loan to calculate the simple interest.
Add all the simple interest we previously calculate to find the simple interest she will have to pay to her grandparents altogether.
The simple interest = $175 + $100 + $25 = $300
Altogether she will pay the simple interest of $300.
Question 12.
Roman saves $500 each year in an account earning interest at an annual rate of 4% compounded annually. How much interest will the account earn at the end of each of the first 3 years?
Answer:
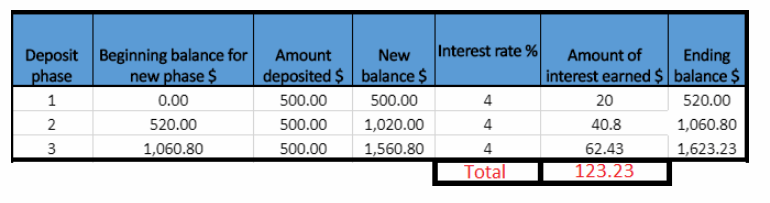
Each year Roman saves $500 which represents the amount deposited for each year.
Amount of interest earned = New balance × Interest rate
Ending balance = New balance + Amount of interest earned
Write the interest rate as decimal, ie 4% = 0.04.
Year 1
New balance in the first year is $500.
Amount of interest earned = 8500 × 0.04 = $20
The interest earned at the end of the first year is $20.
Ending balance = $500 + $20 = $250
Year 2
New balance in the second year is the Ending balance from previous year plus Amount deposited. ie $520 + $500 = $1,020.
Amount of interest earned = $1.020 × 0.04 = $40.8
The interest earned at the cud of the second year is $40.8.
Ending balance = $1,020 + $40.8 = $1,060.8
Year 3
New balance in the third year is the Ending balance from previous year plus Amount deposited, ie $1,060.8 + $500 = $1,560.8.
Amount of interest earned = $1.560.8 × 0.04 = $62.43
The interest earned at the end of the third year is $62.43.
Ending balance = $1,560.8 + $62.43 = $1,623
The interest earned at the end of the first year is $20.
The interest earned at the end of the second year is $40.8.
The interest earned at the end of the third year is $62.43.
Question 13.
Jackson started a savings account with $25. He plans to deposit $25 each month for the next 12 months, then continue those monthly deposits in following years. The account earns interest at an annual rate of 4% compounded annually, based on his final yearly balance. Fill in the chart to find out how much money he will have in the account after 3 years.
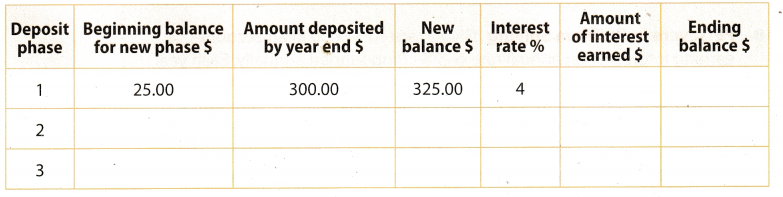
Answer:

Each month Jackson plans to deposit $25, and the year has 12 months. hence
Amount deposited by year end = Monthly deposit × 12
Amount deposited by year end = $25 × 12 = $300
Amount of interest earned = New balance × Interest rate
Ending balance = New balance + Amount of interest earned
Write the interest rate as decimal, ie % = 0.04.
Year 1
New balance in the first year is $325.
Amount of interest earned = $325 × 0.04 = $13
Ending balance = $325 + $13 = $338
Year 2
New balance in the second year is the Ending balance from previous year plus Amount deposited, ie $338 + $300 = $638.
Amount of interest earned = $638 × 0.04 = $25.52
Ending balance = $638 + 825.52 = $663.52
Year 3
New balance in the third year is the Ending balance from previous year plus Amount deposited. ie $663.52 + $300 = $963.52.
Amount of interest earned = $963.52 × 0.04 = $38.54
Ending balance = $963.52 + $38.54 = $1,002.06
After three years Jackson will have $1,002.06 on his account.
Question 14.
Communicate Mathematical Ideas Look back at Exercise 13. Suppose Jackson increased the initial deposit by $75, but made the same monthly deposits. Would the balance at the end of every year increase by $75?
Answer:
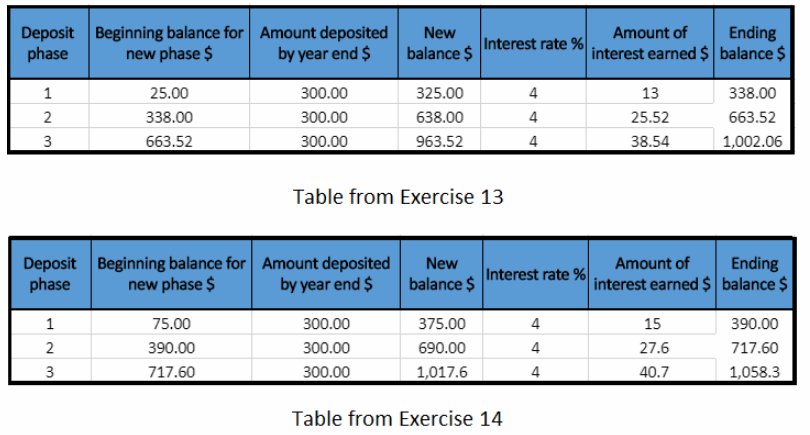
The Ending balance in the first year with beginning balance of $25 is $338.
The Ending balance in the first year with beginning balance of $75 is $390.
Compare these two Ending balances using subtraction:
$390 – $338 = $52
The Ending balance in the second year with beginning balance of $25 is $663.52.
The Ending balance in the first year with begnining balance of $75 is $717.6.
Compare these two Ending balances using subtraction:
$717.6 – $663.52 = $54.08
The Ending balance in the third year with beginning balance of $25 is $1,002.06.
The Ending balance in the third year with beginning balance of $75 is $1,058.3.
Compare these two Ending balances using subtraction:
$1,058.3 – $1,002.06 = $56.24
Notice that the differences between Ending balances each year, from Exercise 13 and Exercise 14, are not the same and not $75.
Hence, the balance do not increase by $75 when the initial deposit increases by $75.
Question 15.
Account A and Account B both have a principal of $1,000 and an annual interest rate of 4%. No additional deposits or withdrawals are made. Account A earns simple interest. Account B earns interest compounded annually. Compare the amounts in the two accounts after 20 years. Which earns more interest? How much more?
Answer:
The account A earns simple interest, and account B earns interest compounded annually.
The principal for both accounts is $1,000.
Account A
Write interest rate as decimal. ie 4% = 0.04
Find the amount of interest earned in one year.
Principal × Interest rate = Interest in one year
$1,000 × 0.04 = $40
Now, find the amount of interest earned in 20 years.
Interest for 1 year × Number of years = Interest for 20 years
$40 × 20 = $800
Account A will earn $800 after 20 years.
Account B
Use the formula for compound interest compounded ‘manually.
A = P(1 + r)t
where P is the principal, r is interest rate(in decimal), t is the time in years and A is the amount in the account after t years if no withdrawals are made.
Find the final amount in the account after 10 years.
Substitute 20 for t, 1,000 for P and 0.04 for r in the formula.
A = 1,000(1 + 0.04)20
44 = 1,000(1.04)20
A = 1,000 ∙ 2.19
A = 2,190
The final amount iii account B is $2,190.
To find the amount of interest earned subtract principal from the final amount.
$2,190 – $1,000 = $1,190
Account C will earn $1,190 after 20 years.
Compare the amounts using subtraction:
$1,190 – $800 = $390
Account B will earn $390 more in compound interest after 20 years than account A earns in simple interest.
Account B will earn $390 more in compound interest after 20 years than account A earns in simple interest.
Texas Go Math Grade 7 Lesson 13.2 H.O.T. Focus on Higher Order Thinking Answer Key
Question 16.
Justify Reasoning Luisa deposited $2,000 in an account earning simple interest at an annual rate of 5%. She made no additional deposits and no withdrawals. When she closed the account, she had earned a total of $2,000 in interest. How long was the account open?
Answer:
The principal for Luis’s account is $2. 000.
Write interest rate as decimal. ie 5% 0.05
Find the amount of intere$ earned in one year.
Principal × Interest rate = Interest in one year
$2 000 × 0.05 = $100
We know that she earned a total of $2,000 in interest when she closed the account.
To find the number of years the account was open. we have to divide the total of interest earned by interest earned in one year.
\(\frac{\$ 2,000}{\$ 100}\) = 200
20 years the account was open.
Question 17.
Draw Conclusions Amanda deposits $500 into a savings account earning simple interest at an annual rate of 8%. Tori deposits $1,000 into a savings account earning simple interest at an annual rate of 2.5%. Neither girl makes any additional deposits or withdrawals. Which girl’s account will reach a balance of $1,500 first? Justify your answer.
Answer:
The principal for Anianda’s account is $500.
Write interest rate as decimal, ie 8% = 0.08
Find the amount of interest in one year.
Principal × Interest rate = Interest in one year
$500 × 0.08 = $40
The amount of interest in one year is $40.
We want to know when the total balance of Amanda’s account will be $1,500, ie how much interest the account needs to earn.
When we sum the principal and the total interest earned we get the total account balance.
Total balance = The principal + The total interest earned
$1,500 = $500 + The total interest earned
The total interest earned = $1,500 – $500 = $1,000
The total interest account needs to earn is $1,000.
As the account earns $40 for one year. how many years does it take for the account to earn $1,000?
To find the number of years needed divide the total interest by the interest in one year.
\(\frac{\$ 1,000}{\$ 40}\) = 2o
It needs 25 year to Amanda’s account reach a balance of $1,500.
The principal for Tori’s account is $1,000.
Write interest rate as decimal. ie 2.5% = 0.025
Find the amount of interest earn in one year.
Principal × Interest rate = Interest in one year
$1.000 × 0.025 = $25
The amount of interest earn in one year is $25.
We want to know when the total balance of Tori’s account will be $1,500, ie how much interest the account needs to earn.
When we sum the principal and the total interest earned we get the total account balance.
Total balance = The principal + The total interest earned
$1, 500 = $1,000 + The total interest earned
The total interest earned = $1,500 – $1,000 = $500
The total interest account needs to earn is $500.
As the account earns $25 for one year, how many years does it take for the account to earn $500?
To find the number of years needed divide the total interest by the interest in one year.
\(\frac{\$ 500}{\$ 25}\) = 20
It needs 20 year to Tori’s account reach a balance of $1,500.
Hence, Tori account will first reach a balance of $1,500.
Question 18.
Persevere in Problem Solving Gary invested $1,000 in an account earning interest at an annual rate of 5% compounded annually. Each year, he deposited an additional $1,000, and made no withdrawals. When he closed the account, he had a balance of $4,525.64. Make a table similar to the one in Example 2 to help you estimate how long the money was in the account. How much interest would Gary earn in that same time if he invests $10,000 and deposits $10,000 into the account each year?
Answer:

Each year Gary deposit $1,000 which represents the amount deposited for each year.
Amount of interest earned = New balance × Interest rate
Ending balance = New balance + Amount of interest earned
Write the interest rate as decimal. ie 5% = 0.05.
Year 1
New balance in the first year is $1,000.
Amount of interest earned = $1, 000 × 0.05 = $50
Ending balance = $1,000 + $50 = $1,050
Year 2
New balance in the second year is the Ending balance from previous year plus Amount deposited, ie $1,050+ $1,000 = $2,050
Amount of interest earned = $2,050 × 0.05 = $102.5
Ending balance = $2,050 + $102.5 = $2,152.50
Year 3
New balance in the third year is the Ending baIance from previous year plus Amount deposited, ie $2,152.50 + $1,000 = $3,152.5
Amount of interest earned = $3,152.5 × 0.5 = $157.63
Ending balance = $3,152.5 + $157.63 = $3,310.13
Year 4
New balance in the forth year is the Ending balance from previous year pLus Amount deposited, ie
$3,310.13 + $1,000 = $4,310.13
Amount of interest earned = $4, 310.13 × 0.5 = $215.51
Ending balance = $4,310.13 + $215.51 = $4,525.64
The money was 4 years in the account
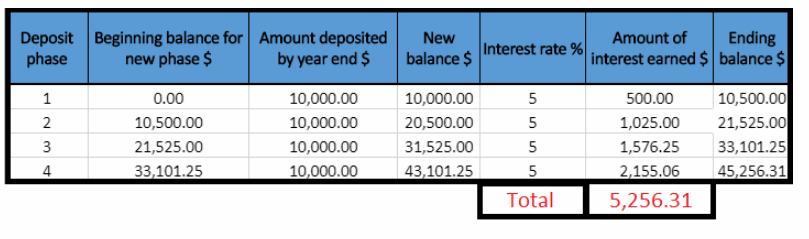
Each year Gary deposit $10,000 which represents the amount deposited for each year.
Amount of interest earned = New balance × Interest rate
Ending balance = New balance + Amount of interest earned
Wite the interest rate as decinial. ie 5% = 0.05.
Year 1
New balance in the first year is $10,000.
Amount of interest earned = $10,000 × 0.05 = $500
Ending balance = $10,000 + $500 = $10,500
Year 2
New balance in the second year is the Ending balance from previous year plus Amount deposited, ie
$10,500 + $10,000 = $20,500
Amount of interest earned = $20, 500 × 0.05 = $1,025
Ending balance = $20,500 + $1,025 = $21, 525
Year 3
New balance in the third year is the Ending balance from previous year plus Amount deposited, ie
$21,525 + $10,000 = $31,525
Amount of interest earned = $31,525 × 0.5 = $1,576.25
Ending balance = $31, 525 + $1, 576.25 = $33,101.25
Year 4
New balance in the forth year is the Eìiding balance from previous year plus Amount deposited. ie
$33,101.25 + $10,000 = $13, 101.25
Amount of interest earned = $43,101.25 × 0.5 = $2,155.06
Ending balance = $43,101.25 + $2,155.06 = $45,256.31
After 4 years Gary would earn interest of $5,256.31.
The money was 4 years in the account.
If Gary deposit $10,000 instead $1,000 he would earn interest of $5,256.31.
Check More: