Refer to our Texas Go Math Grade 7 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 7 Lesson 10.1 Answer Key Volume of Rectangular Prisms and Pyramids.
Texas Go Math Grade 7 Lesson 10.1 Answer Key Volume of Rectangular Prisms and Pyramids
Texas Go Math Grade 7 Lesson 10.1 Example Answer Key
Example 1.
Find the volume of the rectangular prism.
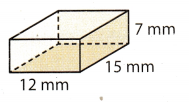
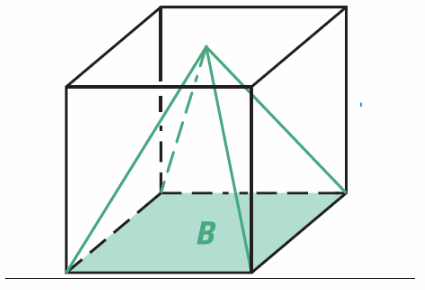
Step 1
Find the area of the base.
B = lw Use the formula.
B = 12 × 15 Substitute for l and w.
B = 180 mm2
Step 2
Find the volume.
V= Bh Use the formula.
V = 180 × 7 Substitute for sand h.
V = 1,1260 mm3
The volume of the rectangular prism is 1,260 cubic millimeters.
Reflect
Question 1.
What If? If you know the volume V and the height h of a prism, how would you find the area of the base B?
Answer:
The volume V of a prism is the area of its base B times its height h.
V = B.h…(1)
We know the volume V and the height of a prism.
Divide (1) by h.
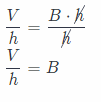
We find the area of the base B as \(\frac{V}{h}\) = B
Your Turn
Question 2.
Use the formula V = Bh to find the volume of a gift box that is 3.5 inches high, 7 inches long, and 6 inches wide.
Answer:
The volume V of a prism is the area of its base B times its height h.
V = B . h The volume of a prism
h = 3.5 Height of a prism
w = 6 Width of base
l = 7 Lenght of base
Find the area of the base.
B = w . l = 6 . 7 = 42 in2
Find the volume.
V = B . h = 42 . (3.5) = 147 m3
The volume V of a prism is V = 147 in3.
Texas Go Math Grade 7 Lesson 10.1 Explore Activity Answer Key
Nets
A net is a two-dimensional pattern of shapes that can be folded into a three-dimensional figure. The shapes in the net become the faces of the three-dimensional figure.
Step 1
Copy Net A and Ñet B on graph paper, and cut them out along the blue lines.
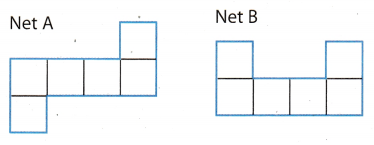
One of these nets can be folded along the black lines to make a cube. Which net will not make a cube? _________________
Step 2
See if you can find another net that can be folded into a cube.
Draw a net that you think will make a cube on your graph paper, and then cut it out. Can you fold it into a cube? Sketch your net below.
Step 3
Compare your results with several of your classmates. How many different nets for a cube did you and your classmates find?
Reflect
Question 3.
What shapes will appear in a net for a rectangular prism that is not a cube? How many of these shapes will there be?
Answer:
A rectangular prism is a three-dimensional shape with six rectangular shaped sides, so will appear six rectangles.
How do you know that each net cannot be folded into a cube without actually cutting and folding it?
Question 4.
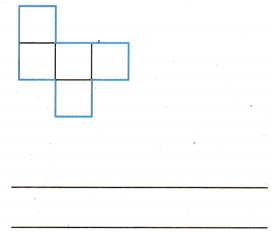
Answer:
This net cannot be folded in the shape of a cube because a cube is a three-dimensional figure with six equal square faces. The net is missing one square
Question 5.
Answer:
This net cannot be folded in the shape of a cube because a cube is a three-dimensional figure with six equal square faces. In this net the squares overlap.
Question 6.
Make a Conjecture If you draw a net for a cylinder, such as a soup can, how many two-dimensional geometric shapes would this net have? Name the shapes in the net for a cylinder.
Answer:
It will be three two-dimensional shapes; one rectangle and two circles
Exploring the Volume of a Rectangular Pyramid
A pyramid is a three-dimensional shape whose base is a polygon and whose other faces are all triangles. Like a prism, a pyramid is named by the shape of its base.
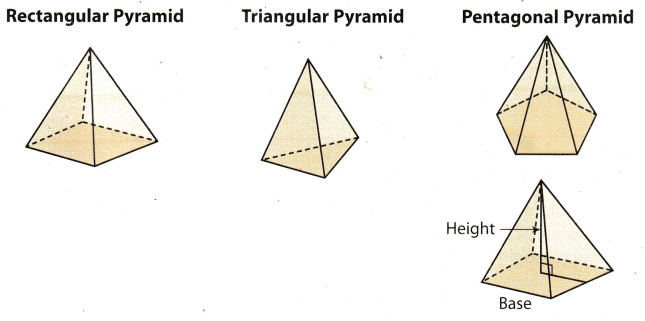
The faces of a pyramid that are not the base have a common vertex, called the vertex of the pyramid. The perpendicular distance from the vertex to the base is the height of the pyramid.
Explore Activity 2
In this activity, you will compare the volumes of a pyramid and a prism with congruent bases and equal heights. Remember that congruent figures have the same shape and size.
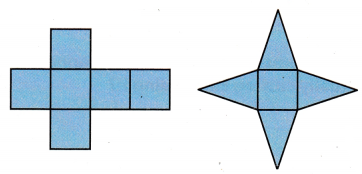
Step 1
Make three-dimensional models. Make larger versions of the nets shown. Make sure the bases and heights in each net are the same size. Fold each net, and tape it together to form a prism or a pyramid.
Step 2
Fill the pyramid with beans. Make sure that the beans are level with the opening of the pyramid. Then pour the beans into the prism. Repeat until the prism is full. How many times did you fill the prism from the pyramid? __________________________

Step 3
Write a fraction that compares the volume of the pyramid to the volume of the prism.
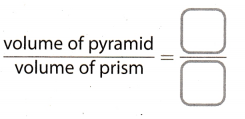
Math Talk
Mathematical Processes
Describe ways in which a prism and a pyramid are different.
Reflect
Question 7.
Draw Conclusions A rectangular pyramid has a base of B and a height of h. What is a formula for the volume of the pyramid? Justify your reasoning.
Answer:
Given base area of the rectangular Pyramid = B
Given height of the rectangular Pyramid = h
Volume of rectangular pyramid is the one-third of the base area times the height of pyramid.
Volume of rectangular pyramid = \(\frac{1}{3}\)Bh
Hence, volume of the rectangular pyramid is \(\frac{1}{3}\)Bh
volume of the rectangular pyramid is \(\frac{1}{3}\)Bh.
Question 8.
Communicate Mathematical Ideas The prism and the pyramid in this activity have congruent bases and equal heights. Are they congruent three-dimensional shapes? Explain.
Answer:
The prism and pyramid cannot be considered as congruent three-dimensional shapes even if they have the same
bases and equal heights. This is because their volumes are different. When a prism and pyramid have the congruent bases and equal heights, the prism will have a greater volume than the pyramid. This is basically, the pyramid can fit inside the prism. The volume of the pyramid is only \(\frac{1}{3}\) of the volume of the prism.
No
Your Turn
Question 9.
Thé volume of a rectangular prism is 4\(\frac{1}{2}\) in3. What is the volume of a rectangular pyramid with a congruent base and the same height? Explain your reasoning.
Answer:
ragged right The volume of a rectangular prism is:
V = B . h (1)
The volume of a rectangular pyramid is:
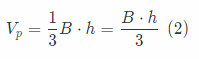
They have congruent base and same height
Divide (1) by 3
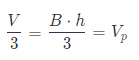
The volume of a rectangular pyramid is three time less than the volume of a rectangular prism
The volume of a rectangular pyramid is:
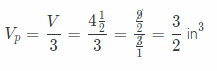
The volume of a rectangular pyramid is three time less than the volume of a rectangular prism.
VP = \(\frac{3}{2}\)in3
Solving Volume Problems
You can use the formulas for the volume of a rectangular prism and the volume of a rectangular pyramid to solve problems.
Volume of a Rectangular Pyramid
The volume V of a pyramid is one-third the area of its base B times its height h.
V = \(\frac{1}{3}\)Bh
Example 2
‘A Kyle needs to build a crate in the shape of a rectangular prism. The crate must have a volume of 38\(\frac{1}{2}\) cubic feet, and a base area of 15\(\frac{2}{3}\) square feet. Find the height of the crate.
V= Bh Use the formula.
38\(\frac{1}{2}\) = 15\(\frac{2}{5}\) . h Substitute for V and B.
\(\frac{77}{2}\) = \(\frac{77}{5}\)h Change the mixed numbers to fractions.
\(\frac{5}{77}\) . \(\frac{77}{2}\) = \(\frac{77}{5}\)h . \(\frac{5}{77}\) To divide both sides by \(\frac{77}{5}\), multiply both sides by the reciprocal.
\(\frac{5}{2}\) = h
The height of the crate must be \(\frac{5}{2}\) or 2\(\frac{1}{2}\), feet.
B. A glass paperweight in the shape of a rectangular pyramid has a base that is 4 inches by 3 inches and a height of 5 inches. Find the volume of the paperweight.
V= \(\frac{1}{3}\)Bh Use the formula.
V = \(\frac{1}{3}\) . 12 . 5 Think B = lw = 4 . 3 = 12
V = 20
The paperweight has a volume of 20 cubic inches.
Your Turn
Question 10.
A rectangular prism has a volume of 160 cubic centimeters and a height of 4 centimeters. What is the area of its base? _______
Answer:
V = B . h … (1)
V = 160 cm3 The volume of a prism
h = 4 cm Height of a prism
Divide (1) by h = 4
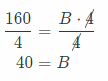
The area of the base is B = 40 cm2.
Question 11.
A square pyramid has a base edge’of 5.5 yards and a height of 3.25 yards. Find the volume of the pyramid to the nearest tenth. _______
Answer:
V = \(\frac{1}{3} B \cdot h\)
l = 5.5 yd Edge of base
h = 3.2 yd Height of pyramid
Find the base of a pyramid
B = (5.5). (5.5) = 30.25 yd2
Find the volume of a pyramid.
V = B . h = (30.25) . (3.25) = 98.3215 ≈ 98.3 yd3
The volume of a pyramid is V = 98.3 yd3.
Texas Go Math Grade 7 Lesson 10.1 Guided Practice Answer Key
Question 1.
Find the volume of the rectangular prism. (Example 1)
V = Bh
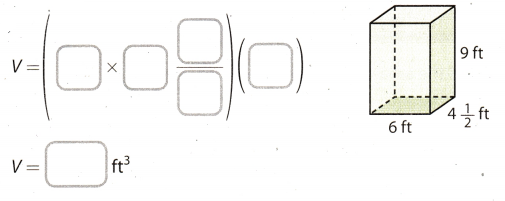
Answer:
l = 6ft Length ofabase
w = 4\(\frac{1}{2}\) ft Width of a base
h = 9 ft Height of a prism
The volume of a prism:
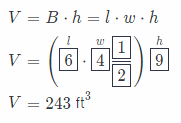
V = 243 ft3
Identify the three-dimensional shape that can be formed from each net.
(Explore Activity 1 and Explore Activity 2)
Question 2.
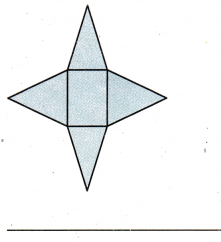
Answer:
The three-dimensional shape that can be formed from the given net is Rectangular Pyramid. Because the in given
net all the four side have triangular shape and the base is of rectangular shape.
Question 3.
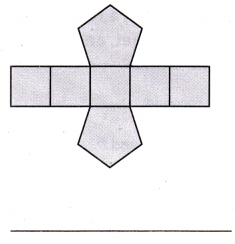
Answer:
The three-dimensional shape that can be formed from the given net is Pentagonal Prism. Because the in given net
all the four side and base have rectangular shape and front and behind of the prism is of pentagonal shape.
The three-dimensional shape that will be formed for the net ¡s also called as Heptahedron.
Question 4.
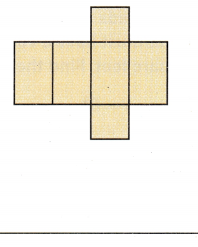
Answer:
The three-dimensional shape that can be formed from the given net is Rectangular Prism. Because the in given net all the four side have rectangular shape and the base and top of the prism is of square shape.
The three-dimensional shape that will be formed for the net is also called as cuboid.
Question 5.
The volume of a rectangular prism is 161.2 m3. The prism has a base that is 5.2 m by 3.1 m. Find the height of the prism. (Example 2)
Answer:
B = l . w Base of prism
l = 5.2 m Length of base
w = 3.1 m Width of base
h = ? Height of a prism
V = 161.2 m3 The volume of a prism
Use the formula B = l . w to find a base.
B = l . w = (5.2). (3.1) = 16.12 m2
Use the formula for the volume of a prism to find the height of the prism.
V = l . w . h

The height of the prism is h = 10 m.
Essential Question Check-In
Question 6.
Explain how to use models to show the relationship between the volume of a rectangular prism and a rectangular pyramid with congruent bases and heights.
Answer:
When you have a rectangular prism and rectangular pyramid with congruent bases and heights, you would notice that the rectangular pyramid can fit in the rectangular prism and there is still available space. This is because the prism will have a greater volume compared to the pyramid. Let’s say, that the rectangular prism will be filled with stones. The stones from the rectangular prism will be transferred to the rectangular pyramid notice that after the rectangular pyramid will be filled with stones and there are still remaining stones in the rectangular prism. This is because the volume of the rectangular pyramid is only \(\frac{1}{3}\) of the volume of the rectangular prism.
The relationship between a rectangular prism and rectangular pyramid with congruent bases and heights.
Texas Go Math Grade 7 Lesson 10.1 Independent Practice Answer Key
Question 8.
Explain the Error A student found the volume of a rectangular pyramid with a base area of 92 square meters and a height of 54 meters to be 4,968 cubic meters. Explain and correct the error.
Answer:
Error in this conclusion is:
A student used formula for the volume of a prism (V = B . h), not for the volume of a pyramid (VP = \(\frac{1}{3}\) . B. h).
That mistake can be corrected when the result divided with 3.
V = \(\frac{1}{3}\)B . h = \(\frac{1}{3}\) . 92 . 54 = \(\frac{1}{3}\) . 4968 = 1656
Error in this conclusion is:
A student used formula for the volume of a prism, not for the volume of a pyramid.
That mistake can be corrected when the result divided with 3.
Question 9.
A block of marble is in the shape of a rectangular prism. The block is 3 feet long, 2 feet wide, and 18 inches high. What is the volume of the block? _________________
Answer:
l = 3 ft Length of base
w = 2 ft Width of base
h = 1.5 ft Height of a prism
Use the formula B = l . w to find the base.
B = l . w = 3 . 2 = 6 ft2
Use the formula for the volume of a prism.
V = B . h
V = 6. (1.5)
V = 9 ft3
The volume of the block is V = 9 ft3.
Question 10.
Multistep Curtis builds a doghouse with base shaped like a cube and a roof shaped like a pyramid. The cube has an edge length of 3\(\frac{1}{2}\) feet.The height of the pyramid is 5 feet. Find the volume of the doghouse rounded to the nearest tenth.
Answer:
Base of doghouse is in the shape of a rectangular prism.
b = 3\(\frac{1}{2}\) = \(\frac{7}{2}\) ft Length of the base
h = \(\frac{7}{2}\)ft Height of a prism
Use the formula for the volume of a rectangular prism.
V1 = b . b . h
= \(\frac{7}{2}\) . \(\frac{7}{2}\) . \(\frac{7}{2}\)
= \(\frac{343}{8}\) ft3
The roof of a doghouse is in the shape of rectangular pyramid.
b = \(\frac{7}{2}\) ft Length of the base
h = 5 ft Height of a pyramid
Use the formula for the volume of a rectangular pyramid.
V2 = \(\frac{1}{3}\) . b . b . h
= \(\frac{1}{3}\) . \(\frac{7}{2}\) . \(\frac{7}{2}\) . 5
= \(\frac{245}{12}\) ft3
The volume of the doghouse is:
V = V1 + V2 = \(\frac{343}{8}\) . \(\frac{245}{12}\) = (42.875) + (20.416) ≈ 63.3 ft3
The Volume of the doghouse is V = 63.3 ft3
Question 11.
Miguel has an aquarium in the shape of a rectangular prism. The base is 30.25 inches long and 12.5 inches wide. The aquarium is 12.75 inches high. What is the volume of the aquarium to the nearest cubic inch?
Answer:
l = 30.25 in length of base
w = 12.5 in Width of base
h = 12.75 in Height of a prism
Use the formula B = l . w to find a base.
B = l . w = (30.25). (12.5) = 378.125 in2
Use the formula for the volume of a prism.
V = B . h.
= (378.125) . (12.75)
= 4, 821.09375 ≈ 4,821.09 in3
The volume of the aquarium is V = 4,821.09 in3.
Question 12.
After a snowfall, Sheree built a snow pyramid. The pyramid had a square base with side lengths of 32 inches and a height of 28 inches. What was the volume of the pyramid to the nearest cubic inch?
Answer:
b = 32 in length of base
h = 28 in Height of a pyramid
Use the formula
B = b. b to find the base.
B = b . b = 32 . 32 = 1024 in2
Use the formula for the volume of a pyramid.
V = \(\frac{1}{3}\) . B . h
= \(\frac{1}{3}\) . 1024. 28
= \(\frac{1024.28}{3}\)
= 9, 557.333 ≈ 9, 557.3 in3
The volume of the pyramid is V = 9, 557.3 in3.
Question 13.
A storage chest has the shape of a rectangular prism with the dimensions shown. The volume of the storage chest is
18,432 cubic inches. What is its height?
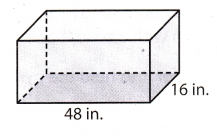
Answer:
V = 18, 432 in3 The volume of the storage chest
l = 48 in Length of a base
w = 16m Width of a base
B = l . w = 48 . 16 = 768 m2 Base area of a prism
The storage chest has a shape of a prism. Use formula for the volume of a prism and subtitute values for B and h.
V = B . h
18432 = 768 . h
Divide by 768 both sides.
\(\frac{18432}{768}\) = h
24 = h
The height of the storage chest is 24 in.
Question 14.
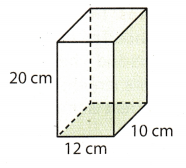
Draw Conclusions A shipping company ships certain boxes at a special rate. The boxes must not have a volume greater than 2,500 cm3. Can the box shown be shipped at the special rate? Explain.
Answer:
Length of the given box = 10 cm
Width of the given box = 12 cm
H eight of the given box = 20 cm
We know that volume of box is = Length × width × height
VoLume of box = 10 × 12 × 20 cm3
= 2400 cm3
It is given in the problem that shipping company ships certain boxes at special rate only if the volume of box is not greater than 2, 500 cm3 And the volume of the given box is 2, 400 cm3. So the box will be shipped at special rate by shipping company.
Yes, the box will be shipped at special rate.
Yes, the box will be shipped at special rate.
Question 15.
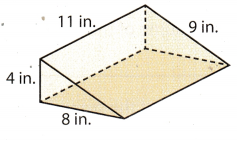
Communicate Mathematical Ideas Is the figure shown a prism or a pyramid? Justify your answer.
Answer:
Given figure is triangular Prism
Because prism is a figure which has parallel top and bottom bases. And pyramid has a base and triangular faces
which meet at common vertex point. In the given figure we can see that both triangle faces are parallel to each
other which has base length of 8 inch and height of 4 inch.
Question 16.
A cereal box can hold 144 cubic inches of cereal. Suppose the box is 8 inches long and 1.5 inches wide. How tall is the box?
Answer:
The cereal box is in the shape of rectangular prism.
l = 8 in Length of base
w = 1.5 in Width of base
h = ? Height of a prism
V = 144 in3 The volume of a prism
Use the formula B = l . w to find the base.
B = l . w = 8 . (1.5) = 12 in2
Use the formula for the volume of a prism to find the height of the prism.
V = B . h
144 = 12 . h
Divide both sides by 12.
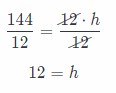
The box is 12 in. tall.
Question 17.
A Shed in the shape of a rectangular prism has a volume of 1,080 cubic feet. The height of the shed is 8 feet, and the width of its base is 9 feet. What is the length of the shed?
Answer:
V = 1080 ft3 The volume of a rectangular prism
h = 8 ft Length of prism
l = ? Length of base
w = 9 ft Width of base
Use the formula for the volume of a prism to find a length of the base.
V = l . w . h.
1080 = l . 9 . 8
1080 = l . 72
Divide both sides by 72.
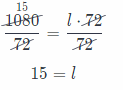
The length of shed is 15 ft.
H.O.T. Focus on Higher Order Thinking
Question 18.
Draw Conclusions Sue has a plastic paperweight shaped like a rectangular pyramid. The volume is 120 cubic inches, the height is 6 inches, and the length is 10 inches. She has a gift box that is a rectangular prism with a base that is 6 inches by 10 inches. How tall must the box be for it to hold the pyramid?
Answer:
Given volume of pyramid = 120 inch3
Height of pyramid = 6 inch
Length of pyramid = 10 inch
Volume of pyramid = \(\frac{\text { length } \times \text { width } \times \text { height }}{3}\)
120 = \(\frac{10 \times \text { width } \times 6}{3}\)
width = \(\frac{120 \times 3}{10 \times 6}\)
width = 6 inch
So, base of the pyramid is 6 inch by 10 inch and also the base of prism (box) is 6 inch by 10 inch. This means the height of pyramid to fit in completely but the volume of prism or box will be 3 times the volume of pyramid.
Hence, the box must be 6 inch tall to hold the pyramid.
This can be best understood by the given below figure in which pyramid is inside the prism with both having same base area.
Required height is 6 inch.
Question 19.
Represent Real-World Problems A public swimming pool is in the shape of a rectangular prism. The pool is 20 meters long and 16 meters wide. The pool is filled to a depth of 1.75 meters.
a. Find the volume of water in the pool.
h = 1.75 m Height of prism
l = 20 m Length of base
w = 16 m Width of base
Use the formula for the volume of a rectangular prism.
V = l . w . h
= 20 . 16 . (1.75)
= 320 . (1.75)
= 560 m3
The volume of water in the pool is 560 m3.
b. A cubic meter of water has a mass of 1,000 kilograms. Find the mass of the water in the pool.
Answer:
Mass of the water in the pool is:
560 . 1000 = 560,000 kg
The mass of the water in the pool is 560, 000 kg.
Question 20.
Analyze Relationships There are two glass pyramids at the Louvre Museum in Paris, France. The outdoor pyramid has a square base with side lengths of 35.4 meters and a height of 21.6 meters. The indoor pyramid has a square base with side lengths of 15.5 meters and a height of 7 meters. How many times as great is the volume of the outdoor pyramid than that of the indoor pyramid?
Answer:
The outdoor pyramid is in the shape of a rectangular pyramid.
b = 35.4 m Length of the base
h = 21.6 m Height of a pyramid
Use the formula for the volume of a rectangular pyramid.
V1 = \(\frac{1}{3}\) . b . b . h
= \(\frac{1}{3}\)(35.4). (35.4). (21.6)
= 9,022.752 m3
The indoor pyramid is in the shape of rectangular pyramid.
b = 15.5 m Length of the base
h = 7 m Height of a pyramid
Use the formula for the volume of a rectangular pyramid.
V2 = \(\frac{1}{3}\) . b . b . h
= \(\frac{1}{3}\) . (15.5) . (15.5) . 7
= 560.583 m3
\(\frac{V_{1}}{V_{2}}\) = \(\frac{9022.752}{560.583}\) = 16.095 ≈ 16
The volume of the outdoor pyramid is 16 times greater then the volume of the indoor pyramid.
Question 21.
Persevere in Problem Solving A small solid pyramid was installed on top of the Washington Monument in 1884. The square base of the pyramid is 13.9 centimeters on a side, and the height of the pyramid is 22.6 centimeters. The pyramid has a mass of 2.85 kilograms.
a. Find the volume of the pyramid. Round to the nearest hundredth.
Answer:
b = 13.9 cm length of the base
h = 22.6 cm Height of a pyramid
Use the formula for the volume of a rectangular pyramid
V1 = \(\frac{1}{3}\) . b . b . h
= \(\frac{1}{3}\) . (13.9) . (13.9). (22.6)
= 1455.51 cm3
a. The volume of the pyramid is:
V = 1455.51 ≈ 1456 cm3
b. Find the mass of the pyramid in grams.
Answer:
The pyramid has mass of 285 kg. There are 1000 grams in 1 kilogram. Mass of the pyramid in grams is: 2.85 .
1000 = 2850 gr.
c. Science The density of a substance is the ratio of its mass to its volume. Find the density of the pyramid in grams per cubic centimeter. Round to the nearest hundredth.
Answer:
The density of the pyramid is \(\frac{\text { Mass }}{\text { Volume }}\) = \(\frac{2850}{1456}\) ≈ 2g/cm3.