Refer to our Texas Go Math Grade 7 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 7 Lesson 1.4 Answer Key Subtracting Rational Numbers.
Texas Go Math Grade 7 Lesson 1.4 Answer Key Subtracting Rational Numbers
Example 1
The temperature on an outdoor thermometer on Monday was 5.5 °C. The temperature on Thursday was 7.25 degrees less than the temperature on Monday. What was the temperature on Thursday?
Answer:
Subtract to find the temperature on Thursday.
Step 1: Find 5.5 – 7.25
Step 2: Start at 5.5

Step 3: Move |7.25| = 7.25 units to the left because you are subtracting a positive number.
The result is -1.75
The temperature on Thursday was -1.75 °C.
Your Turn
Use a number line to find each difference.
Question 1.
-6.5 – 2 = __________
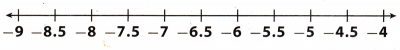
Answer:
Start at -6.5.
Move |2| = 2 units to the left because you are subtracting a positive number
The result is -8.5.

Question 2.
1\(\frac{1}{2}\) – 2 = __________
![]()
Answer:
Start at 1\(\frac{1}{2}\).
Move |2| = 2 units to the left because you are subtracting a positive number
The result is -0.5.

Question 3.
-2.25 – 5.5 = __________
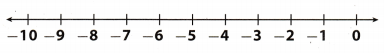
Answer:
Start at -2.25.
Move |5.5| = 5.5 units to the left because you are subtracting a positive number
The result is -7.75.

Example 2
During the hottest week of the summer, the water level of the Muskrat River was \(\frac{5}{6}\) foot below normal. The following week, the level was foot below normal. What is the overall change in the water level?
Answer:
Subtract to find the difference in water levels.
Step 1: Find –\(\frac{1}{3}\) – (-\(\frac{5}{6}\)).
Step 2: Start at –\(\frac{1}{3}\).

Step 3: Move |-\(\frac{5}{6}\)| = \(\frac{5}{6}\) to the right because you are subtracting a negative number.
The result is \(\frac{1}{2}\).
So, the water level increased \(\frac{1}{2}\) foot.
Reflect
Question 4.
Work with other students to compare addition of negative numbers on a number line to subtraction of negative numbers on a number line.
Answer:
We conclude that when it comes to addition of negative numbers we move to the left, while we move to the right in subtraction of negative numbers.
Question 5.
Compare the methods used to solve Example 1 and Example 2.
Answer:
Methods are the same, in both we use subtraction, the difference is in moving left (example 1) or right (example 2) on the number tine, and that depends on the subtrahend, whether it is positive or negative.
Your Turn
Use a number line to find each difference.
Question 6.
0.25 – (-1.50) = ___________

Answer:
Start at 0.25.
Move |-1.50| = 1.50 units to the right because you are subtracting a positive number
The result is 1.75.

Question 7.
– \(\frac{1}{2}\) – (-\(\frac{3}{4}\)) = ____________
![]()
Answer:
Step 1
Start at –\(\frac{1}{2}\)
Move |-\(\frac{3}{4}\)| = \(\frac{3}{4}\) units to the right because you are subtracting a negative number
The result is \(\frac{1}{4}\)

Explore Activity 1
Adding the Opposite
Joe is diving 2\(\frac{1}{2}\) feet below sea level. He decides to descend 7\(\frac{1}{2}\) more feet. How many feet below sea level is he?
Answer:
Step 1: Use negative numbers to represent the number of feet below sea level.
Step 2: Find -2\(\frac{1}{2}\) – 7\(\frac{1}{2}\).
Step 3: Start at -2\(\frac{1}{2}\).
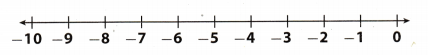
Step 4: Move |7\(\frac{1}{2}\)| = 7\(\frac{1}{2}\) units to the _____________________
because you are subtracting a ____________________ number.
The result is -10.
Joe is ______________________ sea level.
Reflect
Question 8.
Use a number line to find each difference or sum.
a. -3 – 3 = __________
![]()
Answer:
Start at -3.
Move |3| = 3 units to the left because you are subtracting a positive number.
The result is -6.
b. -3 + (-3) = __________
![]()
Answer:
Start at -3.
Move |-3| = 3 units to the left because you are subtracting a positive number.
The result is -6.

Question 9.
Make a Conjecture Work with other students to make a conjecture about how to change a subtraction problem into an addition problem.
Answer:
We conclude that we can substitute a subtraction problem with an addition problem. Minuend becomes the
first addend, while the second addend is a negative subtrahend
E.g.
5 – 3 = 5 + (-3)
Explore Activity 2
A cave explorer climbed from an elevation of -11 meters to an elevation of -5 meters. What vertical distance did the explorer climb?
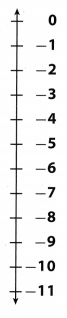
There are two ways to find the vertical distance.
A.
Start at ________.
Count the number of units on the vertical number line up to -5.
The explorer climbed __________ meters.
This means that the vertical distance between
-11 meters and -5 meters is ________ meters.
B.
Find the difference between the two elevations and use absolute value to find the distance.
11 – (-5) = __________
Take the absolute value of the difference because distance traveled is always a nonnegative number.
|-11 -(-5)| = __________
The vertical distance is _________meters.
Reflect
Question 10.
Does it matter which way you subtract the values when finding distance? Explain.
Answer:
It does not matter, because the difference in two ways is in the sign (+/-) Thus, when we take the absolute values
of the results, it’s the same.
E.g.
5 – 3 = 2
|5 – 3| = 2
3 – 5 = -2
|3 – 5| = 2
Question 11.
Would the same methods work if both the numbers were positive? What if one of the numbers were positive and the other negative?
Answer:
Yes, it would still work if both the numbers were positive.
It would not make a difference if one of the numbers were positive and the other negative. We would still use the same method.
Texas Go Math Grade 7 Lesson 1.4 Guided Practice Answer Key
Use a number line to find each difference. (Example 1, Example 2 and Explore Activity 1)
Question 1.
5 – (-8) = ___________
![]()
Answer:
Start at 5.
Move |-8| = 8 units to the right because you are subtracting a negative number.
The result is 13.

Question 2.
-3\(\frac{1}{2}\) -4\(\frac{1}{2}\) = __________

Answer:
Start at -3\(\frac{1}{2}\).
Move |-4\(\frac{1}{2}\)| = 4\(\frac{1}{2}\) units to the left because you are subtracting a positive number
The result is -8

Question 3.
-7 – 4 = __________
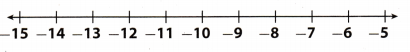
Answer:
Start at -7.
Move |4| = 4 units to the left because you are subtracting a positive number
The result is -11.

Question 4.
-0.5 – 3.5 = __________
![]()
Answer:
Start at -0.5.
Move |3.5| = 3.5 units to the left because you are subtracting a positive number
The result is -4.
Find each difference. (Explore Activity 1)
Question 5.
-14 – 22 = ___________
Answer:
– 36
Question 6.
-12.5 – (-4.5) = ________
Answer:
Start by changing subtraction problem to addition problem.
= -12.5 + 4.8
= -7.7
Question 7.
\(\frac{1}{3}\) – (-\(\frac{2}{3}\)) = ___________
Answer:
Start by changing subtraction problem to addition problem.
= \(\frac{1}{3}\) + \(\frac{2}{3}\)
= \(\frac{3}{3}\)
= 1
Question 8.
65 – (-14) = ___________
Answer:
Start by changing subtraction problem to addition problem.
= 65 + 14
= 79
Question 9.
–\(\frac{2}{9}\) – (-3) = _________
Answer:
Start by changing subtraction problem to addition problem.
= –\(\frac{2}{9}\) + 3
= 2\(\frac{7}{9}\)
Question 10.
24\(\frac{3}{8}\) – (-54\(\frac{1}{8}\)) = ___________
Answer:
Start by changing subtraction problem to addition problem.
= 24\(\frac{3}{8}\) + 54\(\frac{1}{8}\)
= 78\(\frac{4}{8}\)
(1) = 78\(\frac{1}{2}\)
(1) Cancel fraction.
Question 11.
A girl is snorkeling 1 meter below sea level and then dives down another 0.5 meter. How far below sea level is the girl? (Explore Activity 1)
Answer:
Use negative numbers to represent the number of feet below sea level
Find -1 – 0.5.
Start at -1.
Move |0.5| = 0.5 units to the left because you are subtracting a positive number
The result is -1.5. The girl is now 1.5 meters below sea level.

Question 12.
The first play of a football game resulted in a loss of 1 yards. Then a penalty resulted in another loss of 5 yards. What is the total loss or gain? (Explore Activity 1)
Answer:
Use negative numbers to represent the number of yards lost
Find -12\(\frac{1}{2}\) – 5.
Start at -12\(\frac{1}{2}\).
Move |5| = 5 units to the left because you are subtracting apositive number
The result is-17\(\frac{1}{2}\). Total loss is -17\(\frac{1}{2}\) yards.

Question 13.
A climber starts descending from 533 feet above sea level and keeps going until she reaches 10 feet below sea level. How many feet did she descend? (Explore Activity 2)
Answer:
Find the difference between the two heights and use absolute value to find the distance.
533 – (-10) = 533 + 10
= 543
Take the absolute value of the difference, because distance descended is always a posiùve number
|543| = 543
The climber descended 543 feet
Question 14.
Eleni withdrew $45.00 from her savings account. She then used her debit card to buy groceries for $30.15. What was the total amount Eleni took out of her account? (Explore Activity 1)
Answer:
Use negative numbers to represent the number of money withdrawn or spent.
Find -45 – 30,15.
Start at -45.
Move |30.15| = 30.15 units to the left because you are subtracting a positive number.
The result is -75.15. Eleni took total of $75.15 of her account.

Essential Question Check-In
Question 15.
Mandy is trying to subtract 4-12, and she has asked you for help. How would you explain the process of solving the problem to Mandy, using a number line?
Answer:
Start at 4
Move |12| = 12 units to the left because you are subtracting a positive number.
The resuLt is -8.

Texas Go Math Grade 7 Lesson 1.4 Independent Practice Answer Key
Question 16.
Science At the beginning of a laboratory experiment, the temperature of a substance is -12.6°C. During the experiment, the temperature of the substance decreases 7.5 °C. What is the final temperature of the substance?
Answer:
Subtract temperatures to find the final temperature of the substance.
Find -12.6 – 7.5.
Start at -12.6.
Move |7.5| = 7.5 units to the left because you are subtracting a positive number
The result is -20.1. Final temperature of the substance is -20.1°C

Question 17.
A diver went 25.65 feet below the surface of the ocean, and then 16.5 feet further down, he then rose 12.45 feet. Write and solve an expression to find the diver’s new depth.
Answer:
Find -25.65 – 16.5 – 12.45.
First find -25.65 – 16.5.
Start at – 25.65.
Move |16.5| = 16.5 units to the left because you are subtracting a positive number.
The result is -42.15.
Now find -42.15 + 12.45.
Start at -42.15.
Move |12.45| = 12.45 units to the right because you are adding a positive number.
The result is -29.7. Diver’s new depth is -29.7 feet.

Question 18.
A city known for its temperature extremes started the day at -5 degrees Fahrenheit. The temperature increased by 78 degrees Fahrenheit by midday, and then dropped 32 degrees by nightfall.
a. What expression can you write to find the temperature at nightfall?
Answer:
The temperature started the day at -5 degrees Fahrenheit, then it increased by 78 degrees That means we add 78 to -5. Lastly, the temperature dropped 32 degree& That means we subtract 32 from the result.
-5 + 78 – 32
b. What expression can you write to describe the overall change in temperature? Hint: Do not include the temperature at the beginning of the day since you only want to know about how much the temperature changed.
Answer:
Using the hint we see that we only need to use changes in temperatures. First change is -r78 degrees, and next is -32 degrees.
78 – 32
c. What is the final temperature at nightfall? What is the overall change in temperature?
Answer:
To get the final temperature we calculate expression from a).
-5 + 78 – 32 = 73 – 32
= 41
To get the overall change in temperature we calculate expression from b).
78 – 32 = 46
Question 19.
Financial Literacy On Monday, your bank account balance was -$12.58. Because you didn’t realize this, you wrote a check for $30.72 for groceries.
a. What is the new balance in your checking account?
Answer:
The balance was -$12.38. and a check was written on $30.72. That means we to subtract the amount written on the check from the balance.
– 12.58 – 30.72 = -43.3
New balance is – $43.3.
b. The bank charges a $25 fee for paying a check on a negative balance. What is the balance in your checking account after this fee?
Answer:
We have to subtract the fee from the new balance.
-43.3 – 25 = -68.3
Balance after fee is $68.3.
c. How much money do you need to deposit to bring your account balance back up to $0 after the fee?
Answer:
We have to deposit the opposite of the debt we have. That is $68.3.
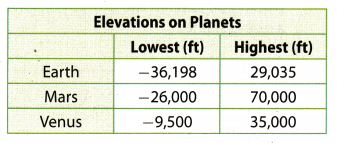
Astronomy Use the table for problems 20-21.

Question 20.
How much deeper is the deepest canyon on Mars than the deepest canyon on Venus?
Answer:
Deepest canyon on Mars is at -26000 feet
Deepest canyon on Venus is at -9500 feet
To calculate the difference we have to subtract these 2 numbers, and then take the absolute value of the result.
-26000 – (-9500) = -26000 + 9500
= -16500
|-16500| = 16500
Deepest canyon on Mars is 16500 feet deeper that the deepest canyon on Venus.
Question 21.
Persevere in Problem Solving What is the difference between Earth’s highest mountain and its deepest ocean canyon? What is the difference between Mars highest mountain and its deepest canyon? Which difference is greater? How much greater is it?
Answer:
To find the difference between the highest mountain and the deepest ocean canyon, we have to subtract mountain height from the ocean depth, and then take the absolute value of the result
Earth:
29035 – (-36198) = 29035 + 36198
= 65233
|65233| = 65233
Mars:
70000 – (-26000) = 70000 + 26000
= 96000
|96000| = 96000
We can see that 96000 > 65233. To calculate how much, subtract 65233 from 96000.
96000 – 65223 = 30777
Question 22.
Pamela wants to make some friendship bracelets for her friends. Each friendship bracelet needs 5.2 inches of string.
a. If Pamela has 20 inches of string, does she have enough to make bracelets for 4 of her friends?
Answer:
First we need to ca[cu[ate how much are 4 bracelets long. We need to add 5.2 inches 4 times.
5.2 + 5.2 + 5.2 + 5.2 = 10.4 + 5.2 + 5.2
= 15.6 + 5.2
= 20.8
Since, 20.8 is greater than 20, she will not have enough to make for all of her 4 friends.
b. If so, how much string would she have left over? If not, how much more string would she need?
Answer:
To calculate how much more string she would need, we need to substract the length of string she has from the
length of string she needs.
20.8 – 20 = 0.8
She needs 0.8 inches more.
Question 23.
Jeremy is practicing some tricks on his skateboard. One trick takes him forward 5 feet, then he flips around and moves backwards 7.2 feet, then he moves forward again for 2.2 feet.
a. What expression could be used to find how far Jeremy is from his starting position when he finishes the trick?
Answer:
If the first trick takes him forward 5 feet, that means he goes +5 feet forward. Second trick takes him 7.2 feet back, that means we subtract -7.2 from 5. Third trick moves him +2 feet forwards, that means we add 2 feet to
previous position.
5 – 7.2 + 2
b. How far from his starting point is he when he finishes the trick? Explain
Answer:
We have to calculate the expression from a), and then take its absolute value to find how far is he from his starting position after the trick.
5 – 7.2 + 2 = -2.2 + 2
= -0.2
|-0.2| = 0.2
He is 0.2 feet away from the starting position.
Question 24.
Esteban has $20 from his allowance. There is a comic book he wishes to buy that costs $4.25, a cereal bar that costs $0.89, and a small remote control car that costs $ 10.99.
a. Does Esteban have enough to buy everything?
Answer:
We have to add all of the expenses, and then check if they are greater than Esteban’s allowance to cheek if he has enough.
4.25 + 0.89 + 10.99 = 5.14 + 10.99
= 16.13
20 > 16.13
The allowance is greater than the expenses. Thus. Esteban has enough money to buy everything.
b. if so, how much will he have left over? If not, how much does he still need?
Answer:
To find out how much will he have leftover, we need to subtract the expenses from the allowance.
20 – 16.13 = 3.87
Esteban will have $3.87 leftover.
H.O.T. Focus on Higher Order Thinking
Question 25.
Look for a Pattern Show how you could use the Commutative Property to simplify the evaluation of the expression \(-\frac{7}{16}-\frac{1}{4}-\frac{5}{16}\)
Answer:
We can see that the first and the last member of the expression have the same denominator. Use the Commutative Property to switch second and third member. Now we have:
–\(\frac{7}{16}\) – \(\frac{5}{16}\) – \(\frac{1}{4}\)
Calculate the expression:
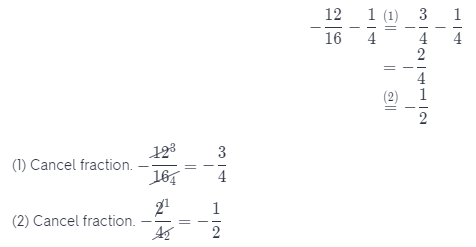
Question 26.
Problem Solving The temperatures for five days in Kaktovik, Alaska, are given below.
-19.6 °F, -22.5 °F, -20.9 °F, -19.5 °F, -22.4 °F
Temperatures over the same 5-day period last year were 12 degrees lower. What were the highest and lowest temperatures over this period last year?
Answer:
If all temperatures where 12 degrees lower last year, then the highest/lowest temperature last year will be on the same day as the highest/Lowest temperature this year.
We can see that the lowest temperature this year is on the second day: -22.5° F, and that the highest temperature is on the fourth day: -19.5° F.
Since last year all temperatures were 12 degrees lower, we subtract 12 from highest/lowest temperature this year.
-22.5 – 12 = -34.5
-19.5 – 12 = -31.5
The lowest temperature last year was -34.5° F.
The highest temperature last year was -31.5° F.
Question 27.
Make a Conjecture Must the difference between two rational numbers be a rational number? Explain.
Answer:
Yes, it must be a rational number.
We know that when we need to subtract one rational number from another, we need to find a common denominator, and then subtract numerators
Thus, our result will be a fraction.
Thus, a rational number
Question 28.
Look for a Pattern Evan said that the difference between two negative numbers must be negative. Was he right? Use examples to illustrate your answer.
Answer:
No, he was not right.
E.g.
–\(\frac{1}{4}\) – (-\(\frac{2}{4}\)) = –\(\frac{1}{4}\) + \(\frac{2}{4}\)
= \(\frac{1}{4}\)
If both numbers are negative, but minuend is greater than the subtracted, we will get a positive number as a result.