Refer to our Texas Go Math Grade 7 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 7 Lesson 1.1 Answer Key Rational Numbers and Decimals.
Texas Go Math Grade 7 Lesson 1.1 Answer Key Rational Numbers and Decimals
Texas Go Math Grade 7 Lesson 1.1 Explore Activity Answer Key
A. Use a calculator to find the equivalent decimal form of each fraction. Remember that numbers that repeat can be written as 0.333… or 0.\(\overline{3}\).

B. Now find the corresponding fraction of the decimal equivalents given in the last two columns in the table. Write the fractions in simplest form.
C. Conjecture What do you notice about the digits after the decimal point in the decimal forms of the fractions? Compare notes with your neighbor and refine your conjecture if necessary.
Reflect
Question 1.
Consider the decimal 0.101001000100001000001…. Do you think this decimal represents a rational number? Why or why not?
Answer:
This decimal. number does not represent a rationaL number because it racks a repeating pattern.
Question 2.
Do you think a negative sign affects whether or not a number is a rational number? Use –\(\frac{8}{5}\) as an example.
Answer:
No, a negative sign does not affect whether or not a number is a rationaL number.
– \(\frac{8}{5}\) = \(\frac{-8}{5}\)
No, – \(\frac{8}{5}\) = \(\frac{-8}{5}\)
EXPLORE ACTIVITY (cont’d)
Question 3.
Do you think a mixed number is a rational number? Explain.
Answer:
Yes, a mixed number is a rational number because it can be written as a simpLe fraction.
For exampLe,
2 \(\frac{1}{4}\) = \(\frac{9}{4}\)
Your Turn
Write each rational number as a decimal.
Question 4.
\(\frac{4}{7}\) ___________
Answer:
Complete the long division.
Stop when you discover a pattern.
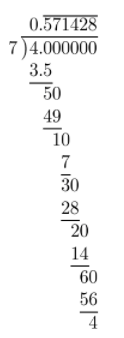
= \(0 . \overline{571428}\)
Question 5.
\(\frac{1}{3}\) ___________
Answer:
Complete the long division.
Stop when you discover a pattern.
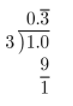
= \(0 . \overline{3}\)
Question 6.
\(\frac{9}{20}\) __________
Answer:
Complete the long division.

= 0.45
Question 7.
Yvonne made 2\(\frac{3}{4}\) quarts of punch. Write 2\(\frac{3}{4}\) as a decimal. 2\(\frac{3}{4}\) = _________ Is the decimal equivalent a terminating or repeating decimal
Answer:
First, write \(\frac{3}{4}\) as a decimal.
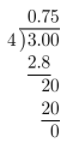
Then, add 2 to the result.
2 + 0.75 = 2.75
The decimal equivalent is a terminating decimal.
2.75, The decimal equivalent is a terminating decimal.
Question 8.
Yvonne bought a watermelon that weighed 7\(\frac{1}{3}\) pounds. Write 7\(\frac{1}{3}\) as a decimal. 7\(\frac{1}{3}\) = __________
Is the decimal equivalent a terminating or repeating decimal?
Answer:
First, write \(\frac{1}{3}\) as a decimal.
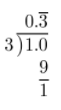
Then, add 7 to the result.
7 + \(0 . \overline{3}\) = \(7 . \overline{3}\)
The decimal equivalent is a terminating decimal.
\(7 . \overline{3}\) , The decimal equivalent is a repeating decimal.
Texas Go Math Grade 7 Lesson 1.1 Guided Practice Answer Key
Write each rational number as a decimal. Then tell whether each decimal is a terminating or a repeating decimal. (Explore Activity and Example 1)
Question 1.
\(\frac{3}{5}\) = ____________
Answer:
Complete the long division.
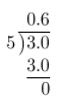
The decimal equivalent is a terminating decimal.
0.6; Terminating decimal.
Question 2.
\(\frac{89}{100}\) = _____________
Answer:
Complete the long division.
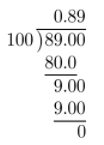
The decimal equivalent is a terminating decimal.
0.89; Terminating decimal.
Question 3.
\(\frac{4}{12}\) = ______________
Answer:
Complete the long division.
Stop when you discover a pattern.
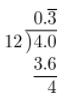
The decimal equivalent is a repeating decimal.
\(0 . \overline{3}\) ; Repeating decimal.
Question 4.
\(\frac{25}{99}\) = ______________
Answer:
Complete the long division.
Stop when you discover a pattern.
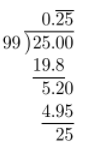
The decimal equivalent is a repeating decimal.
\(0 . \overline{25}\) ; Repeating decimal.
Question 5.
\(\frac{7}{9}\) = ____________
Answer:
Complete the long division.
Stop when you discover a pattern.
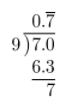
The decimal equivalent is a repeating decimal.
\(0 . \overline{7}\) ; Repeating decimal.
Question 6.
\(\frac{9}{25}\) = ____________
Answer:
Complete the long division.
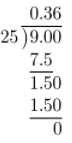
The decimal equivalent is a terminating decimal.
0.36; Terminating decimal.
Question 7.
\(\frac{1}{25}\) = ___________
Answer:
Complete the long division.
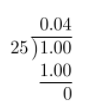
The decimal equivalent is a terminating decimal.
0.04; Terminating decimal.
Question 8.
\(\frac{25}{176}\) = ____________
Answer:
Complete long division.
Stop when you discover a pattern.
This case is special because the first. four decimal are not a part of the pattern that occurs after them.

The decimal equivalent is a repeating decimal.
\(0.1420 \overline{45}\) ; Repeating decimal.
Question 9.
\(\frac{12}{1,000}\) = _____________
Answer:
Complete the long division.

The decimal equivalent is a terminating decimal.
0.012; Terminating decimal.
Write each mixed number as a decimal. (Example 2)
Question 10.
11\(\frac{1}{6}\) = ___________
Answer:
First, write \(\frac{1}{6}\) as a decimal.
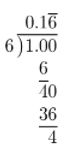
Then, add 11 to the result.
11 + \(0.1 \overline{6}\) = \(11.1 \overline{6}\)
= \(11.1 \overline{6}\)
Question 11.
2\(\frac{9}{10}\) = ____________
Answer:
First, write \(\frac{9}{10}\) as a decimal.
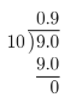
Then, add 2 to the result.
2 + 0.9 = 2.9
= 2.9
Question 12.
8\(\frac{23}{100}\) = _____________
Answer:
First, write \(\frac{23}{100}\) as a decimal.
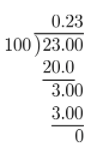
Then, add 8 to the result.
8 + 0.23 = 8.23
8.23
Question 13.
7\(\frac{3}{15}\) = ___________
Answer:
First, write \(\frac{3}{15}\) as a decimal.
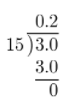
Then, add 7 to the result.
7 + 0.2 = 7.2
= 7.2
Question 14.
54\(\frac{3}{11}\) = ____________
Answer:
First, write \(\frac{3}{11}\) as a decimal.
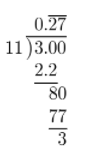
Then, add 54 to the result.
54 + \(0 . \overline{27}\) = \(54 . \overline{27}\)
= \(54 . \overline{27}\)
Question 15.
3\(\frac{1}{18}\) = _________
Answer:
First, write \(\frac{1}{18}\) as a decimal.
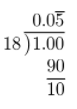
Then, add 3 to the result.
3 + \(0.0 \overline{5}\) = \(3.0 \overline{5}\)
= \(3.0 \overline{5}\)
Question 16.
Maggie bought 3\(\frac{2}{3}\) lb of apples to make some apple pies. What is the weight of the apples written as a decimal? (Example 2)
3\(\frac{2}{3}\) = ______________
Answer:
First, write \(\frac{2}{3}\) as a decimal.
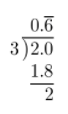
Then, add 3 to the result.
3 + \(0 . \overline{6}\) = \(3 . \overline{6}\)
Maggie bought \(3 . \overline{6}\) lb of apples.
Question 17.
Harry’s dog weighs 12\(\frac{7}{8}\) pounds. What is the weight of Harry’s dog written as a decimal? (Example 2)
12 \(\frac{7}{8}\) = _____________
Answer:
First, write \(\frac{7}{8}\) as a decimal.
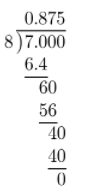
Then, add 12 to the result.
12 + 0.875 = 12.875
Harry’s dog weighs 12.875 pounds.
Essential Question Check-In
Question 18.
Tom is trying to write \(\frac{3}{47}\) as a decimal. He used long division and divided until he got the quotient 0.0638297872, at which point he stopped. Since the decimal doesn’t seem to terminate or repeat, he concluded that \(\frac{3}{47}\) is not rational. Do you agree or disagree? Why?
Answer:
Tom was wrong to conclude that \(\frac{3}{47}\) is not rational. First of all. \(\frac{3}{47}\) is a fraction. Thus, \(\frac{3}{47}\) is a rational number. After some time of long division, the patter would appear.
I disagree. \(\frac{3}{47}\) is a rational number.
Texas Go Math Grade 7 Lesson 1.1 Independent Practice Answer Key
Use the table for 19-23. Write each ratio in the form \(\frac{a}{b}\) and then as a decimal. Tell whether each decimal is a terminating or a repeating decimal.

Question 19.
basketball players to football players
Answer:
\(\frac{5}{11}\) is the ratio of basketball players to football players.
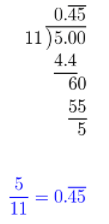
The equivalent decimal is a repeating decimal.
\(\frac{5}{11}\) = \(0 . \overline{45}\); repeating decimal
Question 20.
hockey players to lacrosse players
Answer:
\(\frac{6}{10}\) is the ratio of basketball players to football players.
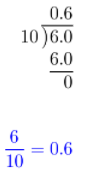
The equivalent decimal is a terminating decimal.
\(\frac{6}{10}\) = 0.6; terminating decimal.
Question 21.
polo players to football players
Answer:
\(\frac{4}{11}\) is the ratio of polo players to football players.

The equivalent decimal is a repeating decimal.
\(\frac{4}{11}\) = \(0 . \overline{36}\); repeating decimal.
Question 22.
lacrosse players to rugby players
Answer:
\(\frac{10}{15}\) is the ratio of basketball lacrosse players to football players.

The equivalent decimal is a repeating decimal.
\(\frac{10}{15}\) = \(0 . \overline{6}\); repeating decimal.
Question 23.
football players to soccer players
Answer:
\(\frac{11}{11}\) is the ratio of football players to soccer players.
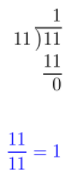
The equivalent decimal is a terminating decimal (.0).
\(\frac{11}{11}\) = 1; terminatimg decimal.
Question 24.
Look for a Pattern Beth said that the ratio of the number of players in any sport to the number of players on a lacrosse team must always be a terminating decimal. Do you agree or disagree? Why?
Answer:
I agree. The number of lacrosse players on a team is equal to 10. Since in any other sport the number of players on a team must be a whole number. Thus, by dividing any whole number by 10. you just “ move” the decimal point one spot to the left.
Example: Number of soccer players on a team is 11.
The ratio of soccer players on a team to lacrosse players on a team is \(\frac{11}{10}\)
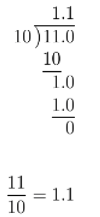
The ratio will always have a terminating decimal.
Question 25.
Yvonne bought 4\(\frac{7}{8}\) yards of material to make a dress.
a. What is 4\(\frac{7}{8}\) written as an improper fraction?
Answer:
4 × 8 + 7 = 39
4\(\frac{7}{8}\) = \(\frac{39}{8}\)
b. What is 4\(\frac{7}{8}\) written as a decimal?
Answer:
First, write \(\frac{7}{8}\) as a decimal.
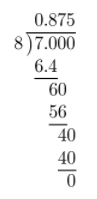
Then, add 4 to the result
4 + 0.875 = 4.875
c. Communicate Mathematical Ideas If Yvonne wanted to make 3 dresses that use 4\(\frac{7}{8}\) yd of fabric each, explain how she could use estimation to make sure she has enough fabric for all of them.
Answer:
Yvonne could multiply 4\(\frac{7}{8}\) by 3 and then buy some more yards (1 or 2) of fabric to ensure she would have enough to make 3 dresses.
Question 26.
Vocabulary A rational number can be written as the ratio of one _________ to another and can be represented by a repeating or ________ decimal.
Answer:
A rational number can be written as the ratio of one integer to another and can be represented by a repeating or a terminating decimal.
Question 27.
Problem Solving Marcus is 5\(\frac{7}{24}\) feet tall. Ben is 5\(\frac{5}{16}\) feet tall. Which of the two boys is taller? Justify your answer.
Answer:
Since both boys are 5 and something feet tall, we can just compare the fraction in the mixed numbers to find out which boy is taller.
Compare it by reducing to a common denominator or converting to a decimal number.
Since it is not so easy to convert those fractions to decimal numbers we will reduce to a common denominator.
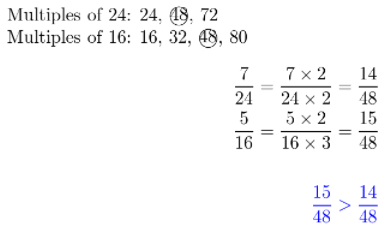
Ben is taller than Marcus.
Question 28.
Represent Real-World Problems If one store is selling \(\frac{3}{4}\) of a bushel of apples for $9, and another store is selling \(\frac{2}{3}\) of a bushel of apples for $9, which store has the better deal? Explain your answer.
Answer:
They both offer some amount of apples for the same price of $9.
The store which offers greater amount of tipples for the price of $9 has the better deal.
Convert fractions to decimal numbers.
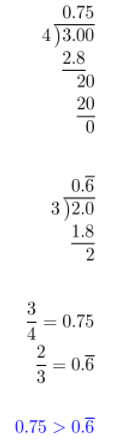
The first store has a better offer.
Question 29.
Analyze Relationships You are given a fraction in simplest form. The numerator is not zero. When you write the fraction as a decimal, it is a repeating decimal. Which numbers from 1 to 10 could be the denominator?
Answer:
The denominator could be a prime number (except 2 and 5) or a number that has a prime number in its factored form (again except 2 and 5).
These numbers from 1 to 10 are: 3, 6 = 2 × 3, 7, 9 = 3 × 3
Question 30.
Communicate Mathematical Ideas Julie got 21 of the 23 questions on her math test correct. She got 29 of the 32 questions on her science test correct. On which test did she get a higher score? Can you compare the fractions \(\frac{21}{23}\) and \(\frac{29}{32}\) by comparing 29 and 21 ? Explain. How can Julie compare her scores?.
Answer:
Divide the number of correct answers to the number of alt questions on both tests (round to 3 decimal digits).
Compare those decimaL numbers to see on which test she scored better
21 ÷ 23 = 0.913
29 ÷ 32 = 0.906
0.913 > 0.906
She got a higher score on the first test.
You can not compare those fractions by comparing 29 and 21 because the denominators are not equal. You could do that if they would be equal.
Question 31.
Look for a Pattern Look at the decimal 0.121122111222…. If the pattern continues, is this a repeating decimal? Explain.
Answer:
It is not a repeating decimal if the pattern continues
This is not a repeating pattern. This pattern is created by adding 1 and 2 after 1 and 2 respectively.
The pattern of a repeating decimal has to repeating without adding any other decimal in the pattern
Example:
0.567567567… = \(0 . \overline{567}\) Is a repeating decimal.
0.56556555655556… IS NOT a repeating decimal because the pattern has an additional 5 at every repetition.
This is not a repeating decimal if the pattern continues.