Refer to our Texas Go Math Grade 6 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 8 Module 9 Quiz Answer Key.
Texas Go Math Grade 6 Module 9 Quiz Answer Key
Texas Go Math Grade 6 Module 9 Ready to Go On? Answer Key
9.1 Understanding Percent
Shade the grid and write the equivalent percent for each fraction.
Question 1.
\(\frac{19}{50}\) ________________

Answer:
Given fraction = \(\frac{19}{50}\)
Multiply the given fraction with 100% to convert it to an equivalent percentage, therefore:
= \(\frac{19}{50}\) × 100%
Evaluate:
= 38%
Shade 38 of the 100 square shown, therefore:

\(\frac{19}{50}\) = 38%
Question 2.
\(\frac{13}{20}\) ________________

Answer:
Given fraction = \(\frac{13}{20}\)
Multiply the given fraction with 100% to convert it to an equivalent percentage, therefore:
= \(\frac{13}{20}\) × 100%
Evaluate:
= 65%
Shade 65 of the 100 square shown, therefore:
\(\frac{13}{20}\) = 65%
9.2 Percents, Fractions, and Decimals
Write each number in two equivalent forms.
Question 3.
\(\frac{3}{5}\) _____________
Answer:
Write an equivalent fraction with a denominator of 100
\(\frac{3}{5}=\frac{3 \times 20}{5 \times 20}=\frac{60}{100}\) (Multiply both the numerator and denominator by 20)
Write the decimal equivalent
\(\frac{60}{100}\) = 0.60
Write the percent equivalent
\(\frac{60}{100}\) = 0.60 = 60% (Move the decimal point 2 places to the right)
Final solution ⇒ \(\frac{3}{5}\) = 0.6 = 60%
Question 4.
62.5% ______________
Answer:

Question 5.
0.24 ____________
Answer:
Given number = 0.24
Convert the given number to an equivalent percentage by multiplying it with 100%. The percentage is evaluated by moving the decimal 2 places to the right from its current position, therefore:
= 0.24 × 100% = 24%
To convert it to an equivalent fraction replace the % sign with × \(\frac{1}{100}\) and simplify:
= 24 × \(\frac{1}{100}\)
Divide out the common factor to simplify:
= \(\frac{6}{25}\)
⇒ 0.24 = 24% = \(\frac{6}{25}\)
Question 6.
\(\frac{31}{50}\) ______________
Answer:
Write an equivalent fraction with a denominator of 100
\(\frac{31}{50}=\frac{31 \times 2}{50 \times 2}=\frac{62}{100}\) (Multiply both the numerator and denominator by 2)
Write the decimal equivalent
\(\frac{62}{100}\) = 0.62
Write the percent equivalent.
\(\frac{62}{100}\) = 0.62 = 62% (Move the decimal point 2 places to the right)
Final Solution ⇒ \(\frac{31}{50}\) = 0.62 = 62%
Question 7.
Selma spent \(\frac{7}{10}\) of her allowance on a new backpack. What percent of her allowance did she spend?
Answer:
Given Fraction = \(\frac{7}{10}\)
Multiply the given fraction with 100% to convert it to an equivalent percentage, therefore:
= \(\frac{7}{10}\) × 100%
Evaluate:
= 70%
Selma spent 70% of her allowance on a new backpack.
9.3 Solving Percent Problems
Complete each sentence.
Question 8.
12 is 30% of
Answer:
Multiply by a fraction to find 12 is 30% of?
Multiply
Percent = \(\frac{12}{30}\) × 100%
= \(\frac{1200}{30}\)
= 40
Final Solution = 40
12 is 30% of 40
Question 9.
45% of 20 is
Answer:
Multiply by a fraction to find 45 % of 20
Write the percent as a fraction.
45% of 20 = \(\frac{45}{100}\) of 20
Multiply
\(\frac{45}{100}\) of 20 = \(\frac{45}{100}\) × 20
= \(\frac{900}{100}\)
= 9
Final solution = 9
45% of 20 is 9 tiles
Question 10.
18 is _________ % of 30.
Answer:
Multiply by a fraction to find 18 is ?% of 30
Multiply
Percent = \(\frac{18}{30}\) × 100%
= \(\frac{1800}{30}\)
= 60%
Final Solution = 60%
18 is 60% of 30
Question 11.
56 is 80% of
Answer:
Multiply by a fraction to find 56 is 80% of?
Multiply
Percent = \(\frac{56}{80}\) × 100%
= \(\frac{5600}{80}\)
= 70%
Final Solution = 70
56 is 80% of 70
Question 12.
A pack of cinnamon-scented pencils sells for $4.00. What is the sales tax rate if the total cost of the pencils is $4.32?
Answer:
Data:
Portion = 4.32 – 4 = 0.32
Total = 4
Percent = x
Write equation of percentage: Portion
Percent = \(\frac{\text { Portion }}{\text { Total }}\) × 100%
Substitute values:
x = \(\frac{0.32}{4}\) × 100%
Evaluate:
x = 8
The sales tax rate was 8%
Essential Question
Question 13.
How can you solve problems involving percents?
Answer:
Percents represent a portion of any total on a scale of 100. The equation of percentage is Percent = \(\frac{\text { Portion }}{\text { Total }}\) × 100%. If 2 of the 3 variables shown are given, the 3rd can be evaluated using this equation, for any problem.
Texas Go Math Grade 6 Module 9 Mixed Review Texas Test Prep Answer Key
Selected Response
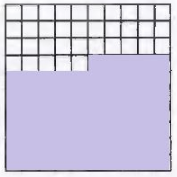
Question 1.
What percent does this shaded grid represent?

(A) 42%
(B) 48%
(C) 52%
(D) 58%
Answer:
(A) 42%
Explaination:
Since 42 of the 100 boxes are shaded, the percentage represented here is 42%.
Question 2.
Which expression is not equal to one fourth of 52?
(A) 0.25∙52
(B) 4% of 52
(C) 52 ÷ 4
(D) \(\frac{52}{4}\)
Answer:
(B) 4% of 52
Explaination:
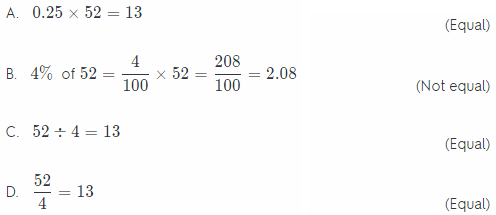
option B = This option is not equal
Question 3.
Approximately \(\frac{4}{5}\) of U.S. homeowners have a cell phone. What percent of homeowners do not have a cell phone?
(A) 20%
(B) 45%
(C) 55%
(D) 80%
Answer:
(A) 20%
Explaination:
Write an equivalent fraction with a denominator of 100
\(\frac{4}{5}=\frac{4 \times 20}{5 \times 20}=\frac{80}{100}\) (Multiply both the numerator and denominator by 20)
Write the decimal equivalent
\(\frac{80}{100}\) = 0.8
Write the percent equivalent
\(\frac{80}{100}\) = 0.8 = 80% (Move the decimal point 2 places to the right)
Therefore 100 – 80 = 20 % do not have a cell phone.
Question 4.
The ratio of rock music to total CDs that Ella owns is \(\frac{25}{40}\). Paolo has 50 rock music CDs. The ratio of rock music to total CDs in his collection is equivalent to the ratio of rock music to total CDs in Ella’s collection. How many CDs do they own?
(A) 65
(B) 80
(C) 120
(D) 130
Answer:
(C) 120
Explaination:
Note: This task is sloppily written. The sentence:
the ratio of rock music to total CDs that Ella owns is \(\frac{25}{40}\)
does not tell us how many CDs in total Ella has, and neither can we find out that (necessary) information from any other part of the task.
The ratio 25 : 40 is equivalent to, for example, 50 : 80, so the sentence the ratio of rock music to total CDs that Ella owns is \(\frac{50}{80}\)
would be equivalent to the one above, telling us that we can not determine the total number of Ella’s CDs from that information.
However, since the fraction \(\frac{25}{40}\) is not reduced all the way, it makes some sense to assume that Ella has 40 CDs in total.
Paul has x CDs in total 50 of which are rock, but also has the same ratio of rock music CDs to total CDs as Ella, so

Altogether, they own 40 + 80 = 120 CDs, so the correct answer is C)
Question 5.
Gabriel saves 40% of his monthly paycheck for college. He earned $270 last month. How much money did Gabriel save for college?
(A) $96
(B) $108
(C) $162
(D) $180
Answer:
(B) $108
Explaination:
Multiply by a fraction to find 40 % of 270
Write the percent as a fraction
Multiply
\(\frac{40}{100}\) of 270 = \(\frac{40}{100}\) × 270
= \(\frac{10800}{100}\) (this option is correct answer)
= 108
Gabriel saves 108 dollars.
Question 6.
Forty children from an after-school club went to the matinee. This is 25% of the children in the club. How many children are in the club?
(A) 10
(B) 160
(C) 200
(D) 900
Answer:
(B) 160
Explaination:
Multiply by a fraction to find 40 is 25% of x
Write the percent as a fraction
Multiply
x = \(\frac{40}{25}\) of 100 = \(\frac{40}{25}\) × 100
= \(\frac{4000}{25}\) (this option is correct answer)
x = 160
In the club are 160 children.
Question 7.
Dominic answered 43 of the 50 questions on his spelling test correctly. Which decimal represents the fraction of problems he answered incorrectly?
(A) 0.07
(B) 0.14
(C) 0.86
(D) 0.93
Answer:
(B) 0.14
Explaination:
The number of questions answered incorrectly are 50 – 43 = 7 Therefore, the fraction of incorrect answers is \(\frac{7}{50}\) = 0.14
Gridded Response
Question 8.
Jen bought some bagels. The ratio of the number of sesame bagels to the number of plain bagels that she bought is 1:3. Find the decimal equivalent of the percent of the bagels that are plain.
Answer:
The \(\frac{1}{3}\) of the bagels are with sesame, so
1 – \(\frac{1}{3}\) = \(\frac{3}{3}-\frac{1}{3}=\frac{2}{3}\)
are plain bagels.
\(\frac{2}{3}\) = 0.67 ≈ 67%