Refer to our Texas Go Math Grade 6 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 8 Module 7 Quiz Answer Key.
Texas Go Math Grade 6 Module 8 Quiz Answer Key
8.1 Comparing Additive and Multiplicative Relationships
Complete each table and describe the rule for the relationship.
Question 1.

Answer:
table – 1
This relationship is additive.
Swim time = Meat time + 45 minutes
Question 2.

Answer:
table – 2
The relationship is multiplicative.
Number of pens = Sets of pens ∙ 3
8.2 Ratios, Rates, Tables, and Graphs
Question 3.
Charlie runs laps around a track The table shows how long it takes him to run different numbers of laps. How long would it take Charlie to run 5 laps?
Answer:
Evaluate the rate here. Therefore, it takes \(\frac{10}{2}\) = 5 minutes per lap, so 5 laps will require 5 × 5 = 25 minutes.
Charlies takes 25 minutes to run 5 laps.
8.3 Solving Problems with Proportions
Question 4.
Emily is entering a bicycle race for charity. Her mother pledges $0.40 for every 0.25 mile she bikes. If Emily bikes 15 miles, how much will her mother donate? ___________________
Answer:
0.25 = 1 quarter of a mile and there are 1 quarters in 1 mile, so there are 1 × 4 = 60 quarters in 15 miles. Therefore. Emily’s mom will have to donate $0.40 × 60 = $ 24.
Result:
Emily’s mom will have to donate $ 24.
8.4 Converting Measurements
Convert each measurement.
Question 5.
18 meters = ______________ centimeters
Answer:
Find the conversion factor
Write 100 centimeters = 1 meter as a ratio: \(\frac{100 \text { centimeters }}{1 \text { meter }}\)
Multiply the given measurement by the conversion factor.
18 meters ∙ \(\frac{100 \text { centimeters }}{1 \text { meter }}\) = ? centimeters
18 meters ∙ \(\frac{100 \text { centimeters }}{1 \text { meter }}\) = 1800 centimeters [Cancel the common unit]
Final solution = 18 meters = 1800 centimeters
Question 6.
5 pounds = ____________ ounces
Answer:
Find the conversion factor
Write 16 ounces = 1 pound as a ratio: \(\frac{16 \text { ouncess }}{1 \text { pound }}\)
Multiply the given measurement by the conversion factor.
5 pounds ∙ \(\frac{16 \text { ouncess }}{1 \text { pound }}\) = ? ounces
5 pounds ∙ \(\frac{16 \text { ouncess }}{1 \text { pound }}\) = ? ounces [Cancel the common unit]
Final Solution = 5 pounds = 80 ounces
Question 7.
6 quarts = ____________ fluid ounces
Answer:
Find the conversion factor.
Write 32 fluid ounces = 1 quart as a ratio: \(\frac{32 \text { fluid ounces }}{1 \text { quart }}\)
Multiply the given measurement by the conversion factor
6 quarts \(\frac{32 \text { fluid ounces }}{1 \text { quart }}\) = ? fluid ounces
6 quarts \(\frac{32 \text { fluid ounces }}{1 \text { quart }}\) = 192 fluid ounces [Cancel the common unit]
Final Solution = 6 quarts = 192 fluid ounces
Question 8.
9 liters = _______________ milliliters.
Answer:
Find the conversion factor
Write 1000 milliliters = 1 liter as a ratio: \(\frac{1000 \text { militers }}{1 \text { liter }}\)
Multiply the given measurement by the conversion factor
9 liters ∙ \(\frac{1000 \text { militers }}{1 \text { liter }}\) = ? milliliters
9 liters ∙ \(\frac{1000 \text { militers }}{1 \text { liter }}\) = 9000 milliliters [Cancel the common unit]
Final Solution = 9 liters = 9000 milliliters
Essential Question
Question 9.
Write a real-world problem that could be solved using a proportion.
Answer:
A door is 7 feet tall. Evaluate its height in inches
1 feet is equal to 12 inches so 7 feet is equal to 7 × 12 = 84 inches. The door is 84 inches tall.
Texas Go Math Grade 6 Module 8 Mixed Review Texas Test Prep Answer Key
Selected Response
Question 1.
The table below shows the number of babies and adults at a nursery.
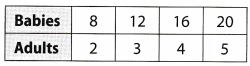
Which represents the number of babies?
(A) adults × 6
(B) adults × 6
(C) adults + 6
(D) adults + 6
Answer:
(B) adults × 6
Explaination:
The relationship is multiplicative.
Number of Babies = Number of adults ∙ 4
Question 2.
The graph represents the distance Manuel walks over several hours.
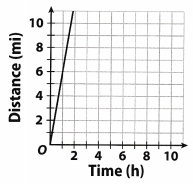
Which is an ordered pair on the line?
(A) (2.5, 14)
(B) (1,25, 5)
(C) (2.25, 12)
(D) (1.5, 9)
Answer:
(D) (1.5, 9)
Explaination:
plot all the given graph.
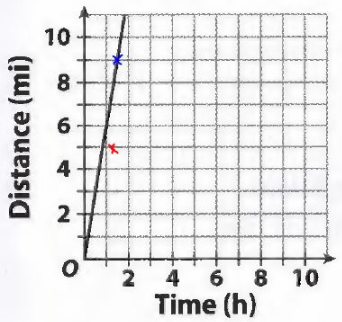
A and C can not be drawn as the y-axis ends on 11. It can be seen that only (1.5, 9) lies on the line shown.
Question 3.
On a map of the city, 1 inch represents 1.5 miles. What distance on the map would represent 12 miles?
(A) 6 inches
(B) 8 inches
(C) 12 inches
(D) 18 inches
Answer:
(C) 12 inches
Explaination:
\(\frac{\text { inches }}{\text { miles }}=\frac{1}{1.5}=\frac{x}{12}\)
112 is a common denominator:
\(\frac{1}{1.5} \cdot \frac{8}{8}=\frac{x}{12}\)
\(\frac{8}{12}=\frac{x}{12}\)
x = 12
Question 4.
The table below shows the number of petals and leaves for different numbers of flowers.
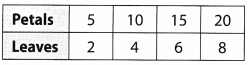
How many petals are present when there are 12 leaves?
(A) 25 petals
(B) 30 petals
(C) 35 petals
(D) 36 petals
Answer:
(B) 30 petals
Explaination:
It can be seen that there are \(\frac{5}{2}=\frac{10}{4}=\frac{15}{6}=\frac{20}{8}\) = 2.5 petals per leaf, therefore this implies that there must be 2.5 × 12 = 30 petals for 12 leaves.
Question 5.
A recipe calls for 3 cups of sugar and 9 cups of water. If the recipe is reduced, how many cups of water should be used with 2 cups of sugar?
(A) 3 cups
(B) 4 cups
(C) 6 cups
(D) 8 cups
Answer:
(C) 6 cups
Explaination:
The given ratio is 3 : 9 which simplifies to 1: 3, this implies that there are 3 cups of water for every 1 cup of sugar, therefore for 2 cups of sugar, 2 × 3 = 6 cups of water wilt be required.
Gridded Response
Question 6.
Janice bought 4 oranges for $3.40. What is the unit price?
Answer:
To find the rate, divide the numerator and denominator by 4.
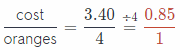
The cost per oranges is $ 0.85