Refer to our Texas Go Math Grade 6 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 6 Module 11 Quiz Answer Key.
Texas Go Math Grade 6 Module 11 Quiz Answer Key
Texas Go Math Grade 6 Module 11 Ready to Go On? Answer Key
11.1 Modeling Equivalent Expressions
Write each phrase as an algebraic expression.
Question 1.
p divided by 6 _________________
Answer:
Solution to this example is given below
p divided by 6. The operation is division. (Final solution)
The algebraic expression is \(\frac{p}{6}\)
\(\frac{p}{6}\)
Question 2.
65 less than j _________
Answer:
Solution to this example is given below
65 less than j. The operation is subtraction. (Final solution)
The algebraic expression is j – 65
j – 65
Question 3.
the sum of 185 and h _________
Answer:
The algebraic expression for the given statement: the sum of 185 and h is h + 185.
Question 4.
the product of 16 and g _____
Answer:
The algebraic expression for the given statement: the product of 16 and g is 16 × g = 16g,
16 × g = 16g
Question 5.
Let x represent the number of television show episodes that are taped in a season. Write an expression for the number of episodes taped in 4 seasons. _____________________
Answer:
The number of television show episodes that are taped in a season are x so in 4 seasons, there will be x × 4 = 4x episodes. There will be 4x episodes in 4 seasons.
11.2 Evaluating Expressions
Evaluate each expression for the given value of the variable.
Question 6.
8p; p = 9 _________________
Answer:
Solution to this example is given below
8p; p = 9
8(9) Substitute 9 for p
72 Multiply
When p = 9, 8p = 72
72 Final solution
Question 7.
11 + r; r = 7 _____
Answer:
Solution to this example is given below
11 + r; r = 7
11 + 7 Substitute 7 for r
18 Add
When r = 7, 11 + r = 18
18 Final solution
Question 8.
4(d + 7); d = -2 ___________
Answer:
Simplify the expression
= 4 (-2 + 7) substitute for the value of d
= 4(5) perform the operation inside the parenthesis then multiply
= 20
The value of the expression is 20.
Question 9.
\(\frac{-60}{m}\); m = 5 __________
Answer:
Solution to this example is given below
\(\frac{-60}{m}\); m = 5
\(\frac{-60}{5}\) Substitute 5 for m
-12 Divide
When m = 5, \(\frac{-60}{m}\) = -12
12 Final solution
Question 10.
To find the area of a triangle, you can use the expression b × h ÷ 2, where b is the base of the triangle and h is its height. What is the area of a triangle with a base of 6 and a height of 8? _______________________
Answer:
Solution to this example is given below
b × h ÷ 2; b = 6, h = 8
6 × 8 ÷ 2 Substitute 6 for b, and 8 for h
48 ÷ 2 Multiply
24 Divide
When b = 6, h = 8 b × h ÷ 2 = 24
Area of the triangle is 24 square units
24 Final solution
11.3 Generating Equivalent Expressions
Question 11.
Draw lines to match the expressions in List A with their equivalent expressions in List B.
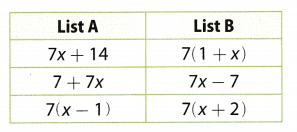
Answer:
a. of List B: Given expression:
7(1 + x)
Apply distributive property of multiplication to expand the parentheses:
= 7 + 7x
This is equal to b of List A.
c. of List B: Given expression:
7(x + 2)
Apply distributive property of multiplication to expand the parentheses:
= 7x + 14
This is equal to a of List A.
c. of List A: Given expression:
7(x – 1)
Apply distributive property of multiplication to expand the parentheses:
= 7x – 7
This is equal to b of List B
Essential Question
Question 12.
How can you determine if two algebraic expressions are equivalent?
Answer:
Problems involving equivalent expressions are solved using the rules of algebra. If 2 expressions are equivalent then they are identical in their simplified form.
Texas Go Math Grade 6 Module 11 Mixed Review Texas Test Prep Answer Key
Selected Response
Question 1.
Which expression represents the product of 83 and x?
(A) 83 + x
(B) 83 ÷ x
(C) 83x
(C) 83 – x
Answer:
(C) 83x
Explanation:
Product implies multiplication so the product of 83 and x is equal to 83 × x = 83x
Option C.
Question 2.
Which phrase describes the algebraic expression \(\frac{r}{9}\) ?
(A) the product of r and 9
(B) the quotient of r and 9
(C) 9 less than r
(D) r more than 9
Answer:
(B) the quotient of r and 9
Explanation:
\(\frac{r}{9}\) is a fraction which implies that r is divided by 9 or the quotient of r and 9
Option B
Question 3.
Rhonda was organizing photos in a photo album. She took 60 photos and divided them evenly among p pages. Which algebraic expression represents the number of photos on each page?
(A) P – 60
(B) 60 – p
(C) \(\frac{p}{60}\)
(D) \(\frac{60}{p}\)
Answer:
(D) \(\frac{60}{p}\)
Explanation:
A total of 60 photos are to be divided equal on p pages imply a problem of division where each page has \(\frac{60}{p}\) photos.
Option D
Question 4.
Using the algebraic expression 4n + 6, what is the greatest whole-number value of n that will give you a result less than 100?
(A) 22
(B) 23
(C) 24
(D) 25
Answer:
(B) 23
Explanation:
Given expression:
4n + 6
According to the given condition, the inequality becomes:
4n + 6 < 100
Solve for n:
4n < 100 – 6
Or
n < \(\frac{94}{4}\)
Simplify:
n < 23.5
Therefore, for n = 23, the value of the expression will be the greatest and less than 100.
Option B
Question 5.
Evaluate 7w – 14 for w = 9.
(A) 2
(B) 18
(C) 49
(D) 77
Answer:
(C) 49
Explanation:
Given expression: 7w – 14
Substitute the value of w:
7(9) – 14
Expand:
= 63 – 14
Evaluate:
= 49
Option (C)
Question 6.
Katie has read 32% of a book. If she has read 80 pages, how many more pages does Katie have left to read?
(A) 40
(B) 170
(C) 200
(D) 250
Answer:
(B) 170
Explanation:
Data:
Portion = 80
Total = x
Percent = 32
Write equation of percentage:
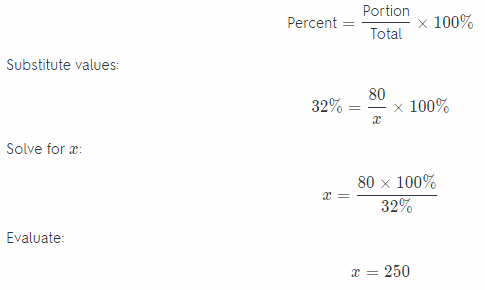
There are 250 pages in the book, 80 of them are read so 250 – 80 = 170 remain to be read.
Option B.
Question 7.
The expression 12(x + 4) represents the total cost of CDs Mel bought in April and May at $12 each. Which property is applied to write the equivalent expression 12x + 48?
(A) Associative Property of Addition
(B) Associative Property of Multiplication
(C) Commutative Property of Multiplication
(D) Distributive Property
Answer:
(D) Distributive Property
Explanation:
The operation in the expression is Multiplication
You can use the Distributive Property of Multiplication to write an equivalent expression: 12(x + 4) = 12x + 48 (This option is correct answer)
D
Gridded Response
Question 8.
When traveling in Europe, Bailey converts the temperature given in degrees Celsius to a Fahrenheit temperature by using the expression 9x ÷ 5 + 32, where x is the Celsius temperature. Find the temperature in degrees Fahrenheit when it is 15 °C.
Answer:
Determine the temperature in degrees Fahrenheit
= 9(15) ÷ 5 + 32 substitute for the value of x then multiply
= 135 ÷ 5 + 32 divide 135 by 5
= 27 + 32 add the numbers
= 59 temperature in degrees Fahrenheit
The answer in the grid must be 59.00.