Refer to our Texas Go Math Grade 6 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 6 Lesson 9.3 Answer Key Solving Percent Problems.
Texas Go Math Grade 6 Lesson 9.3 Answer Key Solving Percent Problems
Reflect
Question 1.
Justify Reasoning How did you determine the labels along the bottom of the bar model in Step D?
Answer:
Study the interval difference between 2 successive labels in the bottom label. Here it is 80 – 40 = 40 – 0 = 40.
This suggests that each unit represents 40 units so the next label after the 80 label is therefore 80 + 40 = 120 and so on.
Question 2.
Communicate Mathematical Ideas How can you use the bar model to find the number of left-handed gloves?
Answer:
Here 10% of gloves imply 40 gloves, so 30% would imply 40 × 3 = 120 gloves. This means that there are 120 left-handed gloves in the shipment.
Question 3.
Analyze Relationships In B, the percent is 35%. What is the part and what is the whole?
Answer:
The expression says: 35% of 60 so here 60 is the whole and 35% of 60 = \(\frac{35}{100}\) × 60 = 21 is the portion of it.
60 is whole and 21 is 35% of 60.
Question 4.
Communicate Mathematical Ideas Explain how to use proportional reasoning to find 35% of 600.
Answer:
Multiply by a fraction to find 35 % of 600
Write the percent as a fraction.
35% of 600 = \(\frac{35}{100}\) of 600
Multiply
\(\frac{35}{100}\) of 600 = \(\frac{35}{100}\) × 600
= \(\frac{21000}{100}\)
= 210
Final solution = 210
35% of 600 is 210
Your Turn
Find the percent of each number.
Question 5.
38% of 50 _____________
Answer:
Multiply by a fraction to find 38 % of 50
Write the percent as a fraction.
38% of 50 = \(\frac{38}{100}\) of 50
Multiply
\(\frac{38}{100}\) of 50 = \(\frac{38}{100}\) × 50
= \(\frac{1900}{100}\)
= 19
Final solution = 19
38% of 50 is 19
Question 6.
27% of 300 ____________
Answer:
Multiply by a fraction to find 27 % of 300
Write the percent as a fraction.
27% of 300 = \(\frac{27}{100}\) of 300
Multiply
\(\frac{27}{100}\) of 300 = \(\frac{27}{100}\) × 300
= \(\frac{8100}{100}\)
= 81
Final solution = 81
27% of 300 is 81
Question 7.
60% of 75 ____________
Answer:
Multiply by a fraction to find 60 % of 72
Write the percent as a fraction.
60% of 75 = \(\frac{60}{100}\) of 75
Multiply
\(\frac{60}{100}\) of 75 = \(\frac{60}{100}\) × 75
= \(\frac{4500}{100}\)
= 45
Final solution = 45
60% of 75 is 45
Reflect
Question 8.
Communicate Mathematical Ideas Write 57% as a ratio. Which number in the ratio represents the part and which number represents the whole? Explain.
Answer:
57% when written as an equivalent fraction is \(\frac{57}{100}\) or 57 : 100 as a rati0. Here 100 is the whole and 57 is the portion.
Your Turn
Question 9.
Out of the 25 students in Mrs. Green’s class, 19 have a pet. What percent of the students in Mrs. Green’s class have a pet? ______________
Answer:
There are a total of 25 students in the class out which 19 have pets, so the fraction of students who have pets is \(\frac{19}{25}\).
Multiply this fraction with 100% to convert to an equivalent percentage, therefore: \(\frac{19}{25}\) × 100% = 76%.
76% of the students in Mrs. Green’s class have a pet.
Reflect
Question 10.
Multiple Representations Sixteen students in the school band play clarinet. Clarinet players make up 20% of the band. Use a bar model to find the number of students ¡n the school band.

Answer:
20% of the number of students is 16.
Divide this number by 2 to find the 10%
10% is equal to 8.
Your Turn
Question 11.
6 is 30% of __________.
Answer:
let the total number here be x, then the equation of its portion is therefore:
30% of x = 6
Convert the given expression to an algebraic expression by replacing the percentage sign with × \(\frac{1}{100}\) and the word of with ×, so the expression becomes:
30 × \(\frac{1}{100}\) × x = 6
Solve for x:
x = \(\frac{6}{0.3}\)
Evaluate:
x = 20
6 is 30% of 20
Question 12.
15% of ___________ is 75.
Answer:
let the total number here be x, then the equation of its portion is therefore:
15% of x = 75
Convert the given expression to an algebraic expression by replacing the percentage sign with × \(\frac{1}{100}\) and the word of with ×, so the expression becomes:
15 × \(\frac{1}{100}\) × x = 75
Solve for x:
x = \(\frac{75}{0.15}\)
Evaluate:
x = 500
75 is 15% of 500.
Texas Go Math Grade 6 lesson 9.3 Guided Practice Answer Key
Question 1.
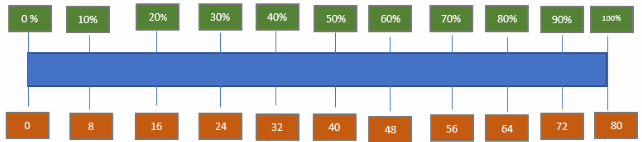
A store has 300 televisions on order, and 80% are high definition.
a. Use the bar model and complete the bottom of the bar.

Answer:
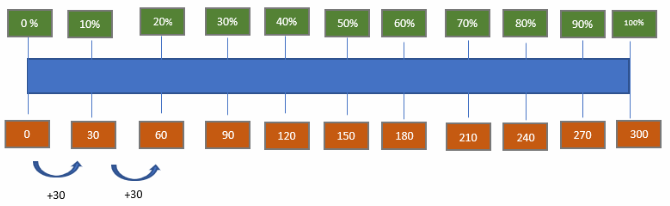
b. Complete the diagram to model this situation.
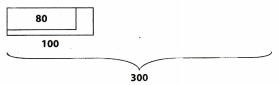
Answer:
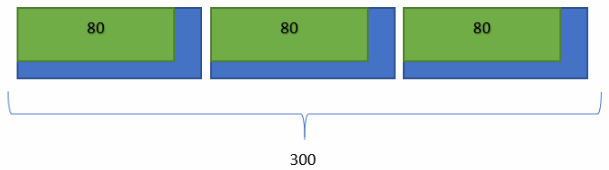
C. How many televisions on the order are high definition?
Answer:
We can see that 80% of 300 is equal to 240
Question 2.
Use proportional reasoning to find 65% of 200.
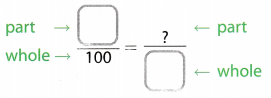
Answer:
Multiply by a fraction to find 65 % of 200
Write the percent as a fraction
65% of 200 = \(\frac{65}{100}\) of 200
Multiply
\(\frac{65}{100}\) of 200 = \(\frac{65}{100}\) × 200
= \(\frac{13000}{100}\)
= 130
Final solution = 130
65% of 200 is 130
Question 3.
Use multiplication to find 5% of 180
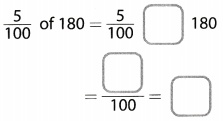
5% of 180 is ___________ .
Answer:
Multiply by a fraction to find 5 % of 180
Write the percent as a fraction
5% of 180 = \(\frac{5}{100}\) of 180
Multiply
\(\frac{5}{100}\) of 180 = \(\frac{5}{100}\) × 180
= \(\frac{900}{100}\)
= 9
Final solution = 9
5% of 180 is 9
Question 4.
Ala na spent $21 of her $300 paycheck on a gift. What percent of her paycheck was spent on the gift? (Example 2)
Alana spent _____ of her paycheck on the gift.
Answer:
\(\frac{\text { gift }}{\text { paycheck }}=\frac{21}{300}=\frac{x}{100}\)
100 is a common denominator:
\(\frac{21}{300} \div \frac{3}{3}=\frac{x}{100}\)
\(\frac{7}{100}=\frac{x}{100}\)
⇒ x = 7 ⇒ 7%
Question 5.
At Pizza Pi, 9% of the pizzas made last week had extra cheese. If 27 pizzas had extra cheese, how many pizzas in all were made last week? ExampIe 3)
There were ______ pizzas made last week.
Answer:
\(\frac{\text { extra cheese }}{\text { pizza }}=\frac{9}{100}=\frac{27}{x}\)
127 is a common numerator:
\(\frac{9}{100} \cdot \frac{3}{3}=\frac{27}{x}\)
\(\frac{27}{300}=\frac{27}{x}\)
⇒ x = 300
Essential Question Check-In
Question 6.
How can you use proportional reasoning to solve problems involving percent?
Answer:
Proportional reasoning to solve problems involving percent by converting the given percentage to an equivalent fraction and equating it with the given fraction of \(\frac{\text { Portion }}{\text { Whole }}\)
Find the percent of each number.
Question 7.
64% of 75 tiles
Answer:
Multiply by a fraction to find 64 % of 75
Write the percent as a fraction
64% of 75 = \(\frac{64}{100}\) of 75
Multiply
\(\frac{64}{100}\) of 75 = \(\frac{64}{100}\) × 75
= \(\frac{4800}{100}\)
= 48
Final solution = 48
64% of 75 is 48 tiles
Question 8.
20% of 70 plants
Answer:
Multiply by a fraction to find 20 % of 70 plants
Write the percent as a fraction
20% of 70 = \(\frac{20}{100}\) of 70
Multiply
\(\frac{20}{100}\) of 70 = \(\frac{20}{100}\) × 70
= \(\frac{1400}{100}\)
= 14
Final solution = 14
20% of 70 is 14 plants
Question 9.
32% of 25 pages
Answer:
Multiply by a fraction to find 32 % of 25 pages
Write the percent as a fraction
32% of 25 = \(\frac{32}{100}\) of 25
Multiply
\(\frac{32}{100}\) of 25 = \(\frac{32}{100}\) × 75
= \(\frac{800}{100}\)
= 8
Final solution = 8
32% of 25 is 8 pages.
Question 10.
85% of 40 e-mails
Answer:
Multiply by a fraction to find 85% of 40 e-mails
Write the percent as a fraction
85% of 40 = \(\frac{85}{100}\) of 40
Multiply
\(\frac{85}{100}\) of 40 = \(\frac{85}{100}\) × 40
= \(\frac{3400}{100}\)
= 34
Final solution = 34
85% of 40 is 34 e-mails
Question 11.
72% of 350 friends
Answer:
Multiply by a fraction to find 72% of 350 friends
Write the percent as a fraction
72% of 350 = \(\frac{72}{100}\) of 350
Multiply
\(\frac{72}{100}\) of 350 = \(\frac{72}{100}\) × 350
= \(\frac{25200}{100}\)
= 252
Final solution = 252
72% of 350 is 252 friends
Question 12.
5% of 220 files
Answer:
Multiply by a fraction to find 5% of 220 friends
Write the percent as a fraction
5% of 220 = \(\frac{5}{100}\) of 220
Multiply
\(\frac{5}{100}\) of 220 = \(\frac{5}{100}\) × 220
= \(\frac{1100}{11}\)
= 11
Final solution = 11
5% of 350 is 220 is 11 files.
Complete each sentence.
Question 13.
4 students is ______ % of 20 students.
Answer:
Multiply by a fraction to find 4 students is ? of 20 students
Multiply
Percent = \(\frac{4}{20}\) × 100%
= \(\frac{400}{20}\)
= 20%
Final Solution = 20%
4 students is 20% of 20 students
Question 14.
2 doctors is ______ % of 25 doctors.
Answer:
Multiply by a fraction to find 2 doctors is ? of 25 doctors
Multiply
Percent = \(\frac{2}{25}\) × 100%
= \(\frac{200}{25}\)
= 8%
Final Solution = 8%
2 doctors is 8% of 25 doctors.
Question 15.
_______ % of 50 shirts is 35 shirts.
Answer:
Multiply by a fraction to find ? % of 50 shirts is 35 shirts
Multiply
Percent = \(\frac{35}{50}\) × 100%
= \(\frac{3500}{50}\)
= 70%
Final Solution = 70%
70% of 50 shirts is 35 shirts
Question 16.
______ % of 200 miles is 150 miles.
Answer:
Multiply by a fraction to find ? % of 200 miles is 150 miles
Multiply
Percent = \(\frac{150}{200}\) × 100%
= \(\frac{15000}{200}\)
= 75%
Final Solution = 75%
75% of 200 miles is 150 miles
Question 17.
4% of ______ days is 56 days.
Answer:
Multiply by a fraction to find 4 % of ? days is 56 days
Multiply
Percent = \(\frac{56}{4}\) × 100%
= \(\frac{56000}{4}\)
= 1400
Final Solution = 1400
4% of 1400 days is 56 days.
Question 18.
60 minutes is 20% of ______ minutes.
Answer:
Multiply by a fraction to find 60 minutes is 20% of ? minutes.
Multiply
Percent = \(\frac{60}{20}\) × 100%
= \(\frac{6000}{20}\)
= 300
Final Solution = 300
60 minutes is 20% of 300 minutes.
Question 19.
80% of ______ games is 32 games.
Answer:
Multiply by a fraction to find 80% of ? games is 32 games
Multiply
Percent = \(\frac{32}{80}\) × 100%
= \(\frac{3200}{80}\)
= 40
Final Solution = 40
80% of 40 games is 32 games
Question 20.
360 kilometers is 24% of ______ kilometers.
Answer:
Multiply by a fraction to find 360 kilometers is 24% of ? kilometers.
Multiply
Percent = \(\frac{360}{24}\) × 100%
= \(\frac{36000}{24}\)
= 1500
Final Solution = 1500
360 kilometers is 24% of 1500 kilometers
Question 21.
75% of ______ peaches is 15 peaches.
Answer:
Multiply by a fraction to find 75% of ? peaches is 15 peaches.
Multiply
Percent = \(\frac{15}{75}\) × 100%
= \(\frac{1500}{75}\)
= 20
Final Solution = 2
75% of 20 peaches is 15 peaches
Question 22.
9 stores is 3% of ______ stores.
Answer:
Multiply by a fraction to find 9 stores is 3 % of ? stores
Multiply
Percent = \(\frac{9}{3}\) × 100%
= \(\frac{900}{3}\)
= 300
Final Solution = 300
9 stores is 3% of 300 stores
Question 23.
At a shelter, 15% of the dogs are puppies.
There are 60 dogs at the shelter.
How many are puppies? _______ puppies
Answer:
Multiply by a fraction to find 15 % of 60
Write the percent as a fraction.
15% of 60 = \(\frac{15}{100}\) of 60
Multiply
\(\frac{15}{100}\) of 60 = \(\frac{15}{100}\) × 60
= \(\frac{900}{100}\)
= 9
Final solution = 9
15% of 60 is 9 puppies
Question 24.
Carl has 200 songs on his MP3 player. Of these songs, 24 are country songs. What percent of Carl’s songs are country songs? ______
Answer:
Multiply by a fraction to find ? % of 200 songs is 24 country songs
Multiply
Percent = \(\frac{24}{100}\) × 100%
= \(\frac{2400}{200}\)
= 12%
Final Solution = 12%
12% of 200 songs is 24 country songs
Question 25.
Consumer Math The sales tax in the town where Amanda lives is 7%. Amanda paid $35 in sales tax on a new stereo. What was the price of the stereo? ______
Answer:
Multiply by a fraction to find 7 % is 35 of × dollars
Write the percent as a fraction.
7% = \(\frac{35}{x}\) × 100
Multiply
x = \(\frac{35}{7}\) × 100%
= \(\frac{3500}{100}\)
= 500
Final Solution = 500
7 % is 35 dollars of 500 dollars
The price of the stereo was 500 dollars
Question 26.
Financial literacy Ashton is saving money to buy a new bike. He needs $120 but has only saved 60% so far. How much more money does Ashton need to buy the scooter?
Answer:
Portion = x
Total = 120
Percent = 60
Write equation of percentage:
Percent = \(\frac{\text { Portion }}{\text { Total }}\) × 100%
Substitute values:
60% = \(\frac{x}{120}\) × 100%
Solve for x:
x = \(\frac{120 \times 60 \%}{100 \%}\)
Evaluate:
x = 72
He has saved $72 so he needs 120 – 72 = $ 48 more.
Ashton needs $48 more to buy the scooter.
Question 27.
Consumer Math Monica paid sales tax of $1.50 when she bought a new bike helmet. If the sales tax rate was 5%, how much did the store charge for the helmet before tax? ______
Answer:
Portion = 1.5
Total = x
Percent = 5
Write equation of percentage:
Percent = \(\frac{\text { Portion }}{\text { Total }}\) × 100%
Substitute values:
5% = \(\frac{1.5}{x}\) × 100%
Solve for x:
x = \(\frac{1.5 \times 100 \%}{5 \%}\)
Evaluate:
x = 30
The store charged $30 for the helmet before tax.
Ashton needs $48 more to buy the scooter.
Question 28.
Use the circle graph to determine how many hours per day Becky spends on each activity.

School: ______ hours
Eating: ______ hours
Sleep: ______ hours
Homework: ______ hours
Free time: ______ hours
Answer:
There are a total of 24 hours in day, so evaluate the time in hours spent ¡n each activity by converting the given percentage to an equivalent fraction by removing the percentage sign and dividing it by 100 and multiplying it with 24, therefore:
Time spent in eating = \(\frac{10}{100}\) × 24 = 2.4
Time spent in free time = \(\frac{15}{100}\) × 24 = 3.6
Time spent in homework = \(\frac{10}{100}\) × 24 = 2.4
Time spent in school = \(\frac{25}{100}\) × 24 = 6
time spent in sleeping = \( \frac{40}{100}\) × 24 = 9.6
H.O.T. Focus On Higher Order Thinking
Question 29.
Multistep Marc ordered a rug. He gave a deposit of 30% of the cost and will pay the rest when the rug is delivered. If the deposit was $75, how much more does Marc owe? Explain how you found your answer.
Answer:
Portion = 75
Total = x
Percent = 30
Write equation of percentage:
Percent = \(\frac{\text { Portion }}{\text { Total }}\) × 100%
Substitute values:
30% = \(\frac{75}{x}\) × 100%
Solve for x:
x = \(\frac{75 \times 100 \%}{30 \%}\)
Evaluate:
x = 250
The total cost of the rug was $250. Since, $75 is paid, only 250 – 75 = $ 175 remains to be paid.
$175 remains to be paid.
Question 30.
Earth Science Your weight on different planets is affected by gravity. An object that weighs 150 pounds on Earth weighs only 56.55 pounds on Mars. The same object weighs only 24.9 pounds on the Moon.
a. What percent of an object’s Earth weight is its weight on Mars and on the Moon?
Answer:
\(\frac{\text { Mars }}{\text { Earth }}=\frac{56.55}{150}=\frac{x}{100}\)
100 is a common denominator:
\(\frac{56.55}{150} \div \frac{1.5}{1.5}=\frac{x}{100}\)
\(\frac{37.7}{100}=\frac{x}{100}\)
⇒ x = 37.7 ⇒ 37.7%
\(\frac{\text { Moon }}{\text { Earth }}=\frac{24.9}{150}=\frac{x}{100}\)
100 is a common denominator:
\(\frac{24.9}{150} \div \frac{1.5}{1.5}=\frac{x}{100}\)
\(\frac{16.6}{100}=\frac{x}{100}\)
⇒ x = 16.6 ⇒ 16.6%
b. Suppose x represents an object’s weight on Earth. Write two expressions: one that you can use to find the object’s weight on Mars and another that you can use to write the object’s weight on the Moon.
Answer:

c. The space suit Neil Armstrong wore when he stepped on the Moon for the first time weighed about 180 pounds on Earth. How much did it weigh on the Moon?
Answer:
Moon = \(\frac{37.7}{100}\) ∙ Earth
Moon = \(\frac{37.7}{100}\) ∙ 180 = 67.86
67.86 pounds.
d. What If? If you could travel to Jupiter, your weight would be 236.4% of your Earth weight. How much would Neil Armstrong’s space suit weigh on Jupiter?
Answer:
Jupiter = \(\frac{236.4}{100}\) ∙ Earth = \(\frac{236.4}{100}\) ∙ 180 = 425.52
425.52 pounds
Question 31.
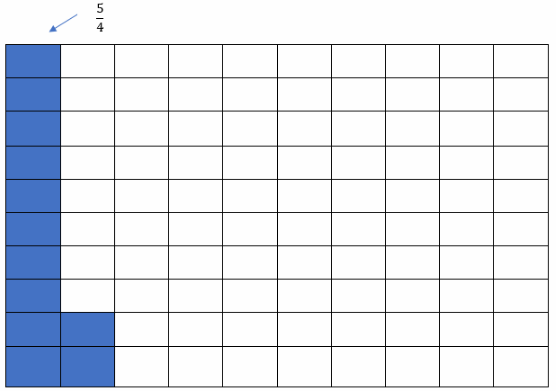
Explain the Error Fifteen students in the band play clarinet. These 15 students make up 12% of the band. Your friend used the proportion \(\frac{12}{100}=\frac{?}{15}\) to find the number of students in the band. Explain why your friend is incorrect and use the grid to find the correct answer.

Answer:
Friends used the wrong proportion The correct proportion would be:
\(\frac{12}{100}=\frac{15}{?}\)
because 15 students make up 12% of the whole group.
12% represents 15 students.
100 squares represents 100%.
12 squares represents 12%.
Since \(\frac{15}{12}\) = \(\frac{5}{4}\) ⇒ 1 square represents \(\frac{5}{4}\) student.
100 ∙ \(\frac{5}{4}\) = 125
so 100 squares represent 125 students.