Refer to our Texas Go Math Grade 6 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 6 Lesson 7.1 Answer Key Ratios.
Texas Go Math Grade 6 Lesson 7.1 Answer Key Ratios
Texas Go Math Grade 6 Lesson 7.1 Explore Activity Answer Key
Representing Ratios with Models
A ratio is a multiplicative comparison of two quantities expressed with the same units. The figure shows a ratio of 4 blue squares to 1 red square, or 4 to 1.

A bracelet has 3 star-shaped beads fer every 1 moon-shaped bead.

(A) Write the ratio of star beads to moon beads. ______________
(B) If the bracelet has 2 moon beads, how many star beads does it have? _______________
(C) If the bracelet has 9 star beads, how many moon beads does it have? How do you know? _______________
Reflect
Question 1.
Make a Prediction Write a rule that you can use to find the number of star beads when you know the number of moon beads.
Answer:
There are 4 units on the bracelet. 3 of them are star-shaped, and one is moon-shaped
The ratio of the star to moon beads is:
\(\frac{\text { star }}{\text { moon }}\) = \(\frac{3}{1}\)
That means, there are 3 times more stars beads than moon beads.
Question 2.
Make a Prediction Write a rule that you can use to find the number of moon beads when you know the number of star beads.
Answer:
There are 4 units on the bracelet. 3 of them are star-shaped, and one is moon-shaped.
The ratio of the moon to star beads is:
\(\frac{\text { moon }}{\text { star }}\) = \(\frac{1}{3}\)
That means, there are 3 times less moons beads than star beads.
Question 3.
Analyze Relationships Describe the relationship between the drama videos and the science fiction videos.
Answer:
There are 3 Drama videos and 1 Science fiction video, so it can be said that there are 3 times as many Drama videos as Science fiction videos.
Question 4.
Analyze Relationships The ratio of floor seats to balcony seats in a theater is 20:1. Does this theater have more floor seats or more balcony seats? How do you know?
Answer:
\(\frac{\text { floor }}{\text { balcony }}\) = \(\frac{20}{1}\)
That means, for every 20 floor seats
there is one balcony seat.
There are more floor seats.
Your Turn
Write each ratio ¡n three different ways.
Question 5.
bagel chips to peanuts ______________
Answer:
Write the ratio of bagel chips to peanuts in three different ways
part to part:
3 ÷ 1
\(\frac{3}{1}\)
3 cups of bagel chips to 1 cup of peanuts
Question 6.
total party mix to pretzels ____________
Answer:
Write the ratio of total party mix to pretzels in three different ways
part to part:
8 ÷ 3
\(\frac{8}{3}\)
8 total party mix to 3 cups of pretzels
Question 7.
cheese crackers to peanuts ___________
Answer:
Write the ratio of chees crackers to peanuts in three different ways
part to part
1 ÷ 1
\(\frac{1}{1}\)
1 cup cheese crackers to 1 cup of peanuts
The number of dogs compared to the number of cats owned by the residents of an apartment complex is represented by the model shown.

Find three ratios equivalent to the given ratio.
Question 8.
\(\frac{8}{10}\) ______________
Answer:
Given
\(\frac{8}{10}\)
Multiply both the numerator and the denominator of the given ratio with the same number to obtain an equivalent ratio, therefore:
\(\frac{8}{10}=\frac{8 \times 2}{10 \times 2}=\frac{16}{20}\)
And:
\(\frac{8}{10}=\frac{8 \times 3}{10 \times 3}=\frac{24}{30}\)
And:
\(\frac{8}{10}=\frac{8 \times 4}{10 \times 4}=\frac{32}{40}\)
Question 9.
\(\frac{5}{2}\) ______________
Answer:
Given
\(\frac{5}{2}\)
Multiply both the numerator and the denominator of the given ratio with the same number to obtain an equivalent ratio, therefore:
\(\frac{5}{2}=\frac{5 \times 2}{2 \times 2}=\frac{10}{4}\)
And:
\(\frac{5}{2}=\frac{5 \times 3}{2 \times 3}=\frac{15}{6}\)
And:
\(\frac{5}{2}=\frac{5 \times 4}{2 \times 4}=\frac{20}{8}\)
Texas Go Math Grade 6 Lesson 7.1 Guided Practice Answer Key
Question 1.
Write a ratio that compares the number of dogs to the number of cats. _______________
Answer:
Write the ratio of the number of dogs to the number of cats in two different ways
part to part
1 ÷ 5, \(\frac{1}{5}\)
Question 2.
If there are 15 cats in the apartment complex, how many dogs are there?
15 ÷ _________ = _________ dogs
Answer:
For the given condition, the proportion becomes:
\(\frac{1}{5}\) = \(\frac{x}{15}\)
Solve for x:
x = \(\frac{1}{5}\) × 15
Evaluate:
x = 3
3 dogs.
Question 3.
How many cats are there if there are 5 dogs in the apartment complex?
5 × _________ = ________ cats
Answer:
For the given condition, the proportion becomes:
\(\frac{1}{5}\) = \(\frac{5}{x}\)
Solve for x:
x = 5 × 5
Evaluate:
x = 25
25 cats.
The contents of Dana’s box of muffins is shown. Write each ratio in three different ways.

Question 4.
Banana nut muffins to chocolate chip muffins ______________
Answer:
The ratio of banana nuts to chocolate chips:
\(=\frac{\text { banana nut }}{\text { chocolate chip }}\) = \(\frac{2}{6}\)
The ratio can also be written as
2 to 6
or
2 : 6
or
\(\frac{2}{6}\)
Question 5.
Bran muffins to total muffins ____________________
Answer:
There are
6 + 3 + 2 + 1 = 12 muffins
The ratio of bran to total number of muffins:
\(\frac{\text { bran }}{\text { total }}\) = \(\frac{3}{12}\)
This ratio can also be written as
3 to 12
or
3 : 12
or
\(\frac{3}{12}\)
Write three equivalent ratios for the given ratio.
Question 6.
\(\frac{10}{12}\) ___________
Answer:
Multiply the numerator and denominator by the same number:
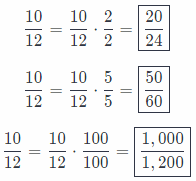
\(\frac{20}{24}\), \(\frac{50}{60}\), \(\frac{1,000}{1,200}\)
Question 7.
\(\frac{14}{2}\) ___________
Answer:
Multiply the numerator and denominator by the same number:
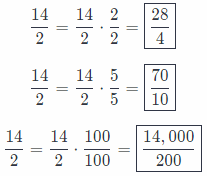
\(\frac{28}{4}\), \(\frac{70}{10}\), \(\frac{14,000}{200}\)
Question 8.
\(\frac{4}{7}\) ___________
Answer:
Multiply the numerator and denominator by the same number:

\(\frac{8}{14}\), \(\frac{20}{35}\), \(\frac{400}{700}\)
Essential Question Check-In
Question 9.
Use an example to describe the multiplicative relationship between two equivalent ratios.
Answer:
Example:
Given ratio:
\(\frac{4}{7}\)
Multiply both the numerator and the denominator of the given ratio with the same number to obtain an equivalent ratio, therefore:
\(\frac{4}{7}=\frac{4 \times 2}{7 \times 2}=\frac{8}{14}\)
And:
\(\)
And:
\(\frac{4}{7}=\frac{4 \times 4}{7 \times 4}=\frac{16}{28}\)
It can be seen that all. equivalent ratios when simplified, reduce to the same fraction in their simplest form. This is the multiplicative relationship between equivalent ratios.
Equivalent ratios have the same reduced from.
Question 10.
Draw a model to represent the ratio 1 to 3. Describe how to use the model to find an equivalent ratio.
Answer:
Padme and Anakin have 4 childrens: Leia (girl), Luke, Han and Obi (boys). So the ratio of girls to boys is:
\(\frac{\text { girls }}{\text { boys }}=\frac{1}{3}\)
To find an equivalent ratio, multiply numerator and denominator by the same number:
\(\frac{1}{3}=\frac{1}{3} \cdot \frac{2}{2}=\frac{2}{6}\)
Question 11.
The ratio of boys to girls on the bus is \(\frac{20}{15}\) Find three ratios equivalent to the described ratio.
Answer:
Multiply or divide the numerator and denominator by the same number:
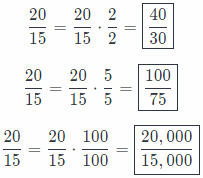
\(\frac{40}{30}\), \(\frac{100}{75}\), \(\frac{20,000}{15,000}\)
Question 12.
In each bouquet of flowers, there are 4 roses and 6 white carnations. Complete the table to find how many roses and carnations there are in 4 bouquets of flowers.

Answer:
| Number of bouquets | Roses | Carnations |
| 1 | 4 | 6 |
| 2 | 2 × 4 = 8 | 2 × 6 = 12 |
| 3 | 3 × 4 = 12 | 3 × 6 = 18 |
| 4 | 4 × 4 = 16 | 4 × 6 = 24 |
Question 13.
Ed is using the recipe shown to make fruit salad. He wants to use 30 diced strawberries in his fruit salad. How many bananas, apples, and pears should Ed use in his fruit salad?

Answer:
It can be seen that if he is using 30 diced strawberries, then he is making = 3 times the amount of salad given in the recipe, so multiply the quantity of each ingredient with 3 to evaluate the amount of ingredients required, therefore: 4 × 3 = 12 diced bananas are required, 3 × 3 = 9 diced apples are required and 6 × 3 = 18 diced pears are required.
124 diced bananas, 9 diced apples, 18 diced pears
Question 14.
A collector has 120 movie posters and 100 band posters. She wants to sell 24 movie posters but still have her poster collection maintain the same ratio of 120:100. If she sells 24 movie posters, how many band posters should she sell? Explain.
Answer:
The ratio to be maintained is 120 : 100 = \(\frac{120}{100}\). After selling 24 of the movie posters, she has sold, \(\frac{24}{120}\) × 100 = 20% of them, so she must sell 20% of the other posters too, that is 100 × 20% = 20. She must sell 20 band posters.
Question 15.
Bob needs to mix 2 cups of liquid lemonade concentrate with 3.5 cups of water to make lemonade. Bob has 6 cups of lemonade concentrate. How much lemonade can he make?
Answer:
The ratio of lemonade concentrate to water is:
\(\frac{\text { lemonade }}{\text { water }}=\frac{2}{3.5}\)
Multiply numerator and denominator by 3 to find the amount of the water he needs to use:
\(\frac{2}{3.5} \cdot \frac{3}{3}=\frac{6}{10.5}\)
He will mix 6 cups of lemonade concentrate and 10.5 cups of water He can make 16.5 cups of lemonade.
Question 16.
Multistep The ratio of North American butterflies to South American butterflies at a butterfly park is 5:3. The ratio of South American butterflies to European butterflies is 3:2. There are 30 North American butterflies at the butterfly park.
a. How many South American butterflies are there?
Answer:
Given ratio:
5 : 3 = \(\frac{5}{3}\)
The number of North American butterflies is 30 so the equation of proportion becomes:
\(\frac{5}{3}=\frac{30}{n}\)
Where n is the number of South American butterflies. Solve for n:
n = \(\frac{3}{5}\) × 30 = 18
There are 18 South American butterflies.
b. How many European butterflies are there?
Answer:
Given ratio:
3 : 2 = \(\frac{3}{2}\)
The number of South American butterflies is 18 so the equation of proportion becomes:
\(\frac{3}{2}=\frac{18}{y}\)
Where y is the number of European butterflies. Solve for y:
y = \(\frac{2}{3}\) × 18 = 12
There are 12 European butterflies.
Question 17.
Sinea and Ren are going to the carnival next week. The table shows the amount that each person spent on snacks, games, and souvenirs the last time they went to the carnival.
im – 7
a. Sinea wants to spend money using the same ratios as on her last trip to the carnival. If she spends $26 on games, how much will she spend on souvenirs?
Answer:
It can be seen that if she is spending $26 on games. then she is using \(\frac{26}{8}\) = 3.25 times the amount of money she used last time, so multiply the amount of money in each category with 3.25 to evaluate the amount of money to be spent this time on each category, therefore: 5 × 3.25 = $16.25 will be spent on games and 12 × 3.25 = $39 will be spent on souvenirs.
b. Ren wants to spend money using the same ratios as on his last trip to the carnival. If he spends $5 on souvenirs, how much will he spend on snacks?
Answer:
It can be seen that if he is spending $5 on souvenirs, then he is using \(\frac{5}{20}\) = 0.25 times the amount of money he used last time, so multiply the amount of money in each category with 0.25 to evaluate the amount of money to be spent this time on each category, therefore: 10 × 0.25 = $2.5 will be spent on snacks and 8 × 0.25 = $2 will be spent on games.
c. What If? Suppose Sinea and Ren each spend $40 on snacks, and each person spends money using the same ratios as on their last trip. Who spends more on souvenirs? Explain.
Answer:
It can be seen that if Sinea is spending $10 on snacks, then she is using \(\frac{40}{5}\) = 8 times the amount of money she used last time. so multiply the amount of money spent on souvenirs with 8 to evaluate the amount of money to be spent on souvenirs this time, therefore: 12 × 8 = $ 96 will be spent on souvenirs.
It can be seen that if Ren is spending $40 on snacks, then he is using \(\) = 4 times the amount of money lie used last time, so multiply the amount of money spent on souvenirs with 4 to evaluate the amount of money to be spent on souvenirs this time. therefore: 20 × 4 = $80 will be spent on souvenirs. Since 96 > 8, Sinea spends more on souvenirs.
H.O.T. Focus On Higher Order Thinking
Question 18.
Communicate Mathematical Ideas Explain why the ratio 2 to 5 is different from the ratio 5 to 2 if both represent the ratio of cats to dogs.
Answer:
In the first case, ratio of cats to dogs is:
\(\frac{\text { cats }}{\text { dogs }}=\frac{2}{5}\)
If there are 10 cats, let us find out how many dogs there are.
\(\frac{10}{\text { dogs }}=\frac{2}{5}\)
Multiply \(\frac{2}{5}\) with \(\frac{5}{5}\)
\(\frac{10}{\text { dogs }}=\frac{2}{5} \cdot \frac{5}{5}\)
\(\frac{10}{{dogs}}=\frac{10}{25}\)
There are 25 dogs.
In the second case, ratio of cats to dogs is:
\(\frac{\text { cats }}{\text { dogs }}=\frac{5}{2}\)
If there are 10 cats, Let us find out how many dogs there are.
\(\frac{10}{\text { dogs }}=\frac{5}{2}\)
Multiply \(\frac{5}{2}\) with \(\frac{2}{2}\)
\(\frac{10}{\text { dogs }}=\frac{5}{2} \cdot \frac{2}{2}\)
\(\frac{10}{{dogs}}=\frac{10}{4}\)
There are 4 dogs.
If there are 10 cats, in the first case, there are 25 dogs, while in the second case there are 4 dogs.
Question 19.
Analyze Relationships How is the process of finding equivalent ratios like the process of finding equivalent fractions?
Answer:
The 2 processes are identical, because a ratio is actually another representation of a fraction itself, the only difference that the numerator and denominator of a ratio represent a relation between the 2 given quantities.
A ratio is a representation of a fraction.
Question 20.
Explain the Error Tina says that 6:8 is equivalent to 36:64. What did Tina do wrong?
Answer:
She has multiplied both the numbers with 2 different numbers instead of the same. Here 6 : 8 can be equal to 36 : 48 or 48 : 64 but not 36 : 64.