Refer to our Texas Go Math Grade 6 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 6 Lesson 6.1 Answer Key Multiplying Integers.
Texas Go Math Grade 6 Lesson 6.1 Answer Key Multiplying Integers
Texas Go Math Grade 6 Lesson 1.1 Explore Activity Answer Key
Mu1tiplying integers Using a Number Line
You can use a number line to see what happens when you multiply a positive number by a negative number.
(A) Henry made three withdrawals of $2 each from his savings account.
What was the change in his balance?
Find 3(- 2).
To graph – 2, you would start at 0 and move __________ units to the left.
3(- 2) means ( __________ ) + ( __________ ) + ( __________ ).
To graph 3(- 2), start at 0 and move
2 units to the left __________ times.
The result is __________ .
The change in Henry’s balance was __________ .
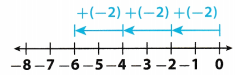
(B) Lisa plays a video game in which she loses points. She loses 3 points 2 times. What is her score?
Find 2(- 3).
2(- 3) means ( _____________ ) + ( _____________ ).
Show this on the number line. _________________________
Lisa has a score of _____________ .
![]()
RefIect
Question 1.
What do you notice about the product of two integers with different signs?
Answer:
The product of two integers with different signs is negative integer.
You can get the product using number line. Start at 0 and move to the left to represent multiplication of positive integer by negative integer.
Question 2.
What do you notice about the sign of the product of two negative integers?
Answer:
When you multiply two negative integers, the sign of the product would be plus (+).
If you use counters to find the product, counters that represent the result are positive so the sign of the result is plus(+).
Question 3.
Make a Conjecture What can you conclude about the sign of the product of two integers with the same sign?
Answer:
The sign of product of two integers with same sign is plus (+).
Use counters to represent the product of two integers, both positive or both negative.
You get all positive counters that represent the product so the result is positive.
Your Turn
Find each Product.
Question 4.
– 3(5) ________________
Answer:
First determine if the product will be positive or negative
Since – 3 is negative and 5 is positive (they have opposite signs), the product will be negative.
Then, multiply absolute values of given integers:
|- 3| = 3 and |5| = 5
3 × 5 = 15
the resuLt is 15 or – 15, depending on signs of given integers.
Product is negative so final result is – 15.
Find the sign of the product, multiply absolute values of integers and add minus if the sign of product is minus (-).
Question 5.
(- 10) (- 2) ________________
Answer:
First, determine if the product will be positive or negative
Since – 10 is negative and – 2 is negative (they have the same sign), the product will be positive.
Then, multiply absolute values of given integers:
|- 10| = 10 and |- 2| = 2
10 × 2 = 20
The result is 20 or – 20, depending on signs of given integers.
Product is positive so final result is 20.
Find the sign of the product, multiply absolute values of integers and add minus if the sign of product is minus (-).
Question 6.
7(- 6) ________________
Answer:
First, determine if the product will be positive or negative
Since 7 is positive and – 6 is negative (they have opposite signs), the product will be negative.
Then, multiply absolute values of given integers:
|7| = 7 and |- 6| = 6
7 × 6 = 42
The result is 42 or – 42, depending on signs of given integers.
Product is negative so final result is – 42.
Find the sign of the product, multiply absolute values of integers and add minus if the sign of product is minus (-).
Question 7.
0(- 22) ________________
Answer:
The product is 0
When you multiply any integer with 0, the result you get is 0.
Question 8.
(- 15) (- 3) ________________
Answer:
First, determine if the product will be positive or negative
Since – 15 is negative and – 3 is negative (they have the same sign), the product wilt be positive.
Then, multiply absolute values of given integers:
|- 15| = 15 and |- 3| = 3
15 × 3 = 45
The result is 45 or – 45, depending on signs of given integers.
Product is positive so final result is 45.
Find the sign of the product, multiply absolute values of integers and add minus if the sign of product is minus (-).
Question 9.
8(4) ________________
Answer:
First, determine if the product will be positive or negative
Since 8 is positive and 4 is positive (they have the same sign), the product wilt be positive.
Then, multiply absolute values of given integers:
|8| = 8 and |4| = 4
8 × 4 = 32
The result is 32 or – 32, depending on signs of given integers.
Product is positive so final result is 32.
Find the sign of the product, multiply absolute values of integers and add minus if the sign of product is minus (-).
Texas Go Math Grade 6 Lesson 6.1 Guided Practice Answer Key
Find each product.
Question 1.
– 1(9) ________________
Answer:
First, determine if the product will be positive or negative
Since – 1 is negative and 9 is positive (they have opposite signs), the product will be negative.
Then, multiply absolute values of given integers
|- 1| = 1 and |9| = 9
1 × 9 = 9
The result is 9 or – 9, depending on signs of given integers.
Product is negative so final result is – 9.
Find the sign of the product, multiply absolute values of integers and add minus if the sign of product is minus (-).
Question 2.
14(- 2) ________________
Answer:
First determine if the product will be positive or negative
Since 14 is positive and – 2 is negative (they have opposite signs), the product will be negative.
Then, multiply absolute values of given integers:
|14| = 14 and |- 2| = 2
14 × 2 = 28
The result is 28 or – 28, depending on signs of given integers.
Product is negative so final result is – 28.
Find the sign of the product, multiply absolute values of integers and add minus if the sign of product is minus (-).
Question 3.
(- 9) (- 6) ________________
Answer:
First determine if the product will be positive or negative
Since – 9 is negative and – 6 is negative (they have the same sign), the product will be positive.
Then, multiply absolute values of given integers:
|- 9| = 9 and |- 6| = 6
9 × 6 = 54
The result is 54 or – 54, depending on signs of given integers.
Product is positive so final result is 54.
Find the sign of the product, multiply absolute values of integers and add minus if the sign of product is minus (-).
Question 4.
(- 2) (50) ________________
Answer:
First, determine if the product will be positive or negative
Since – 2 is negative and 50 is positive (they have opposite signs), the product will be negative.
Then, multiply absolute values of given integers:
|- 2| = 2 and |50| = 50
2 × 50 = 100
The result is 100 or – 100, depending on signs of given integers.
Product is negative so final result is – 100.
Find the sign of the product, multiply absolute values of integers and add minus if the sign of product is minus (-).
Question 5.
(- 4) (15) ________________
Answer:
First, determine if the product will be positive or negative
Since – 4 is negative and 15 is positive (they have opposite signs), the product will be negative.
Then, multiply absolute values of given integers:
|- 4| = 4 and |15| = 15
4 × 15 = 60
The result is 60 or – 60, depending on signs of given integers.
Product is negative so final result is – 60.
Find the sign of the product, multiply absolute values of integers and add minus if the sign of product is minus (-).
Question 6.
– 18(0) ________________
Answer:
The product is 0
When you multiply any integer with 0, the result you get is 0.
Question 7.
(- 7) (- 7) ________________
Answer:
First, determine if the product will be positive or negative
Since – 7 is negative and – 7 is negative (they have the same sign), the product will be positive.
Then, multiply absolute values of given integers:
|- 7| = 7 and |- 7| = 7
7 × 7 = 49
The result is 49 or – 49, depending on signs of given integers.
Product is positive so final result is 49.
Find the sign of the product, multiply absolute values of integers and add minus if the sign of product is minus (-).
Question 8.
– 15 (9) ________________
Answer:
First, determine if the product will be positive or negative
Since – 15 is negative and 9 is positive (they have opposite signs), the product will be negative.
Then, multiply absolute values of given integers:
|- 15| = 15 and |9| = 9
15 × 9 = 135
The result is 135 or -135, depending on signs of given integers.
Product is negative so final result is – 135
Find the sign of the product, multiply absolute values of integers and add minus if the sign of product is minus (-).
Question 9.
(8) (- 12) ________________
Answer:
First, determine if the product will be positive or negative
Since 8 is positive and – 12 is negative (they have opposite signs), the product will be negative.
Then, multiply absolute values of given integers:
|8| = 8 and |- 12| = 12
8 × 12 = 96
The result is 96 or – 96, depending on signs of given integers.
Product is negative so final result is – 96.
Find the sign of the product, multiply absolute values of integers and add minus if the sign of product is minus (-).
Question 10.
– 3(- 100) ________________
Answer:
First, determine if the product will be positive or negative
Since – 3 is negative and – 100 is negative (they have the same sign), the product will be positive.
Then, multiply absolute values of given integers:
|- 3| = 3 and |- 100| = 100
3 × 100 = 300
The result is 300 or – 300, depending on signs of given integers.
Product is positive so final result is 300.
Find the sign of the product, multiply absolute values of integers and add minus if the sign of product is minus (-).
Question 11.
0(- 53) ________________
Answer:
The result is 0
When you multiply any integer with 0, the result you get is 0.
Question 12.
– 6(32) ________________
Answer:
First, determine if the product will be positive or negative
Since – 6 is negative and 32 is positive (they have opposite signs), the product will be negative.
Then, multiply absolute values of given integers.
|- 6| = 6 and |32| = 32
6 × 32 = 192
The result is 192 or – 192, depending on signs of given integers.
Product is negative so final result is – 192.
Find the sign of the product, multiply absolute values of integers and add minus if the sign of product is minus (-).
Question 13.
Flora made 7 withdrawals of $75 each from her bank account. What was the overall change in her account?
Answer:
Use negative integer to represent one withdrawal. The expression you get is:
7(- 75)
To find the value of the expression, determine if the product will be positive or negative
Since 7 is positive and 75 is negative (they have opposite signs), the product will be negative.
Then, multiply absolute values of given integers:
|7| = 7 and |75| = 75
7 × 75 = 525
The result is 525 or – 525, depending on signs of given integers.
Product is negative so final result is – 525.
The overall change in Flora’s account is $ – 525.
Find the sign of the product, multiply absolute values of integers and add minus if the sign of product is minus (-).
Question 14.
A football team lost 5 yards on each of 3 plays. Explain how you could use a number line to find the team’s change in field position after the 3 plays.
Answer:
The expression:
3(- 5)
represents the team’s change in field position
Use the number line to graph 3(- 5).
Start at 0 and move 5 units to the left 3 times to find the product
Read the result from number line.
Number line:
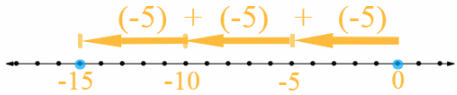
The team’s change in field position is – 15 because it is 15 units left from 0 on the number line.
The team’s change in field position is – 15.
Start at 0 and move 5 units to the left 3 times to find the product and read the result from number line.
Question 15.
The temperature dropped 2 °F every hour for 6 hours. What was the total number of degrees the temperature changed in the 6 hours?
Answer:
Use negative integer to represent the temperature change because the temperature dropped every hour.
The expression:
6 (-2)
models the temperature change.
Use the number tine to graph 6(-2).
Start at 0 and move 2 units to the left 6 times to find the product.
The result is 12 units left from 0 on the number line so the product is – 12.
The temperature dropped 12 degrees in 6 hours
Start at 0 and move 2 units to the left 6 times on number line to find the result.
Question 16.
The price of one share of Acme Company declined $5 per day for 4 days in a row. How much did the price of one share change in total after the 4 days?
Answer:
Use negative integer to represent change of price per day because it declined each day.
The expression: 4(- 5)
models the change of the price.
Use number line to graph 4(- 5).
Start at 0 and move 5 units to the left 4 times to find the product.
The result is 20 units left from 0 on the number line so the product is – 20
The price of one share declined $20 after 4 days.
Question 17.
A mountain climber climbed down a cliff 50 feet at a time. He did this 5 times in one day. What was the overall change in his elevation?
Answer:
Use negative integer to represent change at a time because he climbed down
The expression:
5(- 50)
models the overall change in climbers elevation
Use number line to graph 5(- 50).
Start at 0 and move 50 units to the left 5 times to find the product
The result is 250 units left from 0 on the number tine so the product is – 250.
Overall change in climber’s elevation was – 250 feet
Essential Question Check-In
Question 18.
Explain the process for finding the product of two integers.
Answer:
First determine if the product wilL be positive or negative
If integers have the same sign (both positive or both negative), the product will be positive.
If integers have opposite signs (one positive and another negative), the product will be negative.
Then, multiply absolute values of given integers:
|a| × |b| = c
The result is c or – c, depending on signs of given integers.
If product is positive, final result is c and if it is negative, final result is – c.
If you multiply any integer with 0, the product you get is 0.
Find the sign of the product (the same sign of integers then +, opposite signs of integers then -), multiply absolute value of integers and add minus if the sign of product is minus (-)
Question 19.
Critique Reasoning Lisa used a number line to model 2(3). Does her number line make sense? Explain why or why not.
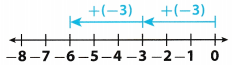
Answer:
Lisa’s number line is incorrect.
She moved to the left on the number line so that would represent the product: 2(- 3)
To model: 2(3)
using number line, she needed to start at 0 and move 3 units to the right 2 times (see number line below).
The product is 6 because it is 6 units right from 0 on number line
Number line:

Lisa’s number line is incorrect.
To model 2(3) using number line, she needed to start at 0 and move 3 units to the right 2 times.
Question 20.
Represent Real-World Problems Mike got on an elevator and went down 3 floors. He meant to go to a lower level, so he stayed on the elevator and went down 3 more floors. How many floors did Mike go down altogether?
Answer:
Use negative integer to represent number of floors he went down at once.
The expression you get is:
2 (- 3)
First, determine if the product will be positive or negative
Since 2 is positive and – 3 is negative (they have opposite signs), the product will be negative.
Then, multiply absolute values of given integers:
|2| = 2 and |- 3| = 3
2 × 3 = 6
The result is 6 or – 6, depending on signs of given integers
Product is negative so final result is – 6.
Mike went down 6 floors
Find the sign of the product, multiply absolute values of integers and add minus if the sign of product is minus (-).
Solve. Show your work.
Question 21.
When Brooke buys lunch at the cafeteria, money is withdrawn from a lunch account. The table shows amounts withdrawn in one week. By how much did the amount in Brooke’s lunch account change by the end of that week?
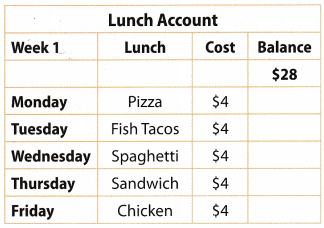
Answer:
Use negative integer to represent each amount because the money is withdrawn.
Since the same amount ¡s withdrawn every day, you can find the product: 5 (- 4)
First, determine if the product will be positive or negative
Since 5 is positive and – 4 is negative (they have opposite signs), the product will be negative.
Then, multiply absolute values of given integers:
|5| = 5 and |- 4| = 4
5 × 4 = 20
The result is 20 or – 20, depending on signs of given integers.
Product is negative so the final result is – 20.
The amount in Brooke’s account changed by $ – 20.
Find the sign of the product, multiply absolute values of integers and add minus if the sign of product is minus (-).
Question 22.
Adam is scuba diving. He descends 5 feet below sea level. He descends the same distance 4 more times. What is Adam’s final elevation?
Answer:
Adam descends 5 times the same distance, 5 feet, so the expression that models his elevation is: 5(- 5)
First, determine if the product will be positive or negative.
Since 5 is positive and – 5 is negative (they have opposite signs), the product will be negative.
Then, multiply absolute values of given integers:
|5| = 5 and |- 5| = 5
5 × 5 = 25
The result is 25 or – 25, depending on signs of given integers.
Product is negative so final result is – 25.
Adam’s final elevation b – 25 feet or 25 feet below sea level.
Find the sign of the product, multiply absolute values of integers and add minus if the sign of product is minus (-).
Question 23.
The price of jeans was reduced $6 per week for 7 weeks. By how much did the price of the jeans change over the 7 weeks?
Answer:
Since the price was reduced $6 per week. the expression that models change of price is:
7(- 6)
First determine if the product will be positive or negative.
Since 7 is positive and – 6 is negative (they have opposite signs), the product will be negative.
Then, multiply absolute values of given integers:
|7| = 7 and |- 6| = 6
7 × 6 = 42
The result is 42 or – 42. depending on signs of given integers.
Product is negative so final result is – 42.
The price changed by $ – 42.
Find the sign of the product, multiply absolute values of integers and add minus if the sign of product is minus (-).
Question 24.
Casey uses some of his savings on batting practice. The cost of renting a batting cage for 1 hour is $6. He rents a cage for 9 hours in each of two months. What is the change in Casey’s savings after two months?
Answer:
First, calculate the amount of savings that Casey spends first month. Use negative integer to represent the cost of renting for 1 hour.
The expression you get is:
9(- 6)
Determine if the product wilt be positive or negative
Since 9 is positive and – 6 is negative (they have opposite signs), the product will be negative
Multiply absolute values of given integers:
|9| = 9 and |- 6| = 6
9 × 6 = 54
The result is 54 or – 54, depending on signs of given integers.
Product is negative so result is – 54
Now, multiply that result with 2 to calculate the change in his savings after 2 months.
The expression you get is:
2(- 54)
Determine if the product will be positive or negative
Since 2 ¡s positive and – 54 is negative (they have opposite signs), the product will be negative.
Multiply absolute values of given integers:
|2| = 2 and |- 54| = 54
2 × 54 = 108
The result is 108 or – 108, depending on signs of given integers.
Product is negative so result is – 108.
The change in Casey’s savings is $ – 108.
The change in Casey’s savings after 2 months is $ – 108.
Multiply 9(-6) to find the change for one month and then multiply that result with 2 to find the change in savings after two months.
Question 25.
Volunteers at Sam’s school use some of the student council’s savings for a special project. They buy 7 backpacks for $8 each and fill each backpack with paper and pens that cost $5. By how much did the student council’s savings change because of this project?
Answer:
Use negative integers to model by how much the savings changed.
They pay each backpack $8 and paper and pens for each backpack cost $5
so the product
7(- 8 + (- 5))
shows how much this project cost.
First, find the sum in the brackets using rules for adding integers:
7(- 13)
Then, determine if the product will be positive or negative.
Since 7 is positive and – 13 is negative (they have opposite signs), the product will be negative.
Multiply absolute values of given integers:
|7| = 7 and |- 13| = 13
7 × 13 = 91
The result is 91 or – 91, depending on signs of given integers.
Product is negative so final result is – 91.
Student council’s savings changed by $ – 91.
Find the sum in brackets using rules for adding integers and then calculate the product using rules for multiplying integers.
Question 26.
Communicate Mathematical Ideas Describe a real-world situation that can be represented by the product 8(- 20). Then find the product and explain what the product means in terms of the real-world situation.
Answer:
Nick wants to clean the pool so he needs to drain water to a certain level. He drains 20 cm of water at once and he repeats that procedure another 7 times. Find out how much the water level changes after the draining.
Since the water level falls, use negative integer to represent water level that is drained at once. The expression you get is:
8(- 20)
First, determine if the product will be positive or negative
Since 8 is positive and – 20 is negative (they have opposite signs, the product will be negative.
Then, multiply absolute values of given integers:
|8| = 8 and |- 20| = 20
8 × 20 = 160
The result is 160 or – 160, depending on signs of given integers.
Product is negative so final result is – 160
The water level is 160 cm lower than before draining. In another way, change of water level is – 160 cm.
Nick wants to clean the pool so he needs to drain water to a certain level.
He drains 20 cm of water at once and he repeats that procedure another 7 times. Find out how much the water level changes after the draining.
The water level is 160 cm lower than before draining. In another way, change of water level is – 160 cm.
Question 27.
What If? The rules for multiplying two integers can be extended to a product of 3 or more integers. Find the following products by using the Associative Property to multiply 2 numbers at a time.
a. 3(3)(- 3) ________________
Answer:
3(3) (- 3)
Use Associative Property and rules for multiplying integers to simplify multiplication:
(3 × 3) (- 3)
9(- 3)
Find the final result using rules for multiplying integers:
9 × (- 3) = – 27
3(3) (- 3) = – 27
b. 3(- 3)(- 3) ________________
Answer:
3(3) (- 3)
Use Associative Property and rules for multiplying integers to simplify multiplication:
3((- 3) × (- 3))
3(9)
Find the final result using rules for multiplying integers:
3 × 9 = 27
3(- 3) (- 3) = 27
c. – 3(- 3)(- 3) ________________
Answer:
– 3 (-3) (-3)
Use Associative Property and rules for multiplying integers to simplify multiplication:
((-3) × (-3)) (-3)
9(- 3)
Fina the final result using rules for multiplying integers:
9 × (-3) = -27
-3(-3)(-3) = -27
d. 3(3)(3) (- 3) ________________
Answer:
– 3 (-3) (-3)
Use Associative Property and rules for multiplying integers to simplify multiplication:
(3 × 3) (3 × (- 3))
9 (- 9)
Fina the final result using rules for multiplying integers:
9 × (- 9) = – 81
3(3) (3) (- 3) = – 81
e. 3(3) (- 3) (- 3) ________________
Answer:
3(3) (- 3) (- 3)
Use Associative Property and rules for multiplying integers to simplify multiplication:
(3 × 3)((- 3) × (- 3))
9(9)
Find the final result using rules for multiplying integers:
9 × 9 = 81
3(3) (- 3) (- 3) = 81
f. 3(3) (- 3) (- 3) (- 3) ________________
Answer:
3(3) (- 3) (- 3)
Use Associative Property and rules for multiplying integers to simplify multiplication:
(3 × (- 3)) ((- 3) × (- 3))
– 9 (9)
Find the final result using rules for multiplying integers:
– 9 × 9 = 81
3(- 3) (- 3) (- 3) = – 81
g. Make a Conjecture Based on your results, complete the following statements:
When a product of integers has an odd number of negative factors,
then the sign of the product is ____________ .
When a product of integers has an even number of negative factors,
then the sign of the product is ____________ .
Answer:
Based on examples a), C), d) and f), first requested word is minus(-).
Based on examples b) and e), second requested word is plus(+).
H.O.T. Focus ON Higher Order Thinking
Question 28.
Multiple Representations The product of three integers is – 3. Determine all of the possible values for the three factors.
Answer:
One possible combination is:
1(1) (-3)
Use Associative Property and rules for multiplying integers to check the result:
(1 × 1) (- 3)
1 × (- 3) = – 3
Another possible combination is:
1(- 1) (3)
Use Associative Property and rules for multiplying integers to check the result:
(1 × (-1) (3)
– 1 × 3 = – 3
You can get combination
– 1(1)(3)
by using Commutative Property on the previous combination so the result is the same as the previous one, – 3.
Possible combinations are 1(1)(- 3) and 1(- 1)(3).
You can get one more combination by using Commutative Property, – 1(1)(3).
Question 29.
Analyze Relationships When is the product of two nonzero integers less than or equal to both of the two factors?
Answer:
There are two cases in which the product of two integers (both nonzero) is less than or equal to both of those two numbers.
First possibility is that one factor is negative and another factor is positive.
Second possibility is that both of the factors are equal to 1.
You can check first possibility on examples (use rules for multiplying integers to find products):
4 × (- 5) = – 20
Compare the product with both factors:
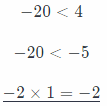
Compare the product with both factors:
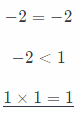
Compare the product with both factors:
![]()
Question 30.
Justify Reasoning The sign of the product of two integers with the same sign is positive. What is the sign of the product of three integers with the same sign? Explain your thinking.
Answer:
The sign of the product of three integers with the same sign depends on sign of those integers.
If integers are positive, the sign of the product would be plus ( + )
If integers are negative, the sign of the product would be minus ( – )
Check it on the product of three integers with the same sign:
a(b) (c)
Find the product of first and second factor:
a × b
You will get positive result because the sign of the product of two integers with the same sign is plus (+).
If the third factor, c, is positive, final result would be positive (because the sign of the product of two integers with the same sign is plus (+)).
If c is negative, final result would be negative (because the sign of the product of two integers with opposite signs is minus (-)).
The sign of the product of three integers with the same sign depends on sign of those integers.
If integers are positive, the sign of the product would he plus (+).
If integers are negative, the sign of the product would be minus (-).