Refer to our Texas Go Math Grade 6 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 6 Lesson 14.4 Answer Key Representing Algebraic Relationships in Tables and Graphs.
Texas Go Math Grade 6 Lesson 14.4 Answer Key Representing Algebraic Relationships in Tables and Graphs
Essential Question
How can you use verbal descriptions, tables, and graphs to represent algebraic relationships?
Texas Go Math Grade 6 Lesson 14.4 Explore Activity Answer Key
Explore Activity 1
Representing Algebraic Relationships
Angie’s walking speed is 5 kilometers per hour, and May’s is 4 kilometers per hour. Use tables and graphs to show how the distance each girl walks is related to time.
A. For each girl, make a table comparing time and distance.

B. For each girl, make a graph showing her distance y as it depends on time x. Plot points from the table and connect them with a line.
Reflect
Question 1.
Analyze Relationships How can you use the tables to determine which girl is walking faster? How can you use the graphs?
Answer:
It can be seen from the table, that after 2 hours Angie has covered 10 miles white Mary has only covered 8 miles. This implies that Angie is walking faster than Mary.
The graph of Angie will be steeper than that of Mary’s indicating a greater rate of change of distance with respect
to time.
Explore Activity 2
Writing an Equation from a Graph
Cherise pays the entrance fee to visit a museum, then buys souvenirs at the gift shop. The graph shows the relationship between the total amount she spends at the museum and the amount she spends at the gift shop. Write an equation to represent the relationship.

A. Read the ordered pairs from the graph. Use them to complete a table comparing total spent y to amount spent at the gift shop x.
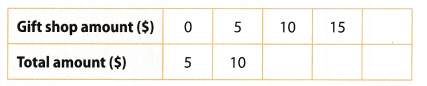
B. What is the pattern in the table?
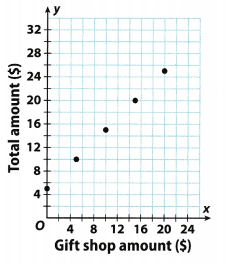
C. Write an equation that expresses the total amount y in terms of the gift shop amount x.
Reflect
Question 2.
Identify the dependent and independent quantities in this situation.
Answer:
The money spent in the gift shop is the independent variable while the total amount depending on the gift shop amount is the independent variable.
Question 3.
Draw a line through the points in the graph. Find the point that represents Cherise spending $25 at the gift shop. Use this point to find the total she would spend if she spent $25 at the gift shop. Then use your equation from C to verify your answer.
Answer:
On the following picture there is a line through the given points in the graph.
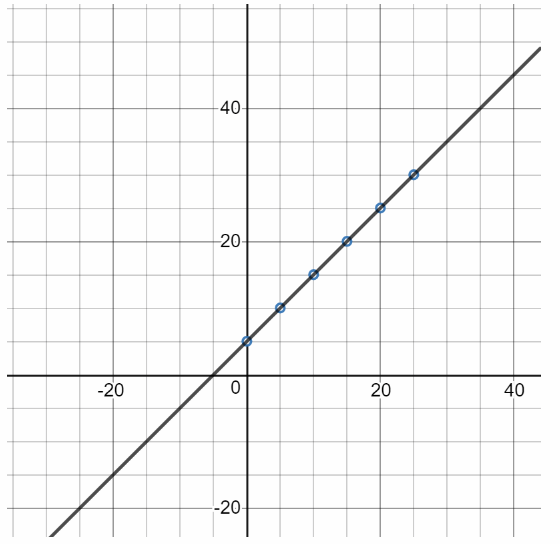
From the graph we can see that if she spent $25 at the gift shop, she would total spend $30.
Really, equation from C is y = x + 5 where y represent total amount and x represent gift shop amount. We will Substitute 25 for x in this equation and get:
y = 25 + 5 = 30
So, we verified our answer.
$30
Question 4.
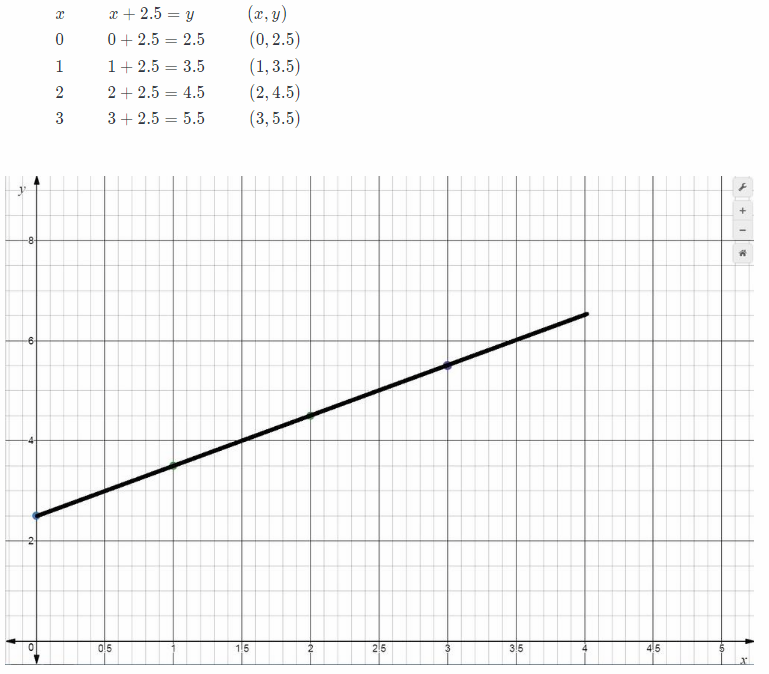
Graph y = x + 2.5.

Answer:
Solution to this example is given below
y = x + 2.5
Make a table of values. Choose some values for x and use the equation to find the corresponding values for y.
Plot the ordered pairs from the table.
Draw a line through the plotted points to represent all of the ordered pair solutions of the equation.
Texas Go Math Grade 6 Lesson 14.4 Guided Practice Answer Key
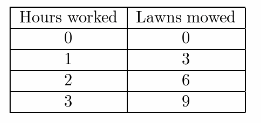
Frank mows lawns in the summer to earn extra money. He can mow 3 lawns every hour he works. (Explore Activity 1 and Explore Activity 2)
Question 1.
Make a table to show the relationship between the number of hours. Frank works, x, and the number of lawns he mows, y. Graph the relationship and write an equation.

Answer:
Using given information we get the following table:
One way to determine relationship between the number of hours Frank works, x, and the number of lawns he mows, y is to find their quotient:
\(\frac{3}{1}\) = 3
\(\frac{6}{2}\) = 3
\(\frac{9}{3}\)3
So, required relationship is:
y = 3x
Now, we will graph previous equation.

y = 3x
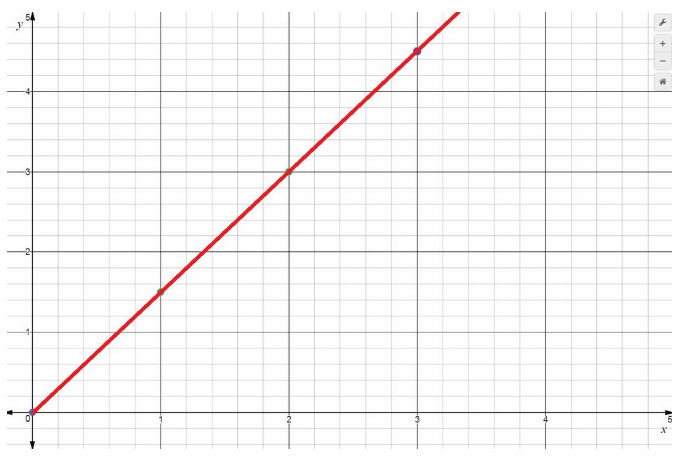
Graph y = 1.5x. (Example 1)
Question 2.
Make a table to show the relationship.

Answer:
Solution to this example is given below
y = 1.5x
Make a table of values. Choose some values or x and use the equation to find the corresponding values for y.
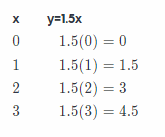
Question 3.
Plot the points and draw a line through them.
Answer:
Solution to this example is given below
y = 1.5x
Plot the ordered pairs from the table.
Draw a line through the plotted points to represent all of the ordered pair solutions of the equation.
Essential Check-in
Question 4.
How can a table represent an algebraic relationship between two variables?
Answer:
A table is a collection of ordered pairs which show a certain algebraic relationship between two variables. This can be a multiplicative one where y = or an additive one where y = x + k. The table enables the readers to determine this algebraic relationship using the ordered pairs in the table.
Texas Go Math Grade 6 Lesson 14.4 Independent Practice Answer Key
Students at Mills Middle School are required to work a certain number of community service hours. Students may work additional hours beyond the requirement.
Question 5.
Read the ordered pairs from the graph to make a table.

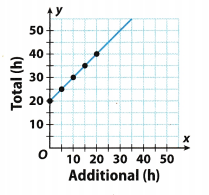
Answer:
x from the graph Corresponding value of y from the graph
0 20
5 25
10 30
15 35
20 40
Question 6.
Write an equation that expresses the total hours in terms of the additional hours.
Answer:
From the study of the graph as well as the table, it can be seen that total hours when additional hours is equal to 0 is 20, this implies that the total number of hours is the sum of 20 and additional hours, so the equation for the relation between additional hours z and total hours y, becomes: y = x + 20
y = x + 20.
Question 7.
Analyze Relationships How many community service hours are students required to work? Explain.
Answer:
The students required to work 20 hours. This is seen when 0 additional hours are worked, the total is 20 hours.
The students required to work 20 hours.
Beth is using a map. Let x represent a distance in centimeters on the map. To find an actual distance y in kilometers, Beth uses the equation y = 8x.
Question 8.
Make a table comparing a distance on the map to the actual distance.

Answer:
x y = 8x
0 y = 8(0) = O
1 y = 8(1) = 8
2 y = 8(2) = 16
3 y = 8(3) = 24
4 y = 8(4) = 32
5 y = 8(5) = 40
Question 9.
Make a graph that compares the map distance to the actual distance.
Answer:
On the following picture there is a graph that compares the map distance to the actual distance.
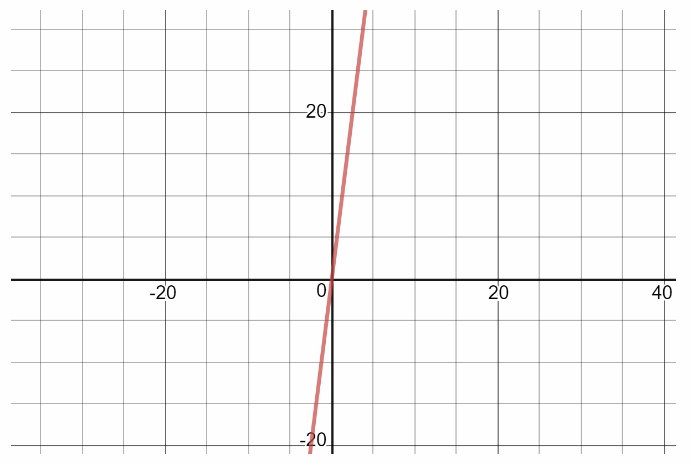
Graph y = 8x
Question 10.
Critical Thinking The actual distance between Town A and Town B is 64 kilometers. What is the distance on Beth’s map? Did you use the graph or the equation to find the answer? Why?
Answer:
Use of the equation here is preferable because the graph plotted does not contain the point where y = 64, therefore given equation:
y = 8x
Substitute the value of y ¡n the given equation:
64 = 8x
Solve for x:
x = \(\frac{64}{8}\) = 8
Town A and Town B are 8 centimeters apart on the map.
Question 11.
Multistep The equation y = 9x represents the total cost y for x movie tickets.
a. Make a table and a graph to represent the relationship between x and y.

Answer:
On the following picture there is a graph of the equation y = 9x.
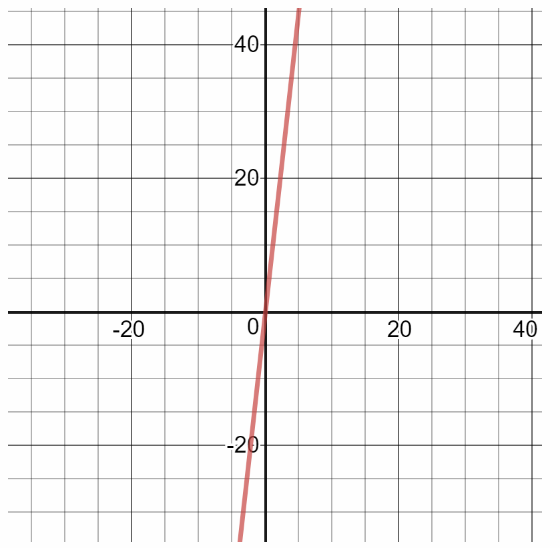
Also, there is the following table which represent the relationship between x and y:

b. Critical Thinking In this situation, which quantity is dependent and which is independent? Justify your answer.
Answer:
We can conclude that here dependent quantity is total, cost and independent quantity is number of tickets. We could conclude this because total cost depends of the number of tickets we bought
c. Multiple Representations Eight friends want to go see a movie. Would you prefer to use an equation, a table, or a graph to find the cost of 8 movie tickets? Explain how you would use your chosen method to find the cost.
Answer:
Here, the easiest way is to use an equation. We will substitute 8 for x in the equation and calculate y:
y = 9.8
y = 72
So, tickets for 8 movies will cost $72.
Texas Go Math Grade 6 Lesson 14.4 H.O.T. Focus On Higher Order Thinking Answer Key
Question 12.
Critical Thinking Think about graphing the equations y = 5x and y = x + 500. Which line would be steeper? Why?
Answer:
The steepness of a graph depends on its coefficient of x, the greater the value of the coefficient, the more steep its graph is. Here 5 < 1 so the graph of y = 5x will be steeper than that of y = x + 500.
y = 5x will have a steeper graph.
Question 13.
Persevere in Problem Solving Marcus plotted the points (0, 0), (6, 2), (18, 6), and (21, 7) on a graph. He wrote an equation for the relationship. Find another ordered pair that could be a solution of Marcus’s equation. Justify your answer.
Answer:
From the given ordered pairs, it can be seen that the value of y is \(\frac{2}{6}\) = \(\frac{6}{18}\) = \(\frac{7}{21}\) = \(\frac{1}{3}\); times that of its corresponding value of x, therefore if z = 24, then y = \(\frac{24}{3}\) = 8 so the ordered pair (24, 8) must also lie on this graph.
Question 14.
Error Analysis The cost of a personal pizza is $4. A drink costs $1. Anna wrote the equation y = 4x + 1 to represent the relationship between total cost y of buying x meals that include one personal pizza and one drink. Describe Anna’s error and write the correct equation.
Answer:
1 meal consists of a pizza for $4 and a drink for $1 so the total cost of 1 meal is $4 + $1 = $5. This implies that the cost of buying x meals will be y = 5x and not y = 4x + 1.