Refer to our Texas Go Math Grade 6 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 6 Lesson 14.3 Answer Key Writing Equations from Tables.
Texas Go Math Grade 6 Lesson 14.3 Answer Key Writing Equations from Tables
Essential Question
How can you use an equation to show a relationship between two variables?
Texas Go Math Grade 6 Lesson 14.3 Explore Activity Answer Key
Explore Activity
Writing an Equation to Represent a Real-World Relationship
Many real-world situations involve two variable quantities in which one quantity depends on the other. This type of relationship can be represented by a table. You can also use an equation to model the relationship.

The table shows how much Amanda earns for walking 1,2, or 3 dogs. Use the table to determine how much Amanda earns per dog. Then write an equation that models the relationship between number of dogs walked and earnings. Use your equation to complete the table.

A. For each column, compare the number of dogs walked and earnings. What is the pattern?
B. Based on the pattern, Amanda earns $ ___ for each dog she walks.
C. Write an equation that relates the number of dogs Amanda walks to the amount she earns. Let e represent earnings and d represent dogs.
D. Use your equation to complete the table for 5,10, and 20 walked dogs.
E. Amanda’s earnings depend on ____.
Reflect
Question 1.
What If? If Amanda changed the amount earned per dog to $11, what equation could you write to model the relationship between number of dogs walked and earnings?_____
Answer:
If Amanda changed the amount earned per dog to $11 then her total earning y is given by the equation; y = 11x.
y = 11x
Your Turn
For each table, write an equation that expresses y in terms of x.
Question 2.
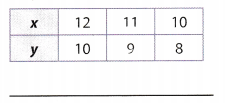
Answer:
Compare the x- and y-values to find a pattern.
Each y-value is 2 less than the corresponding x-value.
Use the pattern to write an equation expressing y in terms of x.
y = x – 2
y = x – 2 Final solution
y = x – 2
Question 3.
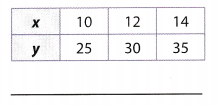
Answer:
Compare the x- and y-values to find a pattern.
Each x-value is 2.5 times the corresponding y-value.
Use the pattern to write an equation expressing y in terms of x.
y = 2.5x
y = 2.5x Final solution
y = 2.5x
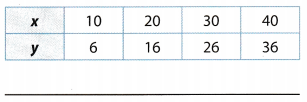
Question 4.
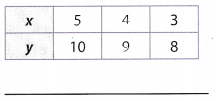
Answer:
Compare the x- and y-values to find a pattern.
Each y-value is 5 more than the corresponding x-value.
Use the pattern to write an equation expressing y in terms of x.
y = x + 5
y = x + 5 Final solution
y = x + 5
Question 5.
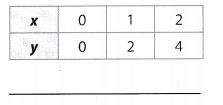
Answer:
Compare the x- and y-values to find a pattern.
Each x-value is 2 times the corresponding y-value.
Use the pattern to write an equation expressing y in terms of x.
y = 2x
y = 2x Final solution
y = 2x
Your Turn
Question 6.
When Ryan is 10, his brother Kyle is 15. When Ryan is 16, Kyle will be 21. When Ryan is 21, Kyle will be 26. Complete the table for Ryan and Kyle. Write and solve an equation to find Kyle’s age when Ryan is 52.
Answer:
Using all given informations for Ryan’s and Kyle’s ages. we get the following
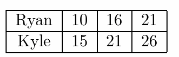
First we need to find What is relationship betWeeti Ryan’s and Kyle’s ages, let x1 be 10 and 2 be 16, because of this, y1 will be 15 and y2 will be 21.
We will use equation of line through those two points and get:
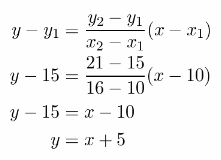
So, when Ryan is 52, that means y = 52. We will substitute it in previous equation where s represent ages of Kyle.
52 = x + 5
x = 47
So, Kyle will be at the age of 47 when Ryan is 52.
47
Texas Go Math Grade 6 Lesson 14.3 Guided Practice Answer Key
Write an equation to express y in terms of x.
Question 1.
Answer:
Compare the x- and y-values to find a pattern.
Each y-value is 4 less than the corresponding x-value.
Use the pattern to write an equation expressing y in terms of x.
y = x – 4
y = x – 4 Final solution
Question 2.
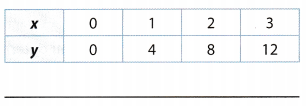
Answer:
Compare the x- and y-values to find a pattern.
Each y-value is 4 times less than the corresponding x-value.
Use the pattern to write an equation expressing y in terms of x.
y = 4x
y = 4x Final solution
Question 3.
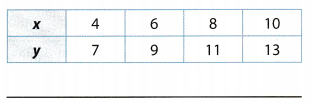
Answer:
Compare the x- and y-values to find a pattern.
Each y-value is 3 more than the corresponding x-value.
Use the pattern to write an equation expressing y in terms of x.
y = x + 3
y = x + 3 Final solution
Question 4.

Answer:
Compare the x- and y-values to find a pattern.
Each y-value is 6 times less than the corresponding x-value.
Use the pattern to write an equation expressing y in terms of x.
y = \(\frac{x}{6}\)
y = \(\frac{x}{6}\) = Final solution
Question 5.
Jameson downloaded one digital song for $1.35, two digital songs for $2.70, and 5 digital songs for $6.75. Complete the table. Write and solve an equation to find the cost to download 25 digital songs. (Example 2)

Number of songs = n; Cost = ____
The total cost of 25 songs is _____
Answer:
We have the following table:
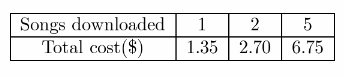
One way to determine realitonship between downloaded songs and total cost is to find their quotient:
\(\frac{1.35}{1}\) = 1.35
\(\frac{2.70}{2}\) = 1.35
\(\frac{6.75}{5}\) = 1.35
Let n represent number of songs and let p represent cost in $. According to previous result, we have the following relationship:\p1.35n\
Now, we will find the total cost of 25 songs using previous result and subtracting 25 for n:
p = 1.35 . 25
p = 33.75
So, the total cost of 25 songs is $ 33.75.
So, equation is correct.
p = 1.35n, p = 33.75
Essential Question Check-In
Question 6.
Explain how to use a table to write an equation that represents the relationship in the table,
Answer:
The ordered pairs in a table can be used to determine the equation of the relationship between the 2 variables.
Case 1: Check if each value of y is proportional to the corresponding value of x. If its true, then the equation is given by: y = kx where k is evaluated using the equation k = \(\frac{y}{x}\) using the ordered pairs.
Case 2: Check if each value of y is a units bigger (or smaller) than the corresponding value of x. If its true, then the equation is given by: y = x + a where a is evaluated using the equation a = y – x using the ordered pairs.
Texas Go Math Grade 6 Lesson 14.3 Independent Practice Answer Key
Question 7.
Vocabulary What does it mean for an equation to express y in terms of x?
Answer:
An equation to express y in terms of x means that the quantity y depends on the quantity x.
Question 8.
The length of a rectangle is 2 inches more than twice its width. Write an equation relating the length l of the rectangle to its width w.
Answer:
The length of a rectangle is 2 inches more than twice its width, then the equation for length of the rectangle is l = 2w + 2.
l = 2w + 2.
Question 9.
Look for a Pattern Compare the y-values in the table to the corresponding x-values. What pattern do you see? How is this pattern used to write an equation that represents the relationship between the x- and y-values?
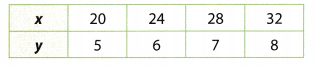
Answer:
Compare the x- and y-values to find a pattern.
Each y-value is 4 times less than the corresponding x-value
Use the pattern to write an equation expressing y in terms of x.
y = \(\frac{x}{4}\)
y = \(\frac{x}{4}\) Final solution
Question 10.
Explain the Error A student modeled the relationship in the table with the equation x = 4y. Explain the student’s error. Write an equation that correctly models the relationship.
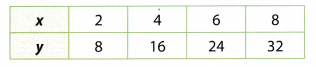
Answer:
Compare the x- and y-values to find a pattern.
Each y-value is 4 times the corresponding x-value.
Use the pattern to write an equation expressing y in terms of x.
y = 4x
y = 4x Final solution
Question 11.
Multistep Marvin earns $8.25 per hour at his summer job. He wants to buy a video game system that costs $206.25.
a. Write an equation to model the relationship between number of hours worked h and amount earned e.
Answer:
Marvin earns $8.25 per hour at his summer job. This implies that after working for h hours, he will earn e = 8.25h.
b. Solve your equation to find the number of hours Marvin needs to work in order to afford the video game system.
Answer:
He needs to raise S206.25 so substitute e = 206.25 and solve for h:
206.25 = 8.25h
Solve for h:
h = \(\frac{206.25}{8.25}\) = 25
Marvin needs to work for 25 hours to buy the video game.
Question 12.
Communicate Mathematical Ideas For every hour that Noah studies, his test score goes up 3 points. Explain which is the independent variable and which is the dependent variable. Write an equation modeling the relationship between hours studied h and the increase in Noah’s test score s.
Answer:
The independent variable here is the number of hours studied and the dependent variable here is the increase in test score. The 2 are related with the equation: S = h + 3
s = h + 3
Texas Go Math Grade 6 Lesson 14.3 H.O.T. Focus On Higher Order Thinking Answer Key
Question 13.
Make a Conjecture Compare the y-values in the table to the corresponding x-values. Determine whether there is an additive relationship or a multiplicative relationship between x and y. If possible, write an equation modeling the relationship. If not, explain why.
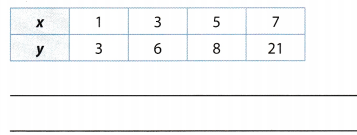
Answer:
No clear pattern is visible between the 2 variables shown. The value of y 2 more than the value of x in the first case but this pattern does not continue and the values of y are neither a multiple of x and a constant so the relationship shown can not be expressed by an equation.
No pattern exists between x and y.
Question 14.
Represent Real-World Problems Describe a real-world situation in which there is an additive or multiplicative relationship between two quantities. Make a table that includes at least three pairs of values. Then write an equation that models the relationship between the quantities.
Answer:
Case 1: The total cost y of x sandwiches if each sandwich costs $4 is a case of a multiplicative relationship which is given by the equation: y = 4x. Therefore, the ordered pairs are: (0, 0), (1, 4), (2, 8), (3, 12), (4, 16)… and so on.
Case 2: The total cost y of a boat rental for x hours if the rent of 1 hour is $1 plus a fixed cost of $15 is a case of a additive relationship which is given by the equation: y = x + 13. Therefore, the ordered pairs are: (0, 10), (1, 16), (2, 17), (3, 18), (4, 19)… and so on.
Question 15.
Critical Thinking Georgia knows that there is either an additive or multiplicative relationship between x and y. She only knows a single pair of data values. Explain whether Georgia has enough information to write an equation that models the relationship between x and y.
Answer:
A single pair of data values is not sufficient to determine the relation between x and y. At least 2 pairs of data values are required.