Refer to our Texas Go Math Grade 6 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 6 Lesson 14.1 Answer Key Graphing on the Coordinate Plane.
Texas Go Math Grade 6 Lesson 14.1 Answer Key Graphing on the Coordinate Plane
Essential Question
How do you locate and name points in the coordinate plane?
Reflect
Question 1.
If both coordinates of a point are negative, in which quadrant is the point located?
Answer:
If both coordinates of a point are negative, then this implies that the point lies in the third quadrant.
Third quadrant.
Question 2.
Describe the coordinates of all points in Quadrant 1.
Answer:
Both the x and y coordinates of all the points of Quadrant 1 are positive.
Question 3.
Communicate Mathematical Ideas Explain why (-3, 5) represents a different location than (3, 5).
Answer:
(-3, 5) lies in the 2nd quadrant while (3, 5) lies in the 1st quadrant. They are a mirror image of one another in the y-axis.
Your Turn
Identify the coordinates of each point. Name the quadrant where each point is located.
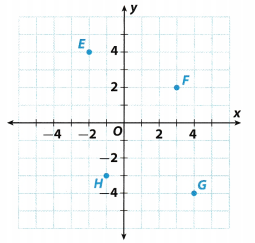
Question 4.
G ______
E _______
Answer:
Solution to this example is given below
Point G is 4 units right of the origin, and 4 units down. It has x-coordinate 4 and y-coordinate -4, written (4, -4). It is located in Quadrant IV
Point E is 2 units Left of the origin, and 4 units up. It has x-coordinate -2 and y-coordinate 4, ‘written (-2, 4). It is located in Quadrant II
G = (4, -4) : E = (2, -4) Final solution
G = (4, -4) : E = (2, -4)
Question 5.
F _____
H _____
Answer:
Solution to this example is given below
Point F is 3 units right of the origin, and 2 units up. It has x-coordinate 3 and y-coordinate 2, written (3, 2). It is located in Quadrant I.
Point H is 1 units left of the origin, and 3 units down It has x-coordinate -1 and y-coordinate -3, written (-1, -3). It is located in Quadrant III.
F = (3, 2) : H = (-1, -3) Final solution
F = (3, 2) : H = (-1, -3)
Your Turn
Graph and label each point on the coordinate plane.
Question 6.
P(-4, 2)
Answer:
Solution to this example is given below
Point P is 4 units left of the origin, and 2 units up. It has x-coordinate -4 and y-coordinate 2, written (-4, 2). It is located in Quadrant II.
P = (-4, 2) Final solution
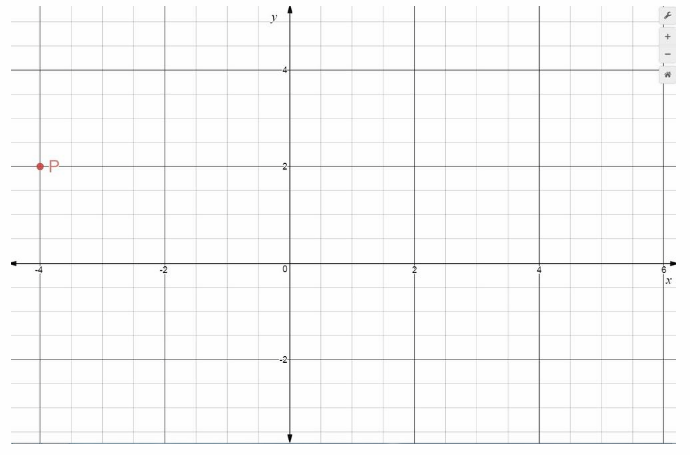
P = (-4, 2)
Question 7.
Q(3, 2.5)
Answer:
Solution to this example is given below
Point Q is 3 units right of the origin, and 2.5 units up It has x-coordinate 3 and y-coordinate 2.5, written (3, 2.5). It is located in Quadrant I.
Q = (3, 2.5) Final solution
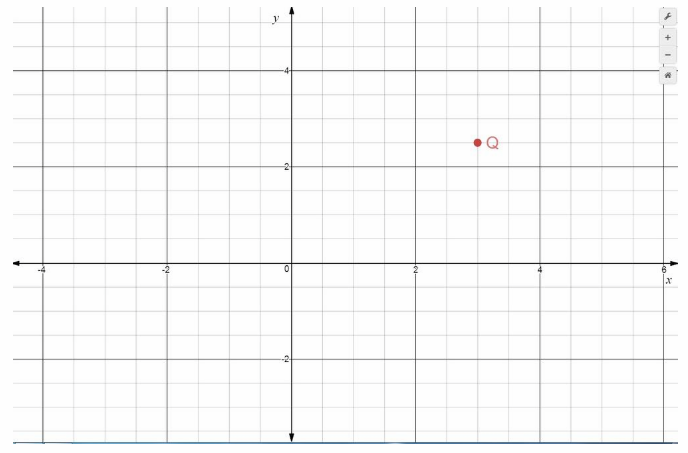
Q = (3, 2.5)
Question 8.
R(-4.5, -5)
Answer:
Solution to this example is given below. Point R is 4.5 units left of the origin, and 5 units down It has x-coordinate -4.5 and y-coordinate -5, written (-4.5, -5). It is located in Quadrant III
R = (-4.5, -5) Final solution
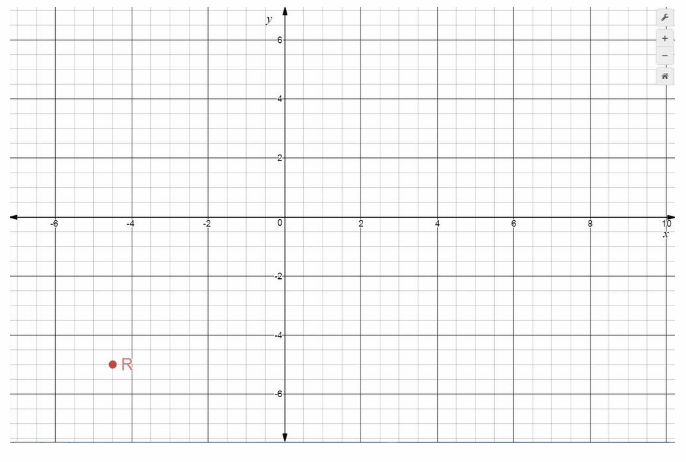
R(-4.5, -5)
Question 9.
S(4, -5)
Answer:
Solution to This example is given below. Point S is 4 units right of the origin, and 5 units down. It has x-coordinate 4 and y-coordinate -5, written (4, -5). It is located in Quadrant IV.
S = (4, -5) Final solution
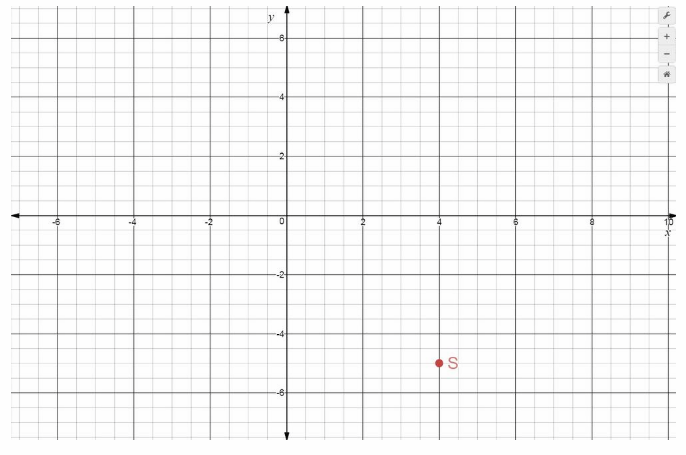
S(4, -5)
Question 10.
T(-2.5, 0)
Answer:
Solution to this example is given below.
Point T is 2.5 units left of the origin, and 0 units down/up. It has x-coordinate -2.5 and y-coordinate 0, written (-25, 0). It is located in Quadrant II.
T= (-2.5, 0) Final solution
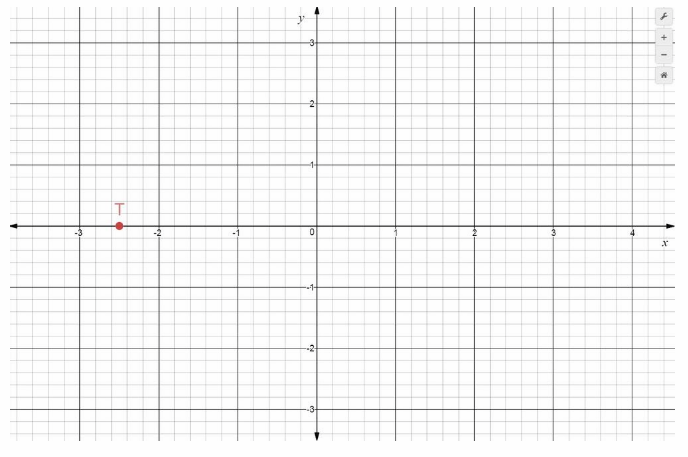
T(-2.5, 0)
Your Turn
Use the graph in the Example.
Question 11.
Ted lives 20 miles south and 20 miles west of the city represented on the graph in Example 3. His brother Ned lives 50 miles north of Ted’s house. Give the coordinates of each brother’s house.
Answer:
Ted lives 20 miles south and 20 miles west of the city represented on the graph, then the point of Teds location is given by (-20, -20). Note that the negative signs are chosen because of the given directions. If Ned’s house is 50 miles north of Ted, then add 50 to the y-coordinate of Teds location to determine Ned’s location, therefore (-20, -20 + 50) = (-20, 30).
Texas Go Math Grade 6 Lesson 14.1 Guided Practice Answer Key
Identify the coordinates of each point in the coordinate plane. Name the quadrant where each point is located. (Example 1)
Question 1.
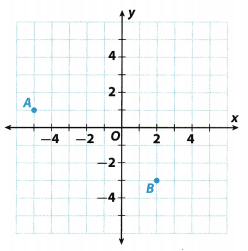
Point A is 5 units ____ of the origin and 1 unit ___ from the origin. Its coordinates are ___. It is in quadrant ___.
Answer:
Solution to this example is given below. Point A is 5 units Left of the origin, and 1 units up. It has x-coordinate -5 and y-coordinate 1, written (-5, 1). It is located in Quadrant II
A = (-5, 1) Final solution
A = (-5, 1)
Question 2.
Point B is ____ units right of the origin and ___ units down from the origin. Its coordinates are ____. It is in quadrant ____.
Answer:
Solution to this example is given below. Point B is 2 units right of the origin, and 3 units down. It has x-coordinate 2 and y-coordinate -3. written (2, -3). It is located in Quadrant IV
B = (2, -3) Final solution
B = (2, -3)
Graph and label each point on the coordinate plane above. (Example 2)
Question 3.
Point C at (-3.5, 3)
Answer:
Solution to this example is given below. Point C is 3.5 units left of the origin, and 3 units up. It has x-coordinate -3.5 and y-coordinate 3, written (-3.5, 3). It is located in Quadrant II.
C = (-3.5, 3) Final solution
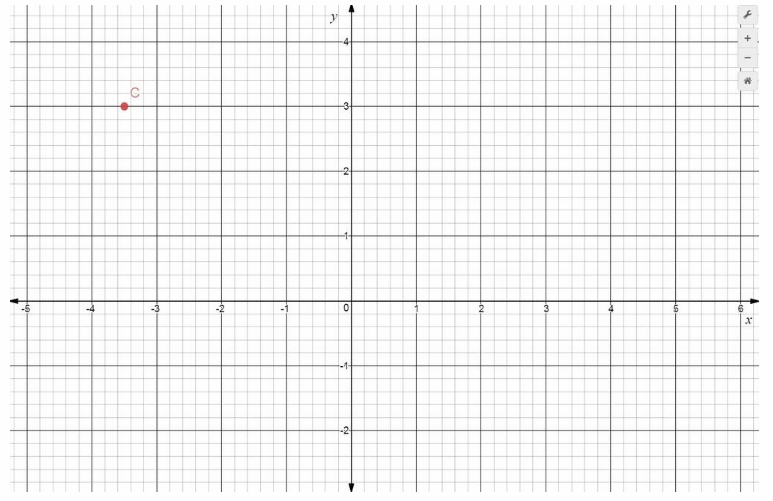
C(-3.5, 3)
Question 4.
Point D at (5, 0)
Answer:
Solution to this example is given below. Point D is 5 units right of the origin, and 0 units down/up It has x-coordinate 5 and y-coordinate 0, written (5, 0). It is located in Quadrant I.
D = (5, 0) Final solution
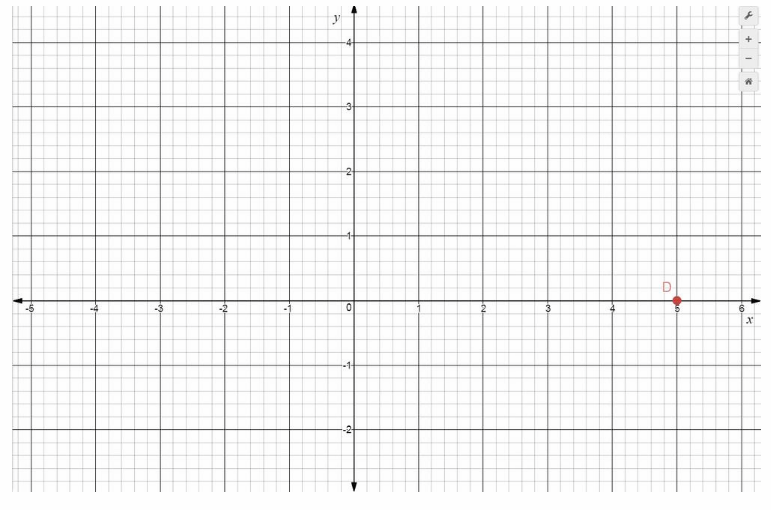
D(5, 0)
For 5-7, use the coordinate plane shown. (Example 3)
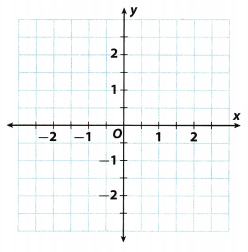
Question 5.
Describe the scale of the graph.
Answer:
Study the graph to determine the size represented by 1 grid. It can be seen that for both x and y-axes, 2 grids represent 1 unit so this means that each grid represents 0.5 units on each axes.
Question 6.
Plot point A at (-\(\frac{1}{2}\), 2).
Answer:
Solution to this example is given below
–\(\frac{1}{2}\) = -0.5 Convert to decimal number
Point A is 0.5 units left of the origin, and 2 units up. It has x-coordinate -0.5 and y-coordinate 2, written (-0.5, 2). It is located in Quadrant II.
A = (-0.5, 2) Final solution
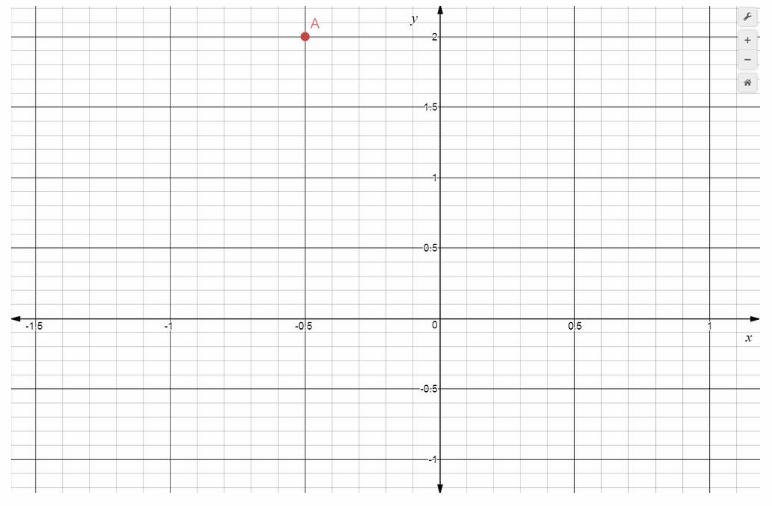
A = (0.5, 2)
Question 7.
Plot point 6 at (2\(\frac{1}{2}\), -2).
Answer:
Solution to this example is given below
2\(\frac{1}{2}\) = \(\frac{2 \times 2+1}{2}\) = 2.5 Convert to decimal number
Point B is 2.5 units right of the origin, and 2 units down. It has x-coordinate 2.5 and y-coordinate -2, written (2.5, -2). It is located in Quadrant IV.
B = (2.5, -2) Final solution
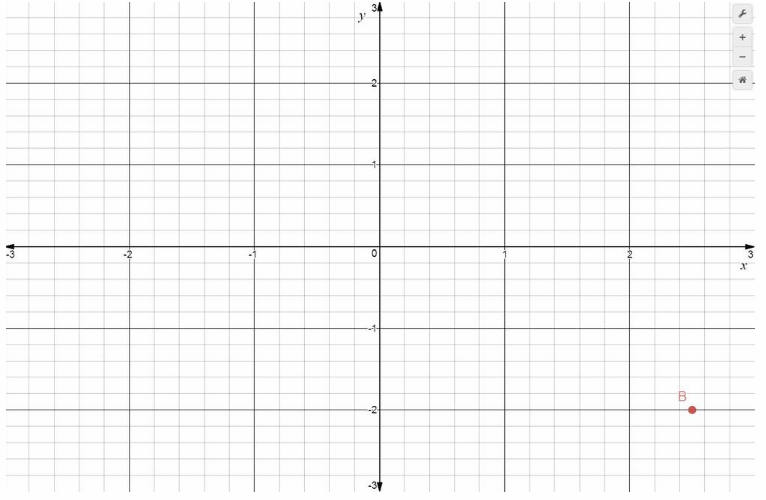
B = (2.5, -2)
Question 8.
Vocabulary Describe how an ordered pair represents a point on a coordinate plane. Include the terms x-coordinate, y-coordinate, and origin in your answer.
Answer:
The ordered pair represented by (x, y) = (a, b) means that the ordered pair is a units towards the right of the origin along the positive x-axis. If it is -a then the negative sign implies the left side of the origin on the negative x-axis. It also means that the ordered pair is b units above the origin along the positive y-axis. If it is -b then the negative sign implies along the negative y-axis.
Essential Question Check-In
Question 9.
Give the coordinates of a point that could be in each of the four quadrants, a point on the x-axis, and an point on the y-axis.
Answer:
Described point only could be point (0, 0) because it is the only point which is in each of the four quadrants.
Point (0, 0)
Texas Go Math Grade 6 Lesson 14.1 Independent Practice Answer Key
For 10-13, use the coordinate plane shown. Each unit represents 1 kilometer.
Question 10.
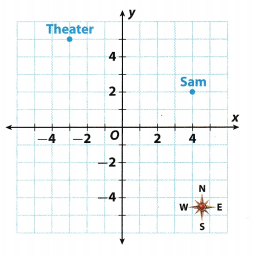
Write the ordered pairs that represent the location of Sam and the theater.
Answer:
Solution to this example is given below.
Sam is located 4 units right of the origin, and 2 units up. It has x-coordinate 4 and y-coordinate 4, written (4, 2). It is located in Quadrant I.
Theater is located 3 units left of the origin, and 5 units up. It has x-coordinate -3 and y-coordinate 5, written (-3, 5). It is located in Quadrant II.
Sam:(4 , 2): Theate(-3, 5) solution
Sam = (4, 2): Theater: (3, 5)
Question 11.
Describe Sam’s location relative to the theater.
Answer:
Evaluate the difference between the coordinates of Sam and the theater Therefore: 4 – (-3) = 7 and 2 – 5 = -3. This implies that Sam is 7 units on the right and 3 units south of the theater.
Question 12.
Sam wants to meet his friend Beth at a restaurant before they go to the theater. The restaurant is 9 km south of the theater. Plot and label a point representing the restaurant. What are the coordinates of the point?
Answer:
Solution to this example is given below
The restaurant is located 3 units left of the origin, and 4 units down. It has x-coordinate -3 and y-coordinate -4 written (-3, -4). It is located in Quadrant III.
Restaurant (-3, -4) Final solution
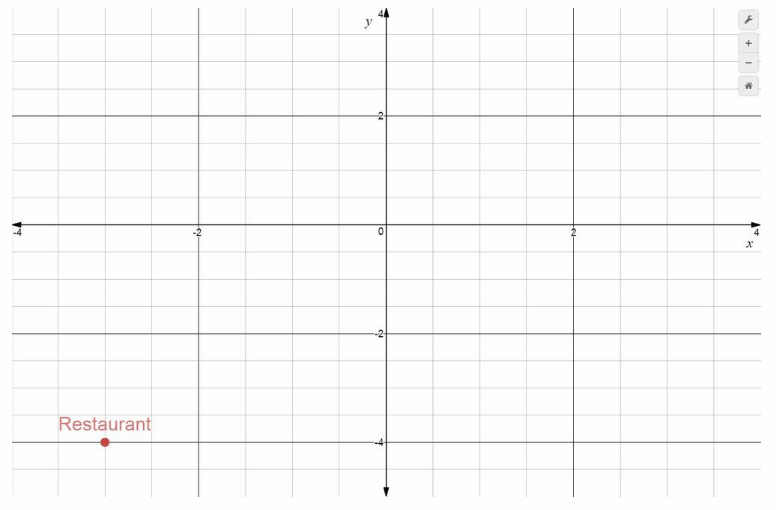
Restaurant ( -3, -4)
Question 13.
Beth describes her current location: “I’m directly south of the theater, halfway to the restaurant.” Plot and label a point representing Beth’s location. What are the coordinates of the point?
Answer:
Solution to this example is given below
Beth is located 3 units left of the origin, and 0.5 units up. It has x-coordinate -3 and y-coordinate 0.5, written (-3, 0.5) It is located in Quadrant II.
Beth (-3, 0.5) Final solution
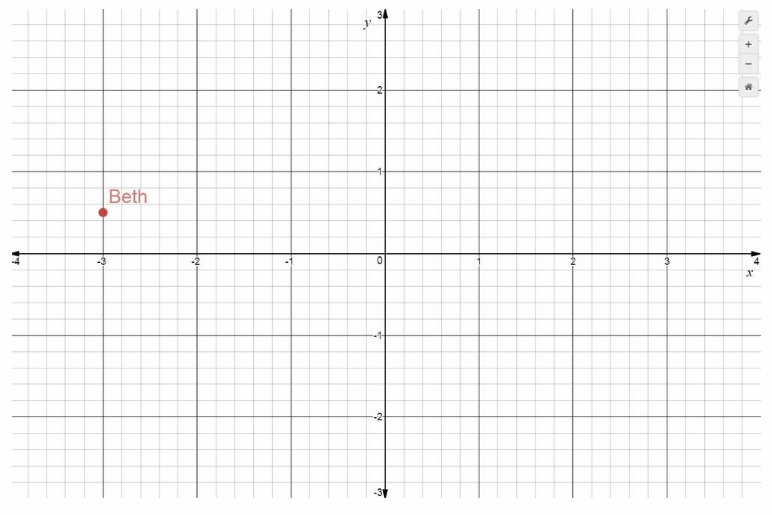
Beth (-3, 0.5)
For 14-15, use the coordinate plane shown.
Question 14.
Find the coordinates of points T, U, and V.
Answer:
Solution to this example is given below
Point T is 0.75 units right of the origin, and 1 units down. It has x-coordinate 0.75 and y-coordinate -1, written (0.75, -1). It is located in Quadrant IV.
Point U is 0.75 units right of the origin, and 1.25 units up. It has x-coordinate 0.75 and y-coordinate 1.25, written (0.75, 1.25) It is located in Quadrant I.
Point V is 0.75 units Left of the origin, and 1.25 units up. It has x-coordinate -0.75 and y-coordinate 1.25, written (-0.75, 1.25). It is located in Quadrant II.
T = (0.75, -1): U = (0.75, 1.25) : V = (-0.75, 1.25) Final solution
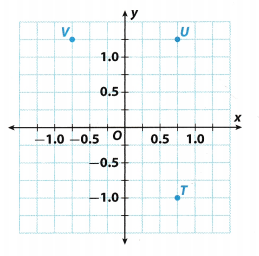
Question 15.
Points T, U, and V are the vertices of a rectangle. Point W is the fourth vertex. Plot point W and give its coordinates.
Answer:
Solution to this example is given below
Point W is 0.75 units left of the origin, and 1 units down. It has x-coordinate -015 and y-coordinate -1, written (-0.75, -1). It is located in Quadrant III.
w = (-0.75, -1) Final solution
Question 16.
Explain the Error Janine tells her friend that ordered pairs that have an x-coordinate of 0 lie on the x-axis. She uses the origin as an example. Describe Janine’s error. Use a counterexample to explain why Janine’s statement is false.
Answer:
A point lies on the x-axis when its y-coordinate is equal to 0, like the point (5, 0). The origin or (0, 0) represents the point where both x and y are 0. Another example is that of the point (0, 9). Its x-coordinate is equal to 0 but it does not lie on the x-axis but on the y-axis
Texas Go Math Grade 6 Lesson 14.1 H.O.T. Focus On Higher Order Thinking Answer Key
Question 17.
Critical Thinking Choose scales for the coordinate plane shown so that you can graph the points J(2, 40), K(3, 10), L(3, -40), M(-4, 50), and N(-5, -50). Explain why you chose the scale for each axis.
Answer:
Study the x-coordinates of the given points. The most negative one is -5 and the largest is 3, so 1 grid is equal to 1 unit on the x-axis.
Study the y-coordinates of the given points. The most negative one is -50 and the largest is 50, so 1 grid is equal to 10 units on the y-axis.
Question 18.
Communicate Mathematical Ideas Edgar wants to plot the ordered pair (1.8, -1.2) on a coordinate plane. On each axis, one grid square equals 0.1. Starting at the origin, how can Edgar find (1.8, -1.2)?
Answer:
1.8
Divide the coordinate by the scale to determine the number of grids to be moved across. Here \(\frac{1.8}{0.1}\) = 18 implies that from the origin, he will have to move 18 grids to the right and then \(\frac{1.2}{0.1}\) = 12 grids perpendicularly downwards to reach the point (1.8, -1.2).
Question 19.
Represent Real-World Problems Zach graphs some ordered pairs in the coordinate plane. The x-values of the ordered pairs represent the number of hours since noon, and the y-values represent the temperature at that time.
a. In which quadrants could Zach graph points? Explain your thinking.
Answer:
Zach’s points will lie either in the first quadrant if both the quantities are positive or in the fourth quadrant, if the temperature noted is negative.
b. In what part of the world and at what time of year might Zach collect data so that the points he plots are in Quadrant IV?
Answer:
He should note down these readings somewhere in Alaska in December to have all his points in the fourth quadrant.