Refer to our Texas Go Math Grade 6 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 6 Lesson 13.1 Answer Key Writing Inequalities.
Texas Go Math Grade 6 Lesson 13.1 Answer Key Writing Inequalities
Texas Go Math Grade 6 Lesson 13.1 Explore Activity Answer Key
Using inequalities to Describe Quantities
You can use inequality symbols with variables to describe quantities that can have many values.
A. The lowest temperature ever recorded in Florida was -2°F. Graph this temperature on the number line.
![]()
B. The temperatures 0°F, 3°F, 6°F, 5°F, and -1°F have also been recorded in Florida. Graph these temperatures on the number line.
C. How do the temperatures in B compare to -2? How can you see this relationship on the number line?
D. How many other numbers have the same relationship to -2 as the temperatures in B ? Give some examples.
E. Suppose you could graph all of the possible answers to D on a number line. What would the graph look like?
F. Let x represent all the possible answers to D.
Complete this inequality: x ________ – 2
Example 1
Graph the solutions of each inequality. Check the solutions.


Reflect
Question 1.
How is x < 5 different from x ≤ 5?
Answer:
x < 5 means that x can be any number less than 5 while x ≤ 5 means that x can be 5 and any number less than 5. The number 5 is a solution of x ≤ 5 but is not a solution of x < 5.
Your Turn
Question 2.
Graph the solution of the inequality t ≤ —4.
![]()
Answer:
Draw a solid circle at -4 to show that -4 is a solution.
Shade the number line to the left of -4 to show that numbers Less than -4 are solutions.
Check your solution.
Choose a number that is on the shaded section of the number line, such as -5. Substitute -5 for t.
-5≤ 4 : -5 Less than -4, so -5 is a solution
Graph the solution on a number line.

Example 2
A. Write an inequality that represents the phrase the sum of y and 2 is greater than 5. Draw a graph to represent the inequality.

B. To test the temperature rating of a coat, a scientist keeps the temperature below 5 °C. Write and graph an inequality to represent this situation.

Your Turn
Question 3.
Write an inequality that represents the phrase the sum of 1 and y is greater than or equal to 3. Check to see if y = 1 is a solution.
Answer:
Write and graph an inequality to represent each situation.
Question 4.
The highest temperature in February was 6°F. _________________
![]()
Answer:
Let t represent the temperature of a garter snake’s body during hibernation. Its temperature is greater than 3° C, so, required inequality is:
t > 3
Now, we will graph this situation.

Question 5.
Each package must weigh more than 2 ounces. _______________________

Answer:
Write the inequality. Let w represent the package.
w > 2 The package must weigh more than 2 ounces.
Graph the inequality.

Texas Go Math Grade 6 Lesson 13.1 Guided Practice Answer Key
Question 1.
Graph 1 ≤ x. Use the graph to determine which of these numbers are solutions of the inequality: -1, 3, 0, 1 (Explore Activity and Example 1)
![]()
Answer:
Graph of 1 ≤ x

It can be seen that the points -1 and 0 do not lie on the graph of 1 ≤ x so they are not the solutions of the given inequality. It can also be seen that the points 1 and 3 lie on the graph of 1 ≤ x so they are the solutions of the given inequality.
Question 2.
Graph -3 > z. Check the graph using substitution. (Example 1)
Answer:
Draw a solid circle at -3 to show that -3 is not a solution.
Shade the number line to the left of -3 to show that numbers less than -3 are solutions.
Check your answer.
Substitute -4 for z.
3 > – 4 : -3 ¡s greater than -4, so -4 is a solution
Graph the solution on a number line

Question 3.
Write an inequality that represents the phrase the sum of 4 and x is less than 6.” Draw a graph that represents the inequality, and check your solution. (Example 2)
Answer:
Write the inequality.
The sum of x and 4 is greater than 6
x + 4 > 6.
Graph the solution
For x + 4 to have a value greater than 6.
x must be a number greater than 2

Question 4.
During hibernation, a garter snake’s body temperature never goes below 3°C. Write and graph an inequality that represents this situation. (Example 2)
Answer:
Write the inequality. Let t represent the temperature in snake’s body.
t ≥ 3° F
The temperature must be is greater tan or equal to 3°
Graph the inequality.

Essential Question Check-In
Question 5.
Write an inequality to represent this situation: Nina wants to take at least $15 to the movies. How did you decide which inequality symbol to use?
Answer:
The words at least imply that the minimum amount Lina want to take to the movies is 815, so the inequality becomes: m ≥ 15. where m is money in dollars.
Texas Go Math Grade 6 Lesson 13.1 Independent Practice Answer Key
Question 6.
Which of the following numbers are solutions to x ≥ 0? -5, 0.03, -1, 0, 1.5, -6,
Answer:
The inequality x ≥ 0 implies that the solution will contain x and all numbers greater than 0, therefore 0, \(\frac{1}{2}\) and 1.5 are solutions of the given inequality. Note that these are all positive numbers.
Graph each inequality.
Question 7.
t ≤ 8
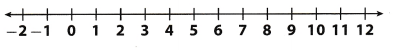
Answer:
Draw a solid circle at 8 to show that 8 is a solution
Shade the number line to the left of 8 to show that numbers less than 8 are solutions.
Check your solution.
Choose a number that is on the shaded section of the number line, such as 7. Substitute 7 for t.
7 ≤ 8 : 7 Less than 8, so 7 is a solution
Graph the solution on a number line.

Question 8.
-7 < h
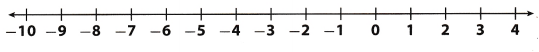
Answer:
Draw a solid circle at -7 to show that – 7 is not a solution.
Shade the number line to the right of -7 to show that numbers greater than -7 are solutions.
Check your answer.
Substitute -6 for 4.
-7 < -6 : -7 is less than -6, so -6 ¡s a solution
Graph the solution on a number line.

Question 9.
x ≥ -9
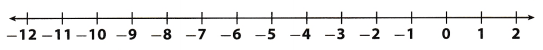
Answer:
Draw a solid circle at -9 to show that -9 is a solution.
Shade the number line to the right of -9 to show that numbers greater than -9 are solutions.
Check your solutions
Choose a number that is on the shaded section of the number line, such as -8. Substitute -8 for x.
-8 ≥ 9 : -8 greater than -9, so -8 is a solution
Graph the solution on a number line.

Question 10.
n > 2.5
![]()
Answer:
Draw a solid circle at 25 to show that 25 is not a solution.
Shade the number line to the right of 2.5 to show that numbers greater than 25 are solutions.
Check your answer.
Substitute 3 for n.
3 > 2.5 : 3 is greater than 2.5, so 3 is a solution
Graph the solution on a number line.

Question 11.
-4\(\frac{1}{2}\) > x
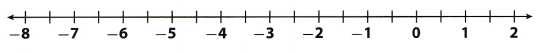
Answer:
-4\(\frac{1}{2}\) = \(-\frac{4 \times 2+1}{2}=-\frac{9}{2}\) = -4.5 Convert to decimal number
Draw a solid circle at-45 to show that -4.5 is not a solution.
Shade the number line to the left of -4.5 to show that numbers less than -4.5 are solutions.
Check your answer.
Substitute -5 for x.
-4.5 > 5 : -5 is less than -4.5, so -5 is a solution
Graph the solution on a number line.

Write an inequality that matches the number line model.
Question 12.
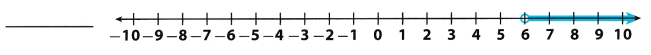
Answer:
Draw an empty circle at 6 to show that 6 is not a solution.
Shade the number line to the right of 6 to show that numbers greater than 6 are solutions.
Check your answer
Substitute 7 for x.
7 > 6: 7 greater than 6, so 7 is a solution
x > 6
Question 13.
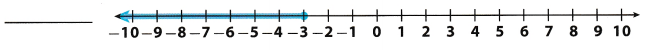
Answer:
Draw a solid circle at -3 to show that -3 is a solution.
Shade the number line to the left of -3 to show that numbers less than -3 are solutions.
Check your solution.
Choose a number that is on the shaded section of the number line, such as -4. Substitute -4 for x.
– 4 ≤ -3 : -4 less than -3, so -4 is a solution
x ≤ -3
Question 14.
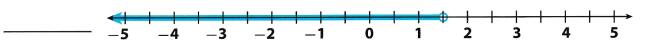
Answer:
Draw an empty circle at 1.5 to show that 1.5 is not a solution.
Shade the number line to the left of 1.5 to show that numbers less than 15 are solutions.
Check your answer.
Substitute 1 for x.
1 < 1.5 : 1 less than 1.5, so 1 is a solution
x < 1.5
Question 15.
![]()
Answer:
Draw a solid circle at -3.5 to show that -3.5 is a solution.
Shade the number Line to the right of -35 to show that numbers greater than -3.5 are solutions.
Check your solution.
Choose a number that is on the shaded section of the number line, such as -3. Substitute -3 for x.
-3 ≥ -3.5 : -3 greater than -3.5, so -3 is a solution
x ≥ -3.5
Question 16.
A child must be at least 48 inches tall to ride a roller coaster.
a. Write and graph an inequality to represent this situation.
![]()
Answer:
The word at least imp[y that the minimum height required for riding the roller coaster is 48 inches. The inequality to represent this situation is h ≥ 48, therefore its graph is:
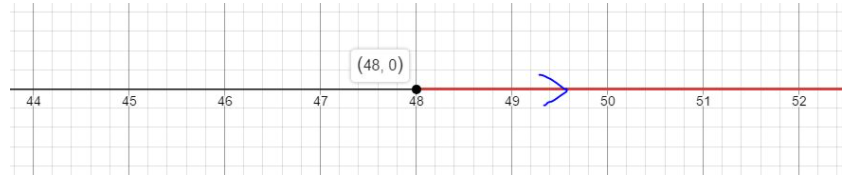
b. Can a child who is 46 inches tall ride the roller coaster? Explain.
Answer:
A child 46 inches tall will not be able to ride the roller coaster as the minimum height requirement is 48 inches. It can also be seen that the point 46 does not lie on the graph of the inequality.
Write and graph an inequality to represent each situation.
Question 17.
The stock is worth at least $ 14.50.
![]()
Answer:
Draw a solid circle at 14.5 to show that 145 is a solution.
Shade the number line to the right of 14.5 to show that numbers greater than 14.5 are solutions.
Check your solution.
Choose a number that is on the shaded section of the number line, such as 15. Substitute 15 for x.
15 ≥ 14.5 : 15 greater than 14.5, so 15 is a solution
Graph the solution on a number line.

Question 18.
The temperature is less than 3.5 °F.
![]()
Answer:
Write the inequality. Let t represent the temperature.
t < 3.5° F
The temperature must be less than 3.5°
Graph the inequality.

Question 19.
The goal of the fundraiser is to make more than $ 150.

Answer:
Draw a solid circle at 150 to show that 150 is not a solution.
Shade the number Line to the right of 150 to show that numbers greater than 150 are solutions.
Check your answer.
Substitute 200 for x.
200 > 150: 200 is greater than 150, so 200 is a solution
Graph the solution on a number line.

H.O.T. Focus on Higher Order Thinking
Question 20.
Communicate Mathematical Ideas Explain how to graph the inequality 8 ≥ y.
Answer:
The inequality 8 ≥ y is read as 8 is greater than or equal to y. This implies that the maximum value of y is 8 and than the inequality holds true for all values of y less than 8. The symbol: ≥ implies that there will be a closed dot on 8 and that 8 is the solution of the given inequality.
Therefore the graph of the given inequality will be:

Question 21.
Represent Real-World Problems The number line shows an inequality. Describe a real-world situation that the inequality could represent.

Answer:
Note that the open dot implies that the inequality can be represented by < or>.
The graph of the inequality shows values greater than 2.75 and an open dot on 2.75, this implies that the given graph can be represented by the inequality: x > 2.75.
Real world example: John is preparing for his exam and wants to spend more than 2.75 hours on his studies each day.
Question 22.
Critique Reasoning Natasha is trying to represent the following situation with a number line model: There are fewer than 5 students in the cafeteria. She has come up with two possible representations, shown below. Which is the better representation, and why?
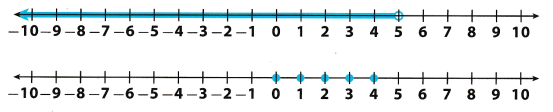
Answer:
The second model is a better representation of the given situation because of 2 reasons. The first reason is that the number of students in the cafeteria can never be less than 0, therefore all the negative values of students does not make sense in this context The second reason is that the number of students is discrete. What that means is that the number of student can never be 1.5, as this number has to be a whole number so decimal numbers do not make sense in this context.