Refer to our Texas Go Math Grade 6 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 6 Lesson 12.3 Answer Key Multiplication and Division Equations.
Texas Go Math Grade 6 Lesson 12.3 Answer Key Multiplication and Division Equations
Essential Question
How do you solve equations that contain multiplication or division?
Texas Go Math Grade 6 Lesson 12.3 Explore Activity Answer Key
Explore Activity
Modeling Equations
Deanna has a cookie recipe that requires 12 eggs to make 3 batches of cookies. How many eggs are needed per batch of cookies?
Let x represent the number of eggs needed per batch.

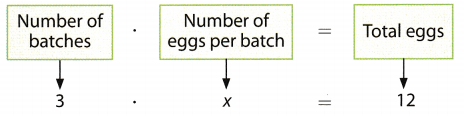
To answer this question, you can use algebra tiles to solve 3x = 12.
A. Model 3x = 12
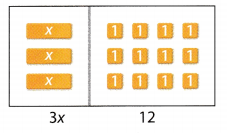
B. There are 3 x-tiles, so draw circles to separate the tiles into 3 equal groups. One group has been circled for you.
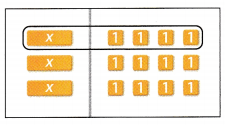
C. How many -hi-tiles are in each group? ____
This is the solution of the equation.
___ eggs are needed per batch of cookies.
Reflect
Question 1.
Look for a Pattern Why does it make sense to arrange the 12 tiles in 3 rows of 4 instead of any other arrangement of 12 + 1 -tiles, such as 2 rows of 6?
Answer:
The arrangement of tiles must be 3 rows because it is indicated in the problem that the eggs will be used in 3 batches of cookies.
The solution must indicate 3 batches of cookies which represent the 3 rows.
Your Turn
Solve the equation 3x = – 21. Graph the solution on a number line.
Question 2.
x = ______
Answer:
Determine the value of x
\(\frac{3 x}{3}\) = \(\frac{-21}{3}\) division property of equality
x = -7 value of x
Graph of the solution.

The value of the variable is -7.
Your Turn
Solve the equation \(\frac{y}{9}\) = -1. Graph the solution on a number line.
Question 3.
\(\frac{y}{9}\) = -1
y = ___
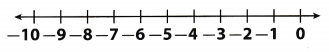
Answer:
Determine the vaLue of y.
9 • \(\frac{y}{9}\) = -1 • 9 multiply both sides of the equation by 9
y = -9 value of the variable y
Graph of the solution.
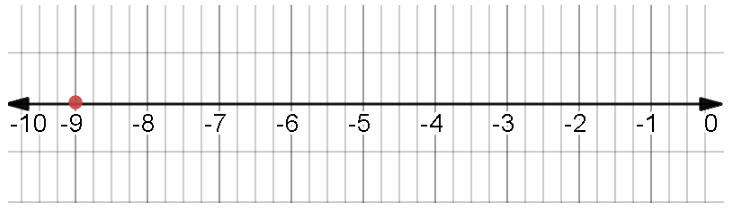
The value of the variable is -9.
Your Turn
Question 4.
Roberto is dividing his baseball cards equally among himself, his brother, and his 3 friends. Roberto was left with 9 cards. How many cards did Roberto give away? Write and solve an equation to solve the problem.
Answer:
Let the total number of cards be x and each person receives 9 so the equation becomes:
\(\frac{x}{5}\) = 9
Multiply both sides of the equation with 5 to isolate the variable on 1 side of the equation:
\(\frac{x}{5}\) × 5 = 9 × 5
Simplify to evaluate the variable:
x = 45
There were a total of 45 cards and he was left with 9, so he gave away 45 – 9 = 36.
he gave away 36 cards.
Your Turn
Question 5.
Write a real-world problem for the equation 11x = 385. Then solve the equation.
Answer:
Examine each part of the equation.
x is the unknown value you want to find.
11 is multiplied by x.
= 385 means that after multiplying 11 and x, the result is 385.
Use the equation to solve the problem.
11x = 385
\(\frac{11 x}{11}\) = \(\frac{385}{11}\) Divide both sides by 11
x = 35 Final solution
Texas Go Math Grade 6 Lesson 12.3 Guided Practice Answer Key
Question 1.
Caroline ran 15 miles in 5 days. She ran the same distance each day. Write and solve an equation to determine the number of miles she ran each day. (Explore Activity)
a. Let x represent the _____
Answer:
Variable
The variable x represents the number of miles ran each day.
b. 
Answer:
Equation
Representation

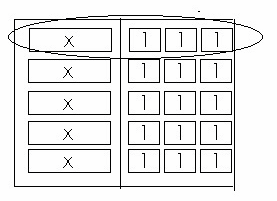
c. Draw algebra tiles to model the equation.
Caroline ran ___ miles each day.
Answer:
Algebra tiles
Based from the diagram, Caroline ran 3 miles each day.
Solve each equation. Graph the solution on a number line. (Examples 1 and 2)
Question 2.
x ÷ 3 = 3
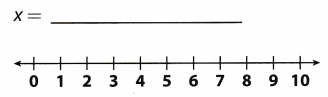
Answer:
Determine the value of x.
3 . \(\frac{x}{3}\) = 3 . 3 multiply both sides of the equation by 3
x = 9 value of the variabLe x
Graph of the solution.
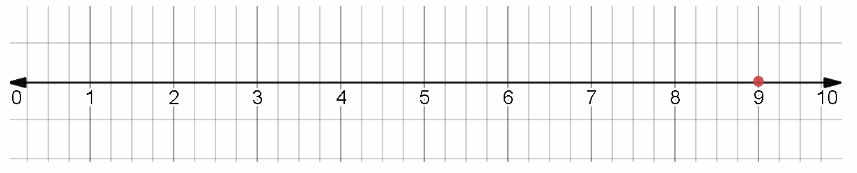
The value of the variable is 9.
Question 3.
4x = -32

Answer:
Determine the value of x
\(\frac{4 x}{4}\) = \(\frac{-32}{4}\) divide both sides of the equation by 4
x = -8 value of the variable x
Graph of the solution.
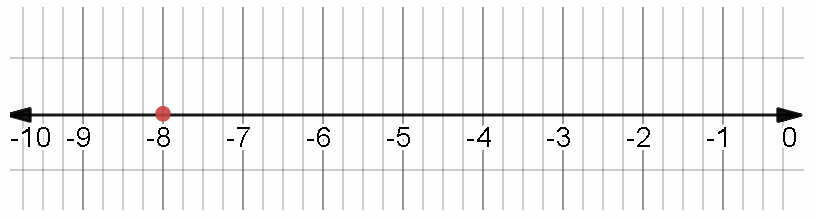
The value of the variable is 8.
Question 4.
The area of the rectangle shown is 24 square inches. How much longer is its length than its width? (Example 3)
Answer:
Area of a rectangle is the product of its length and width so the equation of area becomes:
6 × w = 24
Divide both sides of the equation with 6 to isolate the variable on 1 side of the equation:
\(\frac{6 w}{6}\) = \(\frac{24}{6}\)
Simplify to evaluate the variable:
w = 4
Therefore, the length is 6 – 4 = 2 inches longer than the width.
The length of this rectangle is 2 inches longer than its width.
Essential Question Check-in
Question 5.
How do you solve equations that contain multiplication or division?
Answer:
Case 1. If the coefficient associated with the variable on the variable side of the equation is being multiplied with it, then this coefficient is converted to 1 by dividing both sides of the equation with the same constant, to isolate the variable on 1 side of the equation. For example: 5x = 60 is solved by dividing both sides of the equation with 5, therefore the intermediate step becomes: \(\frac{5 x}{5}\) = \(\frac{60}{5}\) and the solution is x = 12.
Case 2. If the coefficient associated with the variable on the variable side of the equation is dividing it, then this coefficient is converted to 1 by multiplying both sides of the equation with the same constant, to isolate the
variable on 1 side of the equation. For example: \(\frac{x}{5}\) = 10 is solved by multiplying both sides of the equation with 5, therefore the intermediate step becomes: \(\frac{x}{5}\) × 5 = 10 × 5 and the solution is x = 50.
Texas Go Math Grade 6 Lesson 12.3 Independent Practice Answer Key
Write and solve an equation to answer each question.
Question 6.
Jorge baked cookies for his math class’s end-of-year party. There are 28 people in Jorge’s math class including Jorge and his teacher. Jorge baked enough cookies for everyone to get 3 cookies each. How many cookies did Jorge bake?
Answer:
Solution to this example is given below
\(\frac{x}{28}\) = 3 Notice that 28 is divided from x
\(\frac{x}{28}\) × 28 = 3 × 28 × 9 Multiply both sides of the equation by 28
x = 84 Simplify
Check; \(\frac{x}{28}\) = 3
\(\frac{84}{28}\) = 3 Substitute 84 for x
3 = 3 Divide on the left side.
x = 84 Final solution
Jorge baked 84 cookies
Question 7.
Sam divided a rectangle into 8 congruent rectangles that each have the area shown. What is the area of the rectangle before Sam divided it?
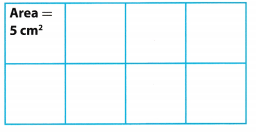
Answer:
Solution to this example is given below
\(\frac{x}{8}\) = 5 Notice that 8 is divided from x
\(\frac{x}{28}\) × 8 = 5 × 8 × 9 Multiply both sides of the equation by 8
x = 40 Simplify
Check; \(\frac{x}{8}\) = 5
\(\frac{40}{8}\) = 5 Substitute 40 for x
5 = 5 Divide on the Left side.
x = 40 Final solution
The area of the rectangle was 40 square centimeters.
x = 40
Question 8.
Carmen participated in a read-a-thon. Mr. Cole pledged $4.00 per book and gave Carmen $44. How many books did Carmen read?
Answer:
Examine each part of the equation.
x is the unknown value you want to find.
4 is multiplied by x.
44 means that after multiplying 4 and x, the result is 44.
Use the equation to solve the problem.
4x = 44
\(\frac{4 x}{4}\) = \(\frac{44}{4}\) Divide both sides by 4
x = 11 Final solution
Carmen read 11 books
x = 11
Question 9.
Lee drove 420 miles and used 15 gallons of gasoline. How many miles did Lee’s car travel per gallon of gasoline?
Answer:
Let the mpg of the car be x, then the equation of the total distance traveled is:
15x = 420
Step 2
Divide both sides of the equation with 15 to isolate the variable on 1 side of the equation:
\(\frac{15 x}{15}\) = \(\frac{420}{15}\)
Simplify to evaluate the variable:
x = 28
Lee’s car travelled 28 mites per gallon of gasoline.
Question 10.
On some days, Me’vin commutes 3.5 hours per day to the city for business meetings. Last week he commuted for a total of 14 hours. How many days did he commute to the city?
Answer:
Examine each part of the equation.
x is the unknown value you want to find.
3.5 is multiplied by x.
= 14 means that after multiplying 3.5 and x, the result is 14.
Use the equation to solve the problem.
3.5x = 14
\(\frac{3.5 x}{3.5}\) = \(\frac{14}{3.5}\) Divide both sides by 3.5
x = 4 Final solution
He commuted to the city on 4 days
x = 4
Question 11.
Dharmesh has a square garden with a perimeter of 132 feet. Is the area of the garden greater than 1,000 square feet?
Answer:
Perimeter of a square is the product of 4 and its side length s. Here the equation becomes:
4s = 132
Divide both sides of the equation with 4 to isolate the variable on 1 side of the equation:
\(\frac{4 s}{4}\) = \(\frac{132}{4}\)
Simplify to evaluate the variable:
s = 33
Area of a square is the square of its side length, therefore the equation becomes:
4 = 332 = 33 × 33
Evaluate:
A = 1089 > 1000
The area of the given square is greater than 1000 square feet.
Question 12.
Ingrid walked her dog and washed her car. The time she spent walking her dog was one-fourth the time it took her to wash her car. It took Ingrid 14 minutes to walk the dog. How long did it take Ingrid to wash her car?
Answer:
Let the total time spent in washing the car be x, then the equation for the time spent in walking the dog 5:
\(\frac{1}{4}\) × x = 14
Multiply both sides of the equation with 4 to isolate the variable on 1 side of the equation:
\(\frac{1}{4}\) × x × 4 = 14 × 4
Simplify to evaluate the variable:
x = 56
She took 56 minutes to wash her car.
Question 13.
Representing Real-World Problems Write and solve a problem involving money that can be solved with a multiplication equation.
Answer:
5 friends go out for a movie anti end up spending $50 on tickets. How much did each ticket cost?
Here the equation will he 5x = 50 and x = \(\frac{50}{5}\) = 10. Kach ticket costed $10.
Question 14.
Representing Real-World Problems Write and solve a problem involving money that can be solved with a division equation and has a solution of 1,350.
Answer:
Evaluate the total amount of funds raised a group of 5 friends if each one of them raised $270.
Let the total profit be x, then the equation for the profit of one person be is:
\(\frac{x}{5}\) = 270
Multiply both sides of the equation with 5 to isolate the variable on 1 side of the equation:
\(\frac{x}{5}\) × 5 = 5 × 270
Simplify to evaluate the variable:
x = 1350
Texas Go Math Grade 6 Lesson 12.3 H.O.T. Focus On Higher Order Thinking Answer Key
Question 15.
Communicate Mathematical Ideas Explain why 7 • \(\frac{x}{7}\) = x. How does this relate to solving division equations?
Answer:
If the given equation will be multiplied, it will be \(\frac{7 x}{7}\) and in simplified form will become x. It is related to solving division equation in order to isolate the variable to get its value on the other side of the equation.
It makes the variable isolated in one side of the equation.
Question 16.
Critical Thinking A number tripled and tripled again is 729. What is the number?
Answer:
SoLution to this example ¡s given below
3(3x) = 729
3(3x) = 729 Notice that 3x is multiplied to x
9x = 729 Simplify
\(\frac{9 x}{9}\) = \(\frac{729}{9}\) Divide both sides of the equation by 9
x = 81 Simplify
Check; 3(3x) = 729
3(3 × 81) = 729 Substitute 81 for x
729 = 729 Multiply on the left side.
x = 81 Final solution
The number is 81.
x = 81
Question 17.
Multistep Andre has 4 times as many model cars as Peter, and Peter has one-third as many model cars as Jade. Andre has 36 model cars.
a. Write and solve an equation to find how many model cars Peter has.
Answer:
Let the number of Peter’s cars be x, then the equation for the number of Andre’s cars 5:
4x = 36
Divide both sides of the equation with 4 to isolate the variable on 1 side of the equation:
\(\frac{4 x}{4}\) = \(\frac{36}{4}\)
Simplify to evaluate the variable:
x = 9
Peter has 9 cars.
b. Using your answer from part a, write and solve an equation to find how many model cars Jade has.
Answer:
Peter has 9 cars, then the equation for the number of Jades cars y 5:
\(\frac{y}{3}\) = 9
Multiply both sides of the equation with 3 to isolate the variable on 1 side of the equation:
\(\frac{y}{3}\) × 3 = 9 × 3
Simplify to evaluate the variable:
y = 27
Jade has 27 cars.