Texas Go Math Grade 6 Lesson 11.3 Answer Key Generating Equivalent Expressions

Refer to our Texas Go Math Grade 6 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 6 Lesson 11.3 Answer Key Generating Equivalent Expressions.

Texas Go Math Grade 6 Lesson 11.3 Answer Key Generating Equivalent Expressions

Essential Question
How can you identify and write equivalent expressions?

Texas Go Math Grade 6 Lesson 11.3 Explore Activity Answer Key

Explore Activity 1
Identifying Equivalent Expressions
One way to test whether two expressions might be equivalent is to evaluate them for the same value of the variable.

Match the expressions in List A with their equivalent expressions in List B.

A. Evaluate each of the expressions in the lists for x = 3.

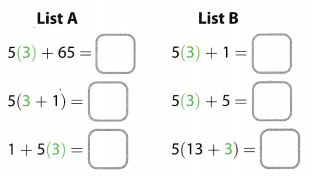
B. Which pair(s) of expressions have the same value for x = 3?

C. How could you further test whether the expressions in each pair are equivalent?

D. Do you think the expressions in each pair are equivalent? Why or why not?

Reflect

Question 1.
Error Analysis Lisa evaluated the expressions 2x and x² for x = 2 and found that both expressions were equal to 4. Lisa concluded that 2x and x2 are equivalent expressions. How could you show Lisa that she is incorrect?
Answer:
According to Lisas conclusion x² = 2x. If this was correct then this equation would have held true for all, values of x, but here this is not the case, as for x = 3, then 3² = 9 and 2(3) = 6 and 9 ≠ 6

Explore Activity 2
Modeling Equivalent Expressions
You can also use models to determine if two expressions are equivalent. Algebra tiles are one way to model expressions.

Determine if the expression 3(x + 2) is equivalent to 3x + 6.

A. Model each expression using algebra tiles.

B. The model for 3(x + 2) has ___ x tiles and ___ 1 tiles.
The model for 3x + 6 has ___ x tiles and ___ 1 tiles.
C. Is the expression 3(x + 2) equivalent to 3x + 6? Explain.

Reflect

Question 2.
Use algebra tiles to determine if 2(x – 3) is equivalent to 2x – 3. Explain your answer.
Answer:
Algebra tiles for the given expressions.

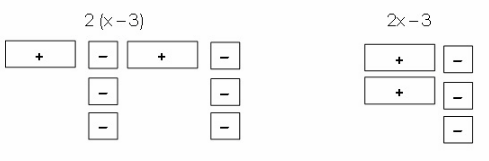
The parenthesis makes a difference in the given expressions. Parenthesis indicates grouping or multiplication which makes the expressions not equivalent
2 (x – 3) = 2x – 6 which is different from 2x – 3.
The expressions are not equivalent because the value of both expressions will not be similar.

Your Turn

For each expression, use a property to write an equivalent expression. Tell which property you used.

Question 3.
(ab)c = ____
Answer:
The operation in the expression is multiplication
You can use the Associative Property of Multiplication to write an equivalent expression:(ab)c = a(bc) (Final solution)
a(bc)

Question 4.
3y + 4y = _____
Answer:
Given expression:
3y + 4y = 4y + 3y
According to Commutative Property of Addition
3y + 4y = 4y + 3y. According to Commutative Property of Addition.

Your Turn

Use the properties of operations to determine if the expressions are equivalent.

Question 5.
6x – 8; 2(3x – 5)
Answer:
Given expression:
2(3x – 5)
Apply dstributive property to expand the parentheses
= 2(3x) + 2(-5)
Expand:
= 6x – 10x ≠ 6x – 8
6x – 10x ≠ 6x – 8

Question 6.
2 – 2 + 5x; 5x
Answer:
Determine if the expressions are equivalent
0 + 5x = 5x identity property of addition
5x = 5x
The expressions are equivalent because of identity property of addition.

Question 7.
Jamal bought 2 packs of stickers and 8 individual stickers. Use x to represent the number of stickers in a pack of stickers and write an expression to represent the number of stickers Jamal bought. Is the expression equivalent to 2(4 + x)? Check your answer with algebra tile models.
Answer:
There are x stickers in each pack and 2 packs are bought so the total number of stickers bought are x × 2 = 2x. He also bought 8 more stickers, so the total number of stickers bought are 2x + 8.
Expand the expression: 2(4 + x) = 8 + 2x = 2x + 8. Yes, the 2 expressions are equivalent.

Your Turn

Combine like terms.

Question 8.
8y – 3y = ___________
Answer:
Combine like terms
8y – 3y 8y and 3y are like terms
8y – 3y = y(8 – 3) Distributive Property
= y(5) Subtract inside the parentheses
= 5y Commutative Property of Multiplication
5y Final Solution

Question 9.
6x² + 4(x² – 1) = ______
Answer:
Given expression:
6x² + 4(x² – 1)
Apply distributive property to expand the parentheses:
= 6x² + 4x² – 4
Perform the indicated operation between like terms to combine like terms, therefore:
= 10x² – 4
6x² + 4(x² – 1)= 10x² – 4

Question 10.
4a⁵ – 2a⁵ + 4b + b = ___
Answer:
Given expression:
4a⁵ – 2a⁵ + 4b + b
Perform the indicated operation between like terms to combine like terms, therefore:
= 2a⁵ – 5b
4a⁵ – 2a⁵ + 4b + b = 2a⁵ + 5b

Question 11.
8m + 14 – 12 + 4n = ____
Answer:
Given expression:
8m + 14 – 12 + 4n
Perform the indicated operation between like terms to combine like terms, therefore:
= 8m – 2 – 4n
8m + 14 – 12 + 4n = 8m + 2 + 4n

Texas Go Math Grade 6 Lesson 11.3 Guided Practice Answer Key

Question 1.
Evaluate each of the expressions in the list for y 5. Then, draw lines to match the expressions in List A with their equivalent expressions in List B.

Answer:
Determine the equivalent expressions.


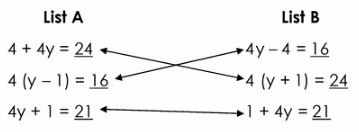
The equivalent expressions are:
a. 4 + 4y and 4 (y + 1) Distributive Property of Multiplication over Addition
b. 4 (y – 1) and 4y – 4 Distributive Property of Multiplication over Subtraction
c. 4y + 1 and 1 + 4y Commutative Property of Addition

Question 2.
Determine if the expressions are equivalent by comparing the models. (Explore Activity 2)

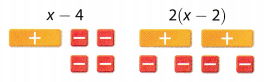
Answer:
The expressions are not equivalent based on the tiles shown. In x – 4, there are 1 tile for x and 4 tiles for -1 while in 2 (x – 2), there are 2 tiles for x and 4 tiles for -1.
x – 4 ≠ 2x – 4 by applying distributive property of multiplication over subtraction
The given expressions are not equivalent based on the models indicated.

For each expression, use a property to write an equivalent expression. Tell which property you used.

Question 3.
ab = ______________________
Answer:
Given expression:
ab = ba
According to commutative property of multiplication
ab = ba according to commutative property of multiplication.

Question 4.
5(3x – 2) = ___
Answer:
The operation in the expression is Multiplication.
You can use the Distributive Property to write an equivalent expression: 5(3x – 2) = 15x – 10 (Final solution)
15x – 10

Use the properties of operations to determine if each pair of expressions is equivalent. (Example 2)

Question 5.
\(\frac{1}{2}\)(4 – 2x); 2 – 2x ___________
Answer:
Given expression:
\(\frac{1}{2}\)(4 – 2x)
Apply distributive property of multiplication to expand the parentheses:
= \(\frac{1}{2}\)(4) + \(\frac{1}{2}\)(-2x)
Expand:
= 2 – x ≠ 2 – 2x
\(\frac{1}{2}\)(4 – 2x); ≠ 2 – 2x

Question 6.
\(\frac{1}{2}\)(6x – 2); 3 – x _____
Answer:
Given expression:
\(\frac{1}{2}\)(6x – 2)
Apply distributive property of multiplication to expand the parentheses:
= \(\frac{1}{2}\)(6x) + \(\frac{1}{2}\)(-2)
Expand:
= 3x – 1 ≠ 3 – x
\(\frac{1}{2}\)(6x – 2); 3 – x ≠ 3x – 1

Combine like terms. (Example 3)

Question 7.
32y + 12y _____________
Answer:
Combine like terms
32y + 12 32y and 12y are like terms.
32y + 12y = y(32 + 12) Distributive Property
= y(44) Add inside the parentheses.
= 44y Commutative Property of Multiplication
32y + 12y = 44y Final Solution
32y + 12y = 44y

Question 8.
12 + 3x – x – 12 = ___
Answer:
Combine like terms
12 + 3x – x – 12
12 + 3x – x – 12 = 2x Distributive Property
12 + 3x – x – 12 = 2x Final solution

Essential Question Check-In

Question 9.
Describe two ways to write equivalent algebraic expressions.
Answer:
The condensed form of an algebraic expression is by using parentheses, for example: 4(x + 3). Distributive property of multiplication can be applied here to expand it, therefore= 4x + 12. These 2 expressions are equal to each other.

Texas Go Math Grade 6 Lesson 11.3 Independent Practice Answer Key

For each expression, use a property to write an equivalent expression. Tell which property you used.

Question 10.
cd = ___
Answer:
Given expression:
cd = dc
According to commutative property of multiplication.
cd = dc according to commutative property of multiplication.

Question 11.
x + 13 = ___
Answer:
The operation in the expression is Addition.
You can use the Commutative Property of Addition to write an equivalent expression: x + 13 = 13 + x (Final solution)
13 + x

Question 12.
4(2x – 3) = ___
Answer:
Given expression:
4(2x – 3) = 8x – 12
According to distributive property of multiplication
4(2x – 3) = 8x – 12 according to distributive property of multiplication.

Question 13.
2 + (a + b) = ___
Answer:
The operation in the expression is Addition.
You can use the Associative Property of Addition to write an equivalent expression: 2 + (a + b) = (2 + a) + b (Final solution)
(2 + a) + b

Question 14.
Draw algebra tile models to prove that 4 + 8x and 4(2x + 1) are equivalent.
Answer:
Algebra tile models for the given expression.

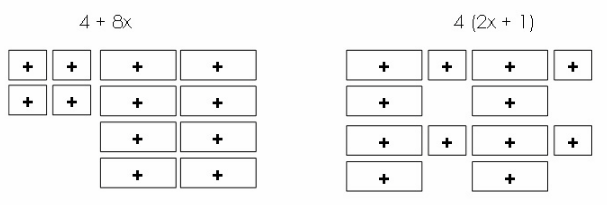
The expressions are equivalent as shown on the tiles. In 4 + 8, there are 4 tiles for +1 and 8 tiles for x which is similar to the tiles of 4(2x + 1).
The expressions are equivalent based on the diagram.

Combine like terms.

Question 15.
7x⁴ – 5x⁴ = ___________________
Answer:
7x⁴ – 5×4⁴ = x⁴(7 – 5) ← Distributive Property
= x⁴(2) ← Subtract inside the parentheses
= 2x⁴ ← Commutative Property of Multiplication
The final result is 2x⁴

Question 16.
32y + 5y = ________
Answer:
Given expression:
32y + 5y =
Perform the indicated operation between like terms to combine the like terms, therefore:
= 37y
32y + 5y = 37y

Question 17.
6b + 7b – 10 = ___
Answer:
Combine like terms
6b + 7b – 10 32y and 5y are like terms.
6b + 7b – 10 = 13b – 10 Distributive Property
13b – 10 Final Solution

Question 18.
2x + 3x + 4 = ___
Answer:
Combine like terms
2x + 3x + 4
2x + 3x + 4 = 5x + 4 Distributive Property
5x + 4 Final Solution

Question 19.
y + 4 + 3(y + 2) = ____
Answer:
Combine like terms
y + 4 + 3(y + 2)
y + 4 + 3(y + 2) = y + 4 + 3y + 6 Distributive Property
= y + 3y + 4 + 6 Commutative Property of Addition
= 4y + 10 Add
y + 4 + 3(y + 2) = 4y + 10
4y + 10 Final Solution

Question 20.
7a² – a² + 16 = ____
Answer:
Given expression:
7a² – a² + 16
Perform the indicated operation between like terms to combine the like terms, therefore:
= 6a² + 16
7a² – a² + 16 = 6a² + 16

Question 21.
3y² + 3(4y² – 2) = ____
Answer:
Given expression:
3y² + 3(4y² – 2)
Apply distributive property to expand the parentheses:
= 3y² + 12y² – 6
Perform the indicated operation between like terms to combine the like terms, therefore:
= 15y² – 6
3y² + 3(4y² – 2) = 15y² – 6

Question 22.
z² + z + 4z³ + 4z² = ___
Answer:
Combine like terms
z² + z + 4z³ + 4z²
z² + z + 4z³ + 4z² = 4z³ + 4z² + z² + z Comutative Property of Addition
= 4z³ + 5z² + z Distributive Property
z² + z + 4z³ + 4z² = 4z + 5z² + z
4z³ + 5z² + z Final Solution

Question 23.
0.5(x⁴ – 3) + 12 = ____
Answer:
Combine like terms
0.5(x⁴ – 3) + 12
0.5(x⁴ – 3) + 12 = 0.5x⁴ – 1.5 + 12 Distributive Property
= 0.5x⁴ + 10.5 Add
0.5(x⁴ – 3) + 12 = 0.5x⁴ + 10.5
0.5x⁴ + 10.5 Final Solution

Question 24.
\(\frac{1}{4}\)(16 + 4p) = ____
Answer:
Given expression:
\(\frac{1}{4}\)(16 + 4p)
Apply distributive property to expand the parentheses:
= \(\frac{1}{4}\)(16) + \(\frac{1}{4}\)(4p)
Expand:
= 4 + p
\(\frac{1}{4}\)(16 + 4p) = 4 + p

Question 25.
Justify Reasoning Is 3x + 12 – 2x equivalent to x + 12? Use two properties of operations to justify your answer.
Answer:
Determine if the expressions are equivalent.
= 3x – 2x + 12 commutative property of addition
= x + 12 combine like terms by subtracting the coefficient of the same variables
= 3 + 12 – 2x associative property of addition
= (3x – 2x) + 12 subtract the numbers inside the parenthesis
= x + 12

The given expressions are equivalent when commutative or associative property of addition is applied.

Question 26.
William earns $13 an hour working at a movie theater. Last week he worked h hours at the concession stand and three times as many hours at the ticket counter. Write and simplify an expression for the amount of money William earned last week.
Answer:
Last week he worked h hours at the concession stand and three times as many hours at the ticket counter This implies that he worked for 3 × h = 3h hours at the ticket counter The total number of hours worked are therefore: h + 3h = 4h.
His hourly rate at the theater is $13 so he earned $13 × 4h = $52h last week.

Question 27.
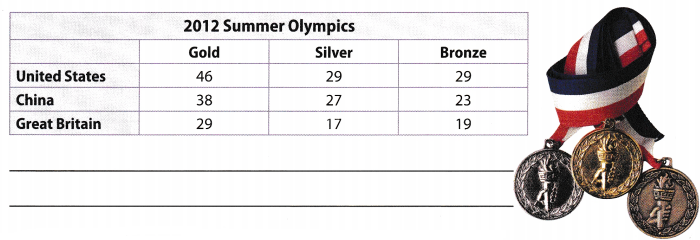
Multiple Representations Use the information in the table to write and simplify an expression to find the total weight of the medals won by the top medal-winning nations in the 2012 London Olympic Games. The three types of medals have different weights.

Answer:
Let g be the weight of a gold medal, s be the weight of a silver medal and b be the weight of a bronze medal.

The total weight of gold medals won by the 3 countries is g(46 + 38 + 29) = 113g. The total weight of silver medals won by the 3 countries is s(29 + 27 + 17) = 73s and the total weight of bronze medals won by the 3 countries is b(29 + 23 + 19) = 71b.
Their total sum is 113g + 73s + 71b.

Write an expression for the perimeters of each given figure. Simplify the expressions.

Question 28.
_____________

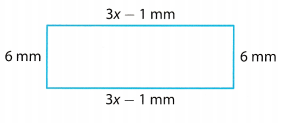
Answer:
Perimeter of a figure is the sum of its sides. Here 2 opposite sides are equal in length so the perimeter of the given figure is equal to 2(6) + 2(3x – 1):
Apply distributive property to expand the parentheses:
= 12 + 6x – 2
Perform the indicated operation between like terms to combine the like terms, therefore:
= 6x + 10
Perimeter of the figure shown is 6x + 10 millimeters.

Question 29.
___________

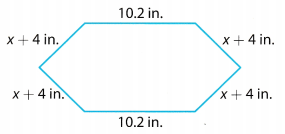
Answer:
Perimeter of a figure is the sum of its sides. Here 2 opposite sides are equal in Length and 4 other sides are also equal so the perimeter of the given figure is equal to 2(10.2) + 4(x + 4):

Apply distributive property to expand the parentheses:
= 20.4 + 4x + 16
Perform the indicated operation between like terms to combine the like terms, therefore:
= 4x + 36.4
Perimeter of the figure shown is 4x + 36.4 inches.

Texas Go Math Grade 6 Lesson 11.3 H.O.T. Focus On Higher Order Thinking Answer Key

Question 30.
Problem Solving Examine the algebra tile model.
a. Write two equivalent expressions for the model. ____

Answer:
The model shown represents 4 tiles of +1 and 6 tiles of -x. Therefore, the equivalent expressions for the model are 4 – 6x or 2 (2 – 3x).
The equivalent expressions are 4 – 6x and 2 (2 – 3)

b. What If? Suppose a third row of tiles identical to the ones above is added to the model. How does that change the two expressions?
Answer:
If a third row will be added, the expression will be 6 – 9x or 3 (2 – 3x). Since there will be 6 tiles of +1 and 9 tiles of -x.
The equivalent expressions are 6 – 9x and 3 (2 – 3x)

Question 31.
Communicate Mathematical Ideas Write an example of an expression that cannot be simplified, and explain how you know that it cannot be simplified.
Answer:
An example of such an expression is 8x + 100. It can be seen that the expression consists of 2 terms that are no like terms so the expression can no longer be simplified.

Question 32.
Problem Solving Write an expression that is equivalent to 8(2y + 4) that can be simplified.
Answer:
Given expression:
8(2y + 4)
Apply distributive property to expand the parentheses:
= 8(2y) + 8(4)
Simplify:
= 16y + 32
This expression can be broken down to form an expression with some like term that is equivalent to the given expression, therefore:
= 10y + 6y + 30 + 2
Note that there can be many answers to this question.