Refer to our Texas Go Math Grade 5 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 5 Lesson 7.1 Answer Key Factors and Divisibility.
Texas Go Math Grade 5 Lesson 7.1 Answer Key Factors and Divisibility
Unlock the Problem
Students in Carlo’s art class painted 32 square tiles for a mosaic. They will arrange the tiles to make a rectangle. Can the rectangle have 32 tiles arranged into 3 equal rows, without gaps or overlaps?

A composite number is a whole number greater than 1 that has more than two factors. You can use models and division to find factors of composite numbers.
Answer:
No, because 32 is not divisible by 3. There will be either be an excess of 2 tiles (3 by 10 rectangle) or a lack of 1 tile (3 by 11 rectangle)
One Way Draw a model.
Think: Try to arrange the tiles into 3 equal rows to make a rectangle.
A rectangle ___________ have 32 tiles arranged into 3 equal rows.
Answer:
Math Idea
A factor of a number divides the number evenly. This means the quotient is a whole number and the remainder is 0.
Another Way Use division.
If 3 is a factor of 32, then the unknown factor in 3 × ☐ = 32 is a whole number.

The unknown factor in 3 × ☐ = 32 a whole number.
So, a rectangle ___________ have 32 tiles arranged in 3 rows.
Answer:
Math Talk
Mathematical Processes
Explain how the model relates to the quotient and remainder for 32 ÷ 3.
Answer:
Divisibility Rules
A number is divisible by another number if the quotient is a counting number and the remainder is 0.
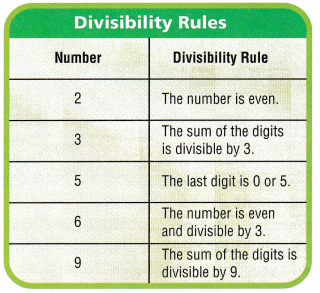
Some numbers have a divisibility rule. You can use a divisibility rule to tell whether one number is a factor of another.
Is 6 a factor of 72?
Think: If 72 is divisible by 6, then 6 is a factor of 72.
Test for divisibility by 6:
Is 72 even? _______
What is the sum of the digits of 72?
_______ + _______ = _______
Is the sum of the digits divisible by 3?
_______________________
72 is divisible by _______.
So, 6 is a factor of 72.
Answer:
If 72 is divisible by 6, then 6 is a factor of 72.
Test for divisibility by 6:
Is 72 even? Yes 72 is even.
What is the sum of the digits of 72?
7 + 2 = 9
Is the sum of the digits divisible by 3?
Yes the sum of digits is 9. So 9 is divisible by 3.
72 is divisible by 6.
So, 6 is a factor of 72.
Math Talk
Mathematical Processes
How are divisibility and factors related? Explain.
Answer:
Divisibility rules are a collection of general rules that we use to check if a given number is entirely divisible by another number.
Point out that “divisible by” means that when we divide one number by another, the result is a whole number. That is, a number ‘a’ is divisible by another number ‘b’ if the division a ÷ b is exact (no remainder). For example,
12 ÷ 4 = 3; therefore, 12 is divisible by 4.
Also, 12 is divisible by 3, because we can write the other division 12 ÷ 3 = 4. So, 12 is divisible by both 4 and 3. We can also say 4 and 3 are divisors or factors of 12.
A factor of a number divides the number evenly. This means the quotient is a whole number and the remainder is 0.
Share and Show
Question 1.
Is 4 a factor of 28? Draw a model to help.
Think: Can you make a rectangle with 28 squares in 4 equal rows?

4 ________ a factor of 28.
Answer:
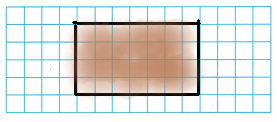
We can make a rectangle with 28 squares in 4 equal rows.
So, 4 is a factor of 28.
Explanation:
We can make a rectangle with 28 squares in 4 equal rows as we can observe in the above image. In the rectangle we can observe 4 rows and 7 columns with 28 squares. So, 4 is a factors of 28.
Is 5 a factor of the number? Write yes or no.
Question 2.
27
Answer:
No, 5 is not a factor of 27.
Explanation:
A factor of a number divides the number evenly. This means the quotient is a whole number and the remainder is 0. In this case the remainder is 2 and the quotient is not a whole number. So 5 is not a factor of 27.
Question 3.
30
Answer:
Yes, 5 is a factor of 30.
Explanation:
A factor of a number divides the number evenly. This means the quotient is a whole number and the remainder is 0. In this case the remainder is 0 and the quotient is 6. We know that 6 is a whole number. So 5 is a factor of 30.
Question 4.
36
Answer:
No, 5 is not a factor of 36.
Explanation:
A factor of a number divides the number evenly. This means the quotient is a whole number and the remainder is 0. In this case the remainder is 1 and the quotient not a whole number. So 5 is not a factor of 36.
Question 5.
53
Answer:
No, 5 is not a factor of 53.
Explanation:
A factor of a number divides the number evenly. This means the quotient is a whole number and the remainder is 0. In this case the remainder is 3 and the quotient is not a whole number. So 5 is not a factor of 53.
Problem Solving
List all the factor pairs in the table. Use a model or paper and pencil to help.
Question 6.
Answer:

The Factors of 24 are 1, 2, 3, 4, 6, 8, 12 and 24.
The factors of 24 in pairs are (1,24), (2,12) (3,8) and (4,6).
Explanation:
We can find the factors of number 24 , by multiplying two numbers in a pair to get the original number as 24, such as;
1 × 24 = 24
2 × 12 = 24
3 × 8 = 24
4 × 6 = 24
Question 7.
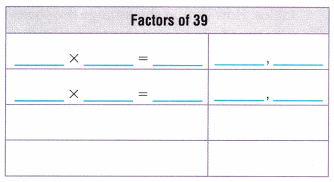
Answer:

The factors of 39 are: 1, 3, 13 and 39.
The factors of 39 in pairs are (1,39), (3, 13).
Explanation:
The factors of any number can be both positive and negative. To find the pair factors of 39, multiply the 2 numbers in a pair to have the original number as 39. Such numbers are as follows:
1 × 39 = 39; (1, 39)
3 × 13 = 39; (3, 13)
These are the positive pair factors for 39.
List all the factor pairs for the number. Make a table to help.
Question 8.
56
Answer:
Factor pairs of 56 are as below.
1 x 56 = 56 ⇒ (1, 56)
2 x 28 = 56 ⇒ (2, 28)
4 x 14 = 56 ⇒ (4, 14)
7 x 8 = 56 ⇒ (7, 8)
Explanation:
To find the pair factors, multiply the two numbers in a pair to get the original number as 56, such numbers are as follows. The pair factors of 56 are (1, 56), (2, 28), (4, 14) and (7, 8).
Question 9.
64
Answer:
Factor pairs of 64 are as below.
1 x 64 = 64 ⇒ (1, 64)
2 x 32 = 64 ⇒ (2, 32)
4 x 16 = 64 ⇒ (4, 16)
8 x 8 = 64 ⇒ (8, 8)
Explanation:
Factors are often written as pairs of numbers, which when multiplied together give the original number. Here, the required number is 64. The pair factors of 64 are (1, 64), (2, 32), (4, 16), (8, 8).
Question 10.
What’s the Error? George said if 2 and 4 are factors of a number, then 8 is a factor of the number, Is he correct? Explain.
Answer:
No, he is not correct.
Explanation:
I think George is not correct because 12 is a multiple of 2 and 4 but not 8.
Problem Solving
Use the table to solve 11-12.

Question 11.
Multi-Step Dirk bought a set of stamps. The number of stamps in the set he bought is divisible by 2, 3, 5, 6, and 9. Which set is it?
Answer:
The set is a Germany country with 90 stamps. 90 stamps he bought is divisible by 2, 3, 5, 6, and 9.
90 ÷ 2 = 45
90 ÷ 3 = 30
90 ÷ 5 = 18
90 ÷ 6 = 15
90 ÷ 9 = 10
Explanation:
In the above stamps sets table we can observe a country with number of stamps. The 90 stamps he bought are divisible by 2, 3, 5, 6, 9. So, the set is a Germany country with 90 stamps.
Question 12.
H.O.T. Multi-Step Gen wants to put 6 stamps on some pages in her stamp book and 9 stamps on other pages. Explain how she could do this with the stamp set for Sweden.

Answer:
Daily Assessment Task
Fill in the bubble completely to show your answer.
Question 13.
There are 54 people attending a party. Carla is arranging chairs and tables. How should she arrange the chairs so that there will be an equal number of people seated at each table?
(A) 12 chairs at each table
(B) 8 chairs at each table
(C) 9 chairs at each table
(D) 10 chairs at each table
Answer:

54 ÷ 9 = 6
She arranged 9 chairs. So that there will be an equal number of people seated at each table.
So, option C is correct.
Explanation:
There are 54 people attending a party. Carla is arranging chairs and tables. Divide 54 with 9 the result is 6. She arranged 9 chairs. So that there will be an equal number of people seated at each table. So, option C is correct.
Question 14.
Analyze Jake organizes 48 marbles into packs. He places the same number of marbles into each pack. How could he arrange the marbles?
(A) 8 or 10 in each pack
(B) 9 or 12 in each pack
(C) 10 or 12 in each pack
(D) 8 or 12 in each pack
Answer:

48 ÷ 8 = 6, 48 ÷ 12 = 4
Jack can place 8 marbles or 12 marbles in each pack.
So, option D is correct.
Explanation:
Jake organizes 48 marbles into packs. He places the same number of marbles into each pack. If we divide 48 by 8 then the result is 8. So, Jack can place 8 marbles in each pack. If we divide 48 by 12 then the result is 4. So, Jack can place 12 marbles in each pack. So, option D is correct.
Question 15.
Multi-Step Megan has 34 rocks in her rock collection. She wants to put 5 rocks in some cases and 7 rocks in other cases. How could she arrange the rocks?
(A) Have 6 cases of 5 rocks, and 1 case of 7 rocks.
(B) Have 4 cases of 5 rocks, and 2 cases of 7 rocks.
(C) Have 2 cases of 5 rocks, and 4 cases of 7 rocks.
(D) Have 5 cases of 5 rocks, and 2 cases of 7 rocks.
Answer:

If she put 5 rocks in 4 cases, and 7 rocks in 2 cases
5 x 4 + 7 x 2
20 + 14
34
So, option B is correct.
Explanation:
Megan has 34 rocks in her rock collection. She wants to put 5 rocks in some cases and 7 rocks in other cases. She arranged 5 rocks in 4 cases and 7 rocks in 2 cases. So, option B is correct.
Texas Test Prep
Question 16.
Mrs. Mastrioni bought a set of 80 stamps. She wanted to give all the stamps to her students as a reward. She could give equal numbers of stamps to
(A) 2 or 3 students.
(B) 2 or 6 students.
(C) 2, 4, 5, or 8 students.
(D) 2, 4, 8, or 9 students.
Answer:

80 ÷ 2 = 40
80 ÷ 4 = 20
80 ÷ 5 = 16
80 ÷ 8 = 10
She could give equal number of stamps to 2, 4, 5, or 8 students.
So, option C is correct.
Explanation:
Mrs. Mastrioni bought a set of 80 stamps. She wanted to give all the stamps to her students as a reward. She could give equal numbers of stamps to 2, 4, 5, or 8 students. So, option C is correct.
Texas Go Math Grade 5 Lesson 7.1 Homework and Practice Answer Key
List all the factor pairs in the table.
Question 1.
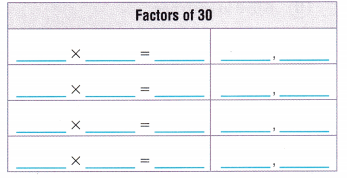
Answer:

The factors of 30 are 1, 2, 3, 5, 6, 10, 15, 30.
The pair factors of 30 are (1, 30), (2, 15), (3, 10) and (5, 6).
Explanation:
Factors of 30 are the numbers, which gives the result as 30 when multiplied together in pair of two. We can also say factors are the numbers that divide a number completely, leaving zero as a remainder. A pair of numbers, which are multiplied together resulting in an original number 30 is called the pair factors of 30. The pair factors of 30 are (1, 30), (2, 15), (3, 10) and (5, 6).
Question 2.
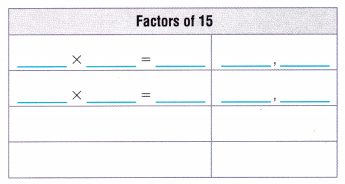
Answer:

The factors of 15 are: 1, 3, 5 and 15.
The factors of 15 in pairs are (1,15), (3, 5).
Explanation:
The factors of any number can be both positive and negative. To find the pair factors of 15, multiply the 2 numbers in a pair to have the original number as 15. Such numbers are as follows:
1 × 15 = 15; (1, 15)
3 × 5 = 15; (3, 5)
These are the positive pair factors for 15.
List all the factor pairs for the number. Make a table to help.
Question 3.
18
Answer:
The factor pairs of 18 are as below.
1 x 18 = 18 ⇒ (1, 18)
2 x 9 = 18 ⇒ (2, 9)
3 x 6 = 18 ⇒ (3, 6)
Explanation:
The numbers which are multiplied together give 18 are called pair factors of 18. The pair factor of 18 can be positive or negative. So, (1, 18), (2, 9) and (3, 6) are Positive Pair Factors of 18.
Question 4.
45
Answer:
The factor pairs of 45 are as below.
1 x 45 = 45 ⇒ (1, 45)
3 x 15 = 45 ⇒ (3, 15)
5 x 9 = 45 ⇒ (5, 9)
Explanation:
The numbers which are multiplied together give 45 are called pair factors of 45. The pair factor of 45 can be positive or negative. So, (1, 45), (3, 15) and (5, 9) are Positive Pair Factors of 45.
Question 5.
36
Answer:
The factor pairs of 36 are as below.
1 x 36 = 36 ⇒ (1, 36)
2 x 18 = 36 ⇒ (2, 18)
3 x 12= 36 ⇒ (3, 12)
4 x 9 = 36 ⇒ (4, 9)
6 x 6 = 36 ⇒ (6, 6)
Explanation:
The numbers which are multiplied together give 36 are called pair factors of 36. The pair factor of 36 can be positive or negative. So, (1, 36), (2, 18) and (3, 12), (4, 9), (6, 6) are Positive Pair Factors of 36.
Question 6.
63
Answer:
The factor pairs of 63 are as below.
1 x 63 = 63 ⇒ (1, 63)
3 x 21 = 63 ⇒ (3, 21)
7 x 9 = 63 ⇒ (7, 9)
Explanation:
The numbers which are multiplied together give 63 are called pair factors of 63. The pair factor of 63 can be positive or negative. So, (1, 63), (3, 21) and (7, 9), are Positive Pair Factors of 63.
Problem Solving
Question 7.
Planners for the city’s botanical garden are planting a rose garden. They want to plant 56 rose bushes. Can they arrange the rose bushes into 4 equal rows? Explain.
Answer:
56 ÷ 4 = 14
In one row they can plant 14 rose bushes.
Yes, they can arrange the 56 rose bushes into 4 equal rows.
Explanation:
Planners for the city’s botanical garden are planting a rose garden. They want to plant 56 rose bushes into 4 equal rows. Divide 56 by 4 the result is 14. So they can arrange 14 rose bushes in one row. So, in 4 equal rows they can arrange 56 rose bushes.
Question 8.
A marching band with 75 members makes two rectangular marching formations. One rectangle has 6 rows and the other rectangle has 9 rows. Explain how the members can form the two rectangles.
Answer:
One rectangle has 6 rows.
6 x 5 = 30
One rectangular marching have 30 members.
The other rectangle has 9 rows.
9 x 5 = 45
Other rectangular marching have 45 members.
Explanation:
A marching band with 75 members makes two rectangular marching formations. One rectangle has 6 rows. Multiply 6 rows with 5 columns the product is 30. One rectangular marching have 30 members. The other rectangle has 9 rows. Multiply 9 with 5 the product is 45. The other rectangular marching have 45 members.
Lesson Check
Fill In the bubble completely to show your answer.
Question 9.
Which number is divisible by 2, 3, and 6?
(A) 60
(B) 33
(C) 46
(D) 21
Answer:
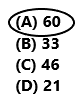
60 ÷ 2 = 30
60 ÷ 3 = 20
60 ÷ 6 = 10
So, option A is correct.
Explanation:
The number 60 is divisible by 2, 3 and 6. So, option A is correct.
Question 10.
Jo Beth organizes 63 party favors into gift bags. She places the same number of favors in each bag. How could she arrange the favors?
(A) 3 or 6 in each bag
(B) 6 or 9 in each bag
(C) 7 or 8 in each bag
(D) 7 or 9 in each bag
Answer:

63 ÷ 7 = 9
63 ÷ 9 = 7
She can arrange 7 favors in each bag or she can arrange 9 favors in each bag.
So, option D is correct.
Explanation:
Jo Beth organizes 63 party favors into gift bags. She places the same number of favors in each bag. She can arrange 7 favors in each bag or she can arrange 9 favors in each bag. So, option D is correct.
Question 11.
A package of marbles contains 20 blue marbles, 38 red marbles, 48 green marbles, and 16 yellow marbles. Which color of marbles can be divided evenly between 6 people?
(A) blue
(B) red
(C) green
(D) yellow
Answer:

Blue marbles:
20 ÷ 6 = 3.33
Red marbles:
38 ÷ 6 = 6.33
Green marbles:
48 ÷ 6 = 8
Yellow marbles:
16 ÷ 6 = 2.66
Green color marbles are divided evenly between 6 people.
So, option C is correct.
Explanation:
A package of marbles contains 20 blue marbles, 38 red marbles, 48 green marbles, and 16 yellow marbles. Divide 48 by 6 the result is 8. So, Green color marbles are divided evenly between 6 people. So, option C is correct.
Question 12.
The fifth-grade students participating In the math competition will be evenly divided into teams of 3 students each. How many students could be participating?
(A) 25
(B) 21
(C) 23
(D) 26
Answer:
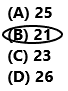
25 ÷ 3 = 8.33
21 ÷ 3 = 7
23 ÷ 3 = 7.66
26 ÷ 3 = 8.66
So, 21 students are participating in the math competition.
So, option B is correct.
Explanation:
The fifth-grade students participating in the math competition will be evenly divided into teams of 3 students each. Divide 21 by 3 the result is 7. So, option B is correct.
Question 13.
Multi-Step The librarian has 94 books to organize. He wants to put 5 books on some shelves and 6 books on other shelves. How could he arrange the books?
(A) Have 8 shelves of 5 books, and 9 shelves of 6 books.
(B) Have 9 shelves of 5 books, and 8 shelves of 6 books.
(C) Have 5 shelves of 6 books, and 6 shelves of 5 books.
(D) Have 7 shelves of 5 books, and 6 shelves of 6 books.
Answer:

He arranged the 5 books on 8 shelves and 6 books on 9 shelves.
5 x 8 + 6 x 9
40 + 54
94
So, option A is correct.
Explanation:
The librarian has 94 books to organize. He wants to put 5 books on some shelves. Multiply 5 with 8 the product is 40. He wants to put 6 books on other shelves. Multiply 6 with 9 the product is 54. Add 40 with 54 the sum is 94. He arranged the 5 books on 8 shelves and 6 books on 9 shelves. So, option A is correct.
Question 14.
Multi-Step A group of 72 students went on a field trip. The students traveled in vans, with an equal number of girls and boys in each van. If 42 boys went on the trip, how many vans were there?
(A) 9
(B) 8
(C) 7
(D) 6
Answer:
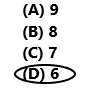
72 – 42 = 30
30 ÷ 6 = 5
There are 6 vans.
So, option D is correct.
Explanation:
A group of 72 students went on a field trip. The students traveled in vans, with an equal number of girls and boys in each van. If 42 boys went on the trip, then we have to subtract 42 from 72 the difference is 30. So, 30 girls went to the trip. So divide 30 by 6 the result is 5. So 6 vans are there with 5 boys and 5 girls in each van. So, option D is correct.