Refer to our Texas Go Math Grade 5 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 5 Lesson 2.7 Answer Key Adjust Quotients.
Texas Go Math Grade 5 Lesson 2.7 Answer Key Adjust Quotients
Unlock the Problem
A new music group makes 6,127 copies of its first CD. The group sells 75 copies of the CD at each of its shows. How many shows does it take the group to sell all of the CDs?
Divide. 6,127 ÷ 75 Estimate. 6,300 ÷ 70 = 90
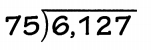
STEP 1: Use the estimate, 90. Try 9 tens.
A. Is the estimate too high, too low, or correct?
Answer:
We know that,
75 × 9 = 675
So,
612 < 675
Hence, from the above,
We can conclude that
The estimate is too high
B. Adjust the number in the quotient if needed.
Answer:
We know that,
75 × 8 = 600
So,
612 > 600
Hence, from the above,
We can conclude that
The quotient can be adjusted to 8
STEP 2: Estimate the next digit in the quotient. Divide the ones.
Estimate: 140 ÷ 70 = 2. Try 2 ones.
A. Is the estimate too high, too low, or correct?
Answer:
The remaining number in the given estimate is: 27
Now,
7 × 3 = 21
So,
21 is closer to 27 than 14
Hence, from the above,
We can conclude that
The estimate is too low
B. Adjust the number in the quotient if needed.
Answer:
We know that,
7 × 3 = 21
So,
27 > 21
Hence, from the above,
We can conclude that
The quotient can be adjusted to 3
So,
It takes the group about 83 shows to sell all of the CDs.
Try This! When the difference is equal to or greater than the divisor, the estimate is too low.
Divide. 336 ÷ 48 Estimate. 300 ÷ 50 = 6
Use the estimate. Try 6 ones.
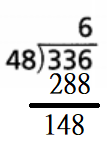
Since 288 is less than 336, the estimate is low.
336 ÷ 48 = 6
Adjust the estimated digit in the quotient, if needed. Then divide. Try
So,
336 ÷ 48 = 6
Math Talk
Mathematical Processes
Explain why using the closest estimate could be useful in solving a division problem.
Answer:
You can determine if an answer in the division is reasonable by learning to estimate the answers. Round the divisor to the nearest 10 or 100, depending on how many digits are in the divisor. Compare your estimate to the exact answer to determine if the exact answer is reasonable
Share and Show
Adjust the estimated digit in the quotient, if needed. Then divide.
Question 1.
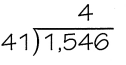
Answer:
The given division expression is: 1,546 ÷ 41
Now,
41 × 4 = 164
So,
154 < 164
So,
41 × 3 = 123
Hence, from the above,
We can conclude that
The adjusted estimated digit in the quotient is: 3
Question 2.
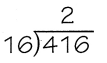
Answer:
The given division expression is: 416 ÷ 16
Now,
16 × 2 = 32
So,
41 > 32
Hence, from the above,
We can conclude that
The adjusted estimated digit in the quotient is: 2
Question 3.
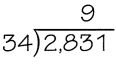
Answer:
The given division expression is: 2,831 ÷ 34
Now,
34 × 9 = 306
So,
283 < 306
So,
34 × 8 = 272
Hence, from the above,
We can conclude that
The adjusted estimated digit in the quotient is: 8
Problem Solving
H.O.T. Algebra Write the unknown number for each ☐.
Question 4.
☐ ÷ 33 = 11
☐ = ________
Answer:
Let the missing digit be: x
So,
The given expression is:
x ÷ 33 = 11
Now,
Multiply with 33 on both sides
So,
x = 11 × 33
x = 363
Hence, from the above,
We can conclude that
The missing digit in the given expression is: 363
Question 5.
1,092 ÷ 52 = ☐
☐ = _________
Answer:
Let the missing digit be: x
So,
The given expression is:
1,092 ÷ 52 = x
So,
x = 21
Hence, from the above,
We can conclude that
The missing digit in the given expression is: 21
Question 6.
429 ÷ ☐ = 33
☐ = ___________
Answer:
Let the missing digit be: x
So,
The given expression is:
429 ÷ x = 33
Now,
Divide by 33 into both sides
So,
x = \(\frac{429}{33}\)
x = 13
Hence, from the above,
We can conclude that
The missing digit in the given expression is: 13
Question 7.
How do you know whether an estimated quotient is too low or too high? Explain.
Answer:
If the multiplication of divisor and quotient is greater than the dividend, then the estimate is too high
If the multiplication of divisor and quotient is less than the dividend, then the estimate is too low
Unlock the Problem
Question 8.
Multi-Step A banquet hall serves 2,394 pounds of turkey during a 3-week period. If the same amount is served each day, how many pounds of turkey does the banquet hall serve each day?
(A) 50,274 pounds
(B) 798 pounds
(C) 342 pounds
(D) 114 pounds
a. What do you need to find?
Answer:
It is given that
A banquet hall serves 2,394 pounds of turkey during a 3-week period. If the same amount is served each day
Hence,
The information that you need to find is the number of pounds of turkey does the banquet hall serve each day
b. What information are you given?
Answer:
The given information is:
A banquet hall serves 2,394 pounds of turkey during a 3-week period. If the same amount is served each day
c. What other information will you use?
Answer:
We know that,
1 week = 7 days
So,
3 weeks = 3 × 7
= 21 days
Hence, from the above,
We can conclude that
The other information you will use is the number of days present in a 3-week period
d. Find how many days there are in 3 weeks.
There are ________ days in 3 weeks.
Answer:
We know that,
1 week = 7 days
So,
3 weeks = 3 × 7
= 21 days
Hence, from the above,
We can conclude that
There are 21 days in 3 weeks
e. Divide to solve the problem.
Answer:
It is given that
A banquet hall serves 2,394 pounds of turkey during a 3-week period. If the same amount is served each day
So,
According to the given information,
The number of pounds of turkey does the banquet hall serve each day = \(\frac{2,394}{21}\)
Now,
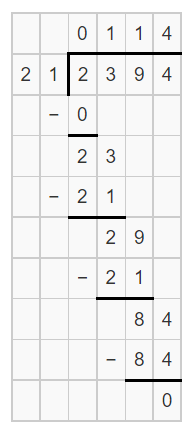
Hence, from the above,
We can conclude that
The number of pounds of turkey does the banquet hall serve each day is: 114 pounds
f. Fill in the bubble for the correct answer choice.
Answer:
The bubble for the correct answer choice is:

Question 9.
H.O.T. Multi-Step Kainoa collects trading cards. He has 1,025 baseball cards, 713 basketball cards, and 836 football cards. He wants to put all of them in albums. Each page in the album holds 18 cards. How many pages will he need to hold all of his cards?

Answer:
It is given that
Kainoa collects trading cards. He has 1,025 baseball cards, 713 basketball cards, and 836 football cards. He wants to put all of them in albums. Each page in the album holds 18 cards.
Now,
The total number of cards Kainoa collected = 1,025 + 713 + 836
= 2,574 cards
So,
According to the given information,
The number of pages will Kainoa need to hold all of his cards = \(\frac{2,574}{18}\)
= 143 pages
Hence, from the above,
We can conclude that
The number of pages will Kainoa need to hold all of his cards is: 143 pages
Question 10.
The Box Sox company packs 12 pairs of socks in a box. How many boxes will the company need to pack 1,020 pairs of socks?
Answer:
It is given that
The Box of Sox company packs 12 pairs of socks in a box
So,
According to the given information,
The number of boxes will the company needed to pack 1,020 pairs of socks = \(\frac{1,020}{12}\)
= 85 boxes
Hence, from the above,
We can conclude that
The number of boxes will the company needed to pack 1,020 pairs of socks is: 85 boxes
Daily Assessment Task
Fill in the bubble completely to show your answer.
Question 11.
Apply A ranch director would like to place a fence around some land he purchased for horses. He needs 992 feet of wire to fence the area. There are 45 feet of fence in each roll. How many rolls should he buy?
(A) 25 rolls
(B) 22 rolls
(C) 23 rolls
(D) 20 rolls
Answer:
It is given that
A ranch director would like to place a fence around some land he purchased for horses. He needs 992 feet of wire to fence the area. There are 45 feet of fence in each roll
So,
According to the given information,
The number of rolls the ranch director should buy = \(\frac{992}{45}\)
= 22 rolls
Hence, from the above,
We can conclude that
The number of rolls the ranch director should buy is:

Question 12.
Sarah works part-time at a zoo. She purchases food for the lions. The lions eat 1,330 pounds of food a year. The food comes in 22-pound bags. Which shows the closest estimate of how many bags of food Sarah orders each year?
(A) 1,000 ÷ 20 = 50
(B) 1,300 ÷ 20 = 65
(C) 1,200 ÷ 30 = 40
(D) 1,400 ÷ 20 = 70
Answer:
It is given that
Sarah works part-time at a zoo. She purchases food for the lions. The lions eat 1,330 pounds of food a year. The food comes in 22-pound bags
Now,
The number of bags of food Sarah orders each year = 1,330 ÷ 22
Now,
Estimate:
The number of bags of food Sarah orders each year = 1,300 ÷ 20
Hence, from the above,
We can conclude that
The closest estimate of how many bags of food Sarah orders each year is:

Question 13.
Multi-Step Dylan traveled through Texas for the summer. He took 15 photos each day for 18 days. He placed the photos in a 30-page album. If each page has the same number of photos, how many photos are on each page?
(A) 8
(B) 12
(C) 9
(D) 15
Answer:
It is given that
Dylan traveled through Texas for the summer. He took 15 photos each day for 18 days. He placed the photos in a 30-page album.
So,
According to the given information,
The number of photos present on each page = \(\frac{15 × 18}{30}\)
= 9 photos
Hence, from the above,
We can conclude that
The number of photos present on each page is:
Texas Test Prep
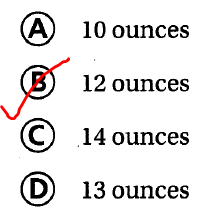
Question 14.
Marcos mixes 624 ounces of lemonade. He wants to fill the 52 cups he has with equal amounts of lemonade. How much lemonade should he put in each cup?
(A) 10 ounces
(B) 12 ounces
(C) 14 ounces
(D) 13 ounces
Answer:
It is given that
Marcos mixes 624 ounces of lemonade. He wants to fill the 52 cups he has with equal amounts of lemonade
So,
According to the given information,
The number of lemonades Marcos should put in each cup = \(\frac{624}{52}\)
= 12 ounces
Hence, from the above,
We can conclude that
The number of lemonades Marcos should put in each cup is:
Texas Go Math Grade 5 Lesson 2.7 Homework and Practice Answer Key
Divide.
Question 1.
3,234 ÷ 32
Answer:
The given division expression is: 3,234 ÷ 32
Now,
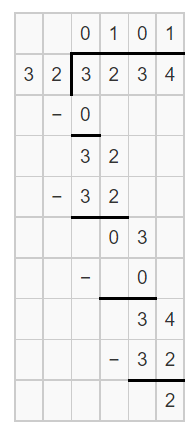
Hence, from the above,
We can conclude that
3,234 ÷ 32 = 101 R 2
Question 2.
1,453 ÷ 16
Answer:
The given division expression is: 1,453 ÷ 16
Now,
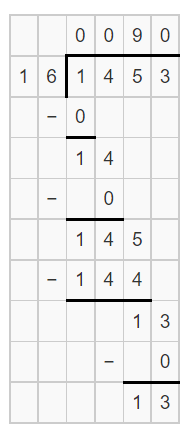
Hence, from the above,
We can conclude that
1,453 ÷ 16 = 90 R 13
Question 3.
6,305 ÷ 42
Answer:
The given division expression is: 6,305 ÷ 42
Now,

Hence, from the above,
We can conclude that
6,305 ÷ 42 = 150 R 5
Question 4.
1,074 ÷ 21
Answer:
The given division expression is: 1,074 ÷ 21
Now,
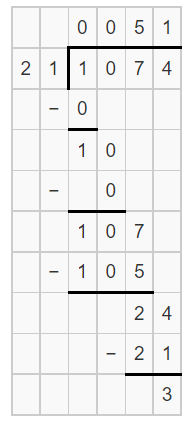
Hence, from the above,
We can conclude that
1,074 ÷ 21 = 51 R 3
Question 5.
4,893 ÷ 28
Answer:
The given division expression is: 4,893 ÷ 28
Now,
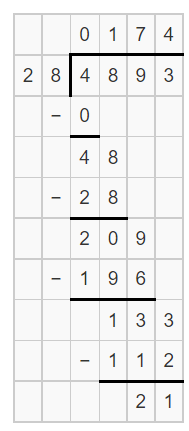
Hence, from the above,
We can conclude that
4,893 ÷ 28 = 174 R 21
Question 6.
2,015 ÷ 15
Answer:
The given division expression is: 2,015 ÷ 15
Now,

Hence, from the above,
We can conclude that
2,015 ÷ 15 = 134 R 5
Write the unknown number for each ☐.
Question 7.
☐ ÷ 75 = 23
☐ = __________
Answer:
Let the missing number be: x
Now,
The given expression is:
x ÷ 75 = 23
Now,
Multiply with 75 on both sides
So,
x = 23 × 75
Now,
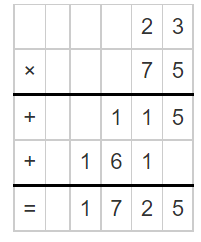
Hence, from the above,
We can conclude that
The missing number in the given expression is: 1,725
Question 8.
658 ÷ 47 = ☐
☐ = ___________
Answer:
Let the missing number be: x
Now,
The given expression is:
658 ÷ 47 = x
Now,
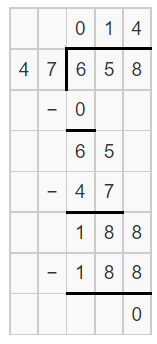
Hence, from the above,
We can conclude that
The missing number in the given expression is: 14
Question 9.
3,360 ÷ ☐ = 80
☐ = ____________
Answer:
Let the missing number be: x
Now,
The given expression is:
3,360 ÷ x = 80
Now,
x = 3,360 ÷ 80
Now,
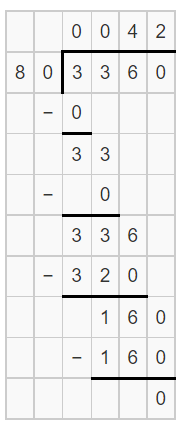
Hence, from the above,
We can conclude that
The missing number in the given expression is: 42
Problem Solving
Question 10.
Kirsten wants to divide 762 ÷ 21. She estimates that 2 is the first digit in the quotient. Is her estimate correct? Explain.
Answer:
It is given that
Kirsten wants to divide 762 ÷ 21. She estimates that 2 is the first digit in the quotient
Now,
By using the Long Division,
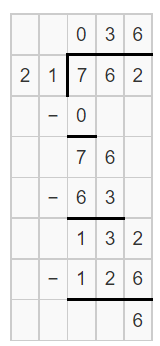
Now,
From the above division,
We can observe that
The first digit in the quotient is: 3
Hence, from the above,
We can conclude that
The estimate of Kirsten is not correct
Question 11.
Ming has 4,173 songs on his MP3 player. He organizes the songs into 39 playlists with the same number of songs in each list. How many songs are in each playlist?
Answer:
It is given that
Ming has 4,173 songs on his MP3 player. He organizes the songs into 39 playlists with the same number of songs in each list
So,
According to the given information,
The number of songs present in each playlist = 4,173 ÷ 39
Now,
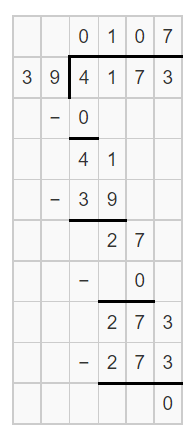
Hence, from the above,
We can conclude that
The number of songs present in each playlist is: 107 songs
Lesson Check
Fill in the bubble completely to show your answer.
Question 12.
Mr. Longo bakes 573 muffins to be sold at the school football game. He puts the muffins into boxes of 15. What is the greatest number of full boxes Mr. Longo will bring to the game?
(A) 35
(B) 38
(C) 41
(D) 39
Answer:
It is given that
Mr. Longo bakes 573 muffins to be sold at the school football game. He puts the muffins into boxes of 15
Now,
According to the given information,
The greatest number of full boxes Mr. Longo will bring to the game = 573 ÷15
Now,
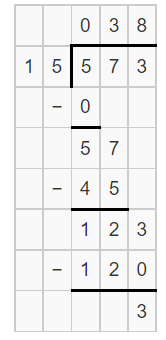
Hence, from the above,
We can conclude that
The greatest number of full boxes Mr. Longo will bring to the game is:
Question 13.
Multi-Step A movie theater sold 4,494 tickets during a two-week period. If the same number of tickets were sold each day, how many tickets were sold on Wednesday and Thursday of one week?
(A) 600
(B) 642
(C) 321
(D) 806
Answer:
It is given that
A movie theater sold 4,494 tickets during a two-week period and the same number of tickets were sold each day
Now,
We know that,
1 week = 7 days
So,
2 weeks = 14 days
So,
The number of tickets sold on each day = 4,494 ÷ 14
Now,
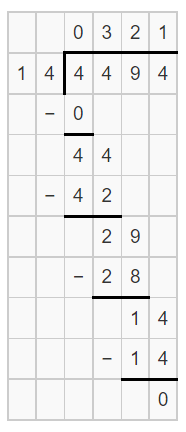
So,
The number of tickets sold on Wednesday and Thursday of one week = 2 × 321
= 642 tickets
Hence, from the above,
We can conclude that
The number of tickets sold on Wednesday and Thursday of one week is:

Question 14.
Jenny wants to estimate the quotient for 6,253 ÷ 39. Which is the best estimate for the first digit in the quotient?
(A) 1
(B) 2
(C) 4
(D) 3
Answer:
It is given that
Jenny wants to estimate the quotient for 6,253 ÷ 39
Now,
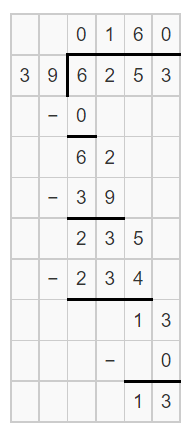
Hence, from the above,
We can conclude that
The best estimate for the first digit in the quotient is:
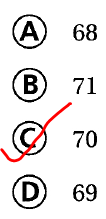
Question 15.
An art museum has 1,120 paintings. To display the paintings, the curator will divide the paintings equally among 16 rooms. How many paintings will be displayed in each room?
(A) 68
(B) 71
(C) 70
(D) 69
Answer:
It is given that
An art museum has 1,120 paintings. To display the paintings, the curator will divide the paintings equally among 16 rooms
Now,
According to the given information,
The number of paintings that will be displayed in each room = 1,120 ÷ 16
Now,
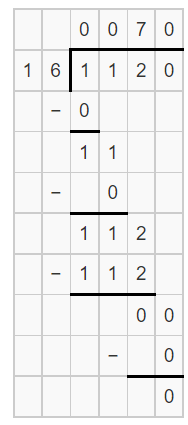
Hence, from the above,
We can conclude that
The number of paintings that will be displayed in each room is:
Question 16.
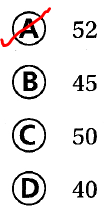
Factory workers pack 25 umbrellas in each box. If 1,300 umbrellas are shipped out, how many boxes were packed?
(A) 52
(B) 45
(C) 50
(D) 40
Answer:
It is given that
Factory workers pack 25 umbrellas in each box and 1,300 umbrellas are shipped out
Now,
According to the given information,
The number of boxes that were packed = 1,300 ÷ 25
Now,
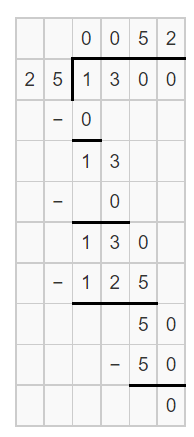
Hence, from the above,
We can conclude that
The number of boxes that were packed is:
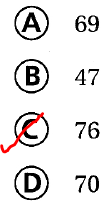
Question 17.
Multi-Step A store had 1,116 customers on Monday, 882 customers on Tuesday, and 1,194 customers on Wednesday. The store is open 14 hours each day. If the same number of customers arrived each hour during the three days, how many customers arrived each hour?
(A) 69
(B) 47
(C) 76
(D) 70
Answer:
It is given that
A store had 1,116 customers on Monday, 882 customers on Tuesday, and 1,194 customers on Wednesday. The store is open 14 hours each day and the same number of customers arrived each hour during the three days
So,
The total number of customers during the three days = 1,116 + 882 + 1,194
= 3,192 customers
So,
The number of customers arrived at each hour = 3,192 ÷ 42
Now,
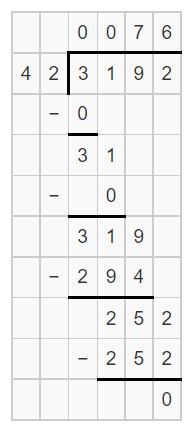
Hence, from the above,
We can conclude that
The number of customers who arrived at each hour is: