Refer to our Texas Go Math Grade 5 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 5 Lesson 12.5 Answer Key Compare Volumes.
Texas Go Math Grade 5 Lesson 12.5 Answer Key Compare Volumes
Essential Question
How can you use the strategy to make a table to compare different rectangular prisms with the same volume?
Answer:
When we have the volume of a rectangular prism the same but we want different dimensions,
Make the table of factors of the given volume and write the factors as different dimensions for the given rectangular prism that has the same volume
Unlock the Problem
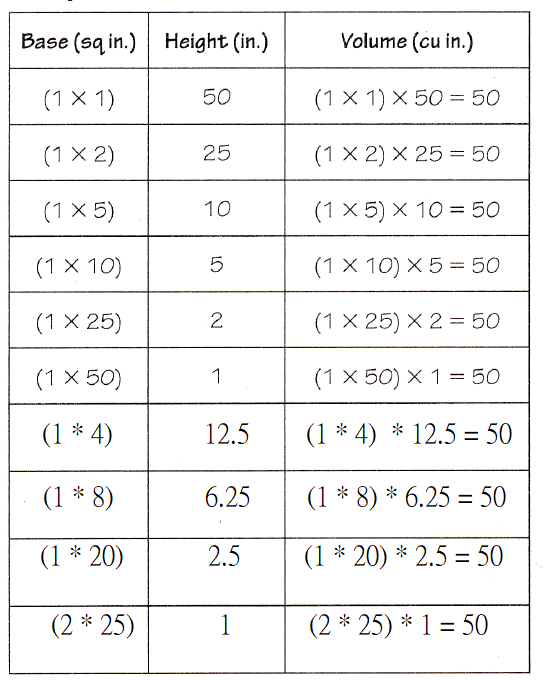
Adam has 50 one-inch cubes. The cubes measure 1 inch on each edge. Adam wonders how many rectangular prisms, each with a different-size base, that he could make with all of the one-inch cubes.
Read
What do I need to find?
I need to find the number of edges each with a different size, that has a volume of 50 one-inch cubes.
What information am I given?
I can use the formula of the volume of a rectangular prism and the factors of 50.
Plan
What is my plan or strategy?
I will use the formula and the factors of 50 in a table that shows all of the possible combinations of dimensions with a volume of 50 without repeating the dimensions of the bases.
Question 1.
What else do you need to do to solve the problem?
Answer:
We need the different factors of 50 to represent as dimensions of the rectangular prism to solve the problem
Question 2.
How many rectangular prisms with different bases can Adam make using fifty one-Inch cubes?
Answer:
We know that,
The factors of 50 are 1, 2, 5, 10, 25, and 50
Hence, from the above,
By using the factors,
We can conclude that
The number of rectangular prisms with different bases can Adam make using fifty one-Inch cubes is: 6 rectangular prisms
Solve.
Complete the table.
Try Another Problem
Mrs. Wilton is planning a rectangular flower box for her front window. She wants the flower box to hold exactly 16 cubic feet of soil. How many different flower boxes, all with whole-number dimensions and a different-size base, will hold exactly 16 cubic feet of soil?


Math Talk
Mathematical processes
Explain how a flower box with dimensions of (1 × 2) × 8 is different from a flower box with dimensions of (2 × 8) × 1.
Answer:
The given dimensions are: (1 × 2) × 8 and (2 × 8) × 1
Now,
From (1 × 2) × 8,
We can observe that
Length – 1 unit
Width – 2 units
Height – 8 units
Now,
From (2 × 8) × 1,
We can observe that
Length – 2 units
Width – 8 units
Height – 1 unit
Now,
When we observe the dimensions,
We can say that the heights are different
Hence, from the above,
We can conclude that
A flower box with dimensions of (1 × 2) × 8 is different in terms of height from a flower box with dimensions of (2 × 8) × 1
Question 3.
How many flower boxes with different-size bases will hold exactly 16 cubic feet of soil, using whole-number dimensions?
Answer:
The number of flower boxes with different-size bases that will hold exactly 16 cubic feet of soil is:
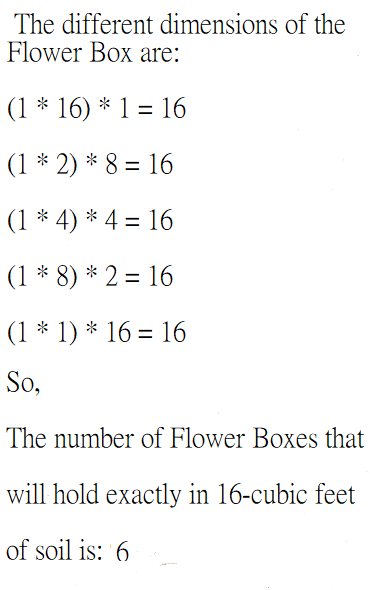
Hence, from the above,
We can conclude that
The number of flower boxes that will hold exactly 16-cubic feet of soil is: 6 flower boxes
Unlock the Problem
Share and Show
Question 1.
Mr. Price makes cakes that have a volume of 360 cubic inches. The cakes are 3 inches tall and have different whole number lengths and widths. No cakes have a length or width of 1 or 2 inches. How many different cakes, each with a different size base, have a volume of 360 cubic inches?
First, think about what you need to find and the information you have.
Next, make a table using the information from the problem.
Finally, use the table to solve the problem.
Answer:
It is given that
Mr. Price makes cakes that have a volume of 360 cubic inches. The cakes are 3 inches tall and have different whole number lengths and widths. No cakes have a length or width of 1 or 2 inches
Now,
We know that,
Volume = (Length × Width) × Height
Now,
The factors of 360 are:
1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 18, 20, 24, 30, 36, 40, 45, 60, 72, 90, 120, 180, and 360
Now,
It is also given that,
The width and length must not be 1 or 2 inches
The height of the cakes must be 3 inches
So,
The dimensions of the different cakes will be:
(3 × 40) × 3 = 360
(4 × 30) × 3 = 360
(5 × 24) × 3 = 360
(6 × 20) × 3 = 360
(8 × 15) × 3 = 360
(10 × 12) × 3 = 360
(15 × 8) × 3 = 360
(20 × 6) × 3 = 360
(24 × 5) × 3 = 360
(30 × 4) × 3 = 360
(40 × 3) × 3 = 360
Hence, from the above,
We can conclude that
The number of different cakes, each with a different size base, has a volume of 360 cubic inches is: 11
Question 2.
H.O.T. What if the 360 cubic-inch cakes are 4 inches thick and any whole number length and width are possible? How many different cakes could be made? Suppose that the cost of a cake that size is $25, plus $1.99 for every 4 cubic inches of cake. How much would the cake cost?

Answer:
We know that,
Volume = (Length × Width) × Height
Now,
The factors of 360 are:
1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 18, 20, 24, 30, 36, 40, 45, 60, 72, 90, 120, 180, and 360
Now,
It is given that
The height must be: 4 inches
The length and width must be any value from the given factors
So,
The different dimensions of the different cakes could be:
(1 × 90) × 4 = 360
(2 × 45) × 4 = 360
(3 × 30) × 4 = 360
(5 × 18) × 4 = 360
(6 × 15) × 4 = 360
(9 × 10) × 4 = 360
(10 × 9) × 4 = 360
(15 × 6) × 4 = 360
(18 × 5) × 4 = 360
(30 × 3) × 4 = 360
(45 × 2) × 4 = 360
(90 × 1) × 4 = 360
Now,
Let the cost of total cakes be: x
Now,
The total cost of cakes = $25 + $1.99x
= $25 + $1.99 (12)
= $25 + $13.88
= $38.88
Now,
The cost of each cake = \(\frac{$38.88}{4}\)
= $9.72
Hence, from the above,
We can conclude that
The number of different cakes that could be made is: 12 cakes
The cost of eaach cake is: $9.72
Question 3.
One company makes inflatable swimming pools that come in four sizes of rectangular prisms. The length of each pool is twice the width and twice the depth. The depth of the pools is each a whole number from 2 to 5 feet. If the pools are filled all the way to the top, what is the volume of each pool?
Answer:
It is given that
One company makes inflatable swimming pools that come in four sizes of rectangular prisms. The length of each pool is twice the width and twice the depth. The depth of the pools is each a whole number from 2 to 5 feet
Now,
Let the length of the pool be: lLet the width of the pool be: w
Let the depth of the pool be: h
Now,
Volume = Length × Width × Height
So,
The depth of the pools are: 2 feet, 3 feet, 4 feet, and 5 feet
Now,
For h = 2 feet,
l = 8 feet
w = 4 feet
h = 2 feet
So,
V = 8 × 4 × 2 = 64 ft³
For h = 3 feet,
l = 12 feet
w = 6 feet
h = 3 feet
So,
V = 12 × 6 × 3 = 216 ft³
For h = 4 feet,
l = 16 feet
w = 8 feet
h = 4 feet
So,
V = 8 × 4 × 16 = 512 ft³
For h = 5 feet,
l = 20 feet
w = 10 feet
h = 5 feet
So,
V = 20 × 10 × 5 = 1,000 ft³
Hence, from the above,
We can conclude that
For h = 2 feet, the volume of the pool is: 64 ft³
For h = 3 feet, the volume of the pool is: 216 ft³
For h = 4 feet, the volume of the pool is: 512 ft³
For h = 5 feet, the volume of the pool is: 1,000 ft³
Problem Solving
Question 4.
H.O.T. Multi-Step Kathy has ribbons that have lengths of 7 inches, 10 inches, and 12 inches. Explain how she can use these ribbons to measure a length of 15 inches.
Answer:
It is given that
Kathy has ribbons that have lengths of 7 inches, 10 inches, and 12 inches
Now,
Put the 10 inches and 12 inches end to end and then back off the 7 inches
So,
(10 + 12) – 7
= 22 – 7
= 15 inches
Hence, from the above,
We can conclude that
Put the 10 inches and 12 inches end to end and then back off the 7 inches
Daily Assessment Task
Fill in the bubble completely to show your answer.
Question 5.
Analyze Rhoda makes a platform using one-inch cubes. The platform is shaped like a rectangular prism and needs to be 4 inches tall. How many different platforms can Rhoda make using only 16 one-inch cubes?
(A) 2
(B) 3
(C) 4
(D) 5
Answer:
It is given that
Rhoda makes a platform using one-inch cubes. The platform is shaped like a rectangular prism and needs to be 4 inches tall
Now,
According to the given information,
The height of the platform must be: 4 inches
So,
The number of different platforms Rhoda can make using only 16-one inch cubes is:
(1 × 4) × 4 = 16
(2 × 2) × 4 = 16
(4 × 1) × 4 = 16
Hence, from the above,
We can conclude that
The number of different platforms Rhoda can make using only 16-one inch cubes is:

Question 6.
Selena is building a sculpture using 100 one-inch cubes. She wants the sculpture, which is shaped like a rectangular prism, to be 2 inches tall. Which of the following shows a dimension combination that Selena should NOT use?
(A) (25 × 2) × 2
(B) (50 × 1) × 2
(C) (10 × 5) × 2
(D) (10 × 10) × 2
Answer:
It is given that
Selena is building a sculpture using 100 one-inch cubes. She wants the sculpture, which is shaped like a rectangular prism, to be 2 inches tall
Now,
According to the given information,
The height of the rectangular peism must be: 2 inches
So,
The dimension combination that Selena should use is:
(1 × 50) × 2 = 100
(2 × 25) × 2 = 100
(5 × 10) × 2 = 100
(10 × 5) × 2 = 100
(25 × 2) × 2 = 100
(50 × 1) × 2 = 100
Hence, from the above,
We can conclude that
The dimension combination that Selena should not use is:

Question 7.
Multi-Step Jonah has 20 one-inch cubes and uses them all to create a rectangular prism. The height of the prism is 10 inches. Mila uses 20 one-inch cubes to make a rectangular prism that has a height of 2 inches. Which statement is true about the volumes of the two prisms?
(A) They do not have the same volume.
(B) The volumes are the same because both prisms are made using 20 one-inch cubes.
(C) The volumes are the same because Jonah and Mila used 20 cubes for an area of 20 square inches.
(D) The volume of the first prism is five times the volume of the second prism.
Answer:
It is given that
Jonah has 20 one-inch cubes and uses them all to create a rectangular prism. The height of the prism is 10 inches. Mila uses 20 one-inch cubes to make a rectangular prism that has a height of 2 inches.
Now,
According to the given information,
The volume of a rectangular prism created by Jonah = 20 × 10
= 40 × 5
= 200 inches³
The volume of a rectangular prism created by Mila = 20 × 2
= 40 inches³
Hence, from the above,
We can conclude that
The statements that are true about the volumes of the two prisms is:

Texas Test Prep
Question 8.
John is making a chest that will have a volume of 1,200 cubic inches. The length is 20 inches and the width is 12 inches. How many inches tall should his chest be?
(A) 6 in.
(B) 4 in.
(C) 5 in.
(D) 7 in.
Answer:
It is given that
John is making a chest that will have a volume of 1,200 cubic inches. The length is 20 inches and the width is 12 inches
Now,
Let the height of the chest be: x
Now,
According to the given information,
The volume of the chest = Length × Width × Height
So,
1,200 = 20 × 12 × x
x = \(\frac{1,200}{240}\)
x = 5
Hence, from the above,
We can conclude that
The height of the chest is:

Texas Go Math Grade 5 Lesson 12.5 Homework and Practice Answer Key
Question 1.
Cole has a rectangular prism that measures 4 inches by 5 inches by 6 inches. He says that by changing one dimension, he can make a prism with a volume of 240 cubic inches. What are the three ways Cole can do this?
Answer:
It is given that
Cole has a rectangular prism that measures 4 inches by 5 inches by 6 inches. He says that by changing one dimension, he can make a prism with a volume of 240 cubic inches
Now,
According to the given information,
The volume of the rectangular prism made by Cole = 4 × 5 × 6
= 120 inches³
Now,
To make a prism with a volume of 240 cubic inches,
We have to change only one dimension of the previous dimensions
So,
240 = (5 × 6) × 8
240 = (6 × 8) × 5
240 = (5 × 8) × 6
Hence, from the above,
We can conclude that
The three ways that Cole can make a prism with the volume of 240 cubic inches with the given dimensions and by changing only 1 dimension are:
(Length, Width, Height) —-> (5, 6, 8), (6, 8, 5), and (5, 8, 6)
Question 2.
Sydney wants to use centimeter cubes to build a rectangular prism with a length of 8 centimeters, a width of 10 centimeters, and a height of 6 centimeters. If the centimeter cubes come in packages of 100, how many packages does Sydney need to make the prism?
Answer:
It is given that
Sydney wants to use centimeter cubes to build a rectangular prism with a length of 8 centimeters, a width of 10 centimeters, and a height of 6 centimeters and the centimeter cubes come in packages of 100
Now,
According to the given information,
The volume of the rectangular prism = 8 × 10 × 6
= 480 cm³
Now,
The number of packages Sydney need to make the prism = \(\frac{480}{100}\)
≅ 5 packages
Hence, from the above,
We can conclude that
The number of packages Sydney need to make the prism is about 5 packages
Question 3.
Rhoda has 27 unit cubes. How many rectangular prisms with different-size bases can she make if she uses all the unit cubes in each prism?
Answer:
It is given that
Rhoda has 27 unit cubes
Now,
We know that,
The factors of 27 are 1, 3, 9, 27.
So,
According to the given information,
She can make 5 rectangular prisms of sizes 1 x 1 x 27 or 1 x 3 x 9 or 1 x 9 x 3 or 3 x 3 x 3 or 3 x 9 x 1
Hence, from the above,
We can conclude that
The number of rectangular prisms with different-size bases can she make if she uses all the unit cubes in each prism is: 5 rectangular prisms
Question 4.
Alejandro has 64 centimeter cubes. He uses them to build cubes with different side lengths. How many different cubes can he make? Explain.
Answer:
It is given that
Alejandro has 64 centimeter cubes. He uses them to build cubes with different side lengths. How many different cubes can he make
Now,
According to the given information,
The factors of 64 are: 1, 2, 4, 8, 16, 32, and 64
Now,
The number of different cubes Alejandro can amke with 64 cm cubes is:
(1 × 64) × 1 = 64
(2 × 32) × 1 = 64
(4 × 4) × 4 = 64
(8 × 1) × 8 = 64
(16 × 1) × 4 = 64
(32 × 1) × 2 = 64
(64 × 1) × 1 = 64
Hence, from the above,
We can conclude that
The number of different cubes Alejandro can amke with 64 cm cubes is: 7 cubes
Problem Solving
Question 5.
Aya builds a storage box that is 10 cm long, 12 cm wide, and 10 cm tall. She wants to build a second box that is 10 cm long and 20 cm tall. If the volume of both boxes is the same, how wide is the second box?
Answer:
It is given that
Aya builds a storage box that is 10 cm long, 12 cm wide, and 10 cm tall. She wants to build a second box that is 10 cm long and 20 cm tall and the volume of both boxes is the same
Now,
According to the given information,
The volume of the first box = 10 × 12 × 10 = 1,200 cm³
Now,
Let the unknown measurement be: x cm
So,
1,200 = 10 × 20 × x
x = \(\frac{1,200}{200}\)
x = 6 cm
Hence, from the above,
We can conclude that
The width of the second box is: 6 cm
Texas Test Prep
Lesson Check
Fill in the bubble completely to show your answer.
Question 6.
Dominic builds a rectangular prism using centimeter cubes. The volume of his prism is 60 cubic centimeters. Which of the following is NOT a possible combination of dimensions for the prism?
(A) (5 × 6) × 3
(B) (2 × 15) × 2
(C) (6 × 10) × 1
(D) (4 × 5) × 3
Answer:
It is given that
Dominic builds a rectangular prism using centimeter cubes. The volume of his prism is 60 cubic centimeters
Now,
According to the given information,
The product of the different dimensions must be equal to 60 cubic centimeters
Hence, from the above,
We can conclude that
The following that is not a possible combination of dimensions for the prism is:

Question 7.
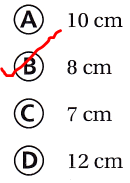
An architect makes a model of a building with a volume of 1,440 cubic centimeters. The length of the model is 15 centimeters and the width is 12 centimeters. How many centimeters tall is the model?
(A) 10 cm
(B) 8 cm
(C) 7 cm
(D) 12 cm
Answer:
It is given that
An architect makes a model of a building with a volume of 1,440 cubic centimeters. The length of the model is 15 centimeters and the width is 12 centimeters
Now,
Let the unknown measure ment be x
Now,
According to the given information,
Volume = Length × Width × Height
So,
1,440 = 15 × 12 × x
x = \(\frac{1,440}{15 × 12}\)
x = 8 cm
Hence, from the above,
We can conclude that
The height of the model is:
Question 8.
Erin designs a trophy stand using one-inch cubes. The stand is shaped like a rectangular prism. How many different stands can Erin design using exactly 12 one-inch cubes?
(A) 8
(B) 3
(C) 5
(D) 2
Answer:
It is given that
Erin designs a trophy stand using one-inch cubes. The stand is shaped like a rectangular prism
Now,
We know that,
The factors of 12 are: 1, 2, 3, 4, 6, and 12
Now,
The dimensions of different stands are:
(1 × 1) × 12 = 12
(2 × 3) × 2 = 12
(3 × 2) × 2 = 12
(2 × 2) × 3 = 12
(12 × 1) × 1 = 12
So,
According to the given information,
The number of different stands are: 6
Hence, from the above,
We can conclude that
The number of different stands Erin can design using exactly 12 one-inch cubes is:
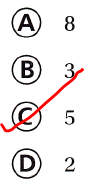
Question 9.
The volume of a rectangular prism is 140 cubic inches. How does that volume compare to the volume of a cube that measures 5 inches on each side?
(A) The rectangular prism’s volume is greater than the cube’s volume.
(B) The cube’s volume is greater than the rectangular prism’s volume.
(C) The volumes are equal.
(D) The rectangular prism’s volume is less than the cube’s volume.
Answer:
It is given that
The volume of a rectangular prism is 140 cubic inches
Now,
The Volume of the cube = Length × Width × Height
= 5 × 5 × 5
= 125 inches³
Hence, from the above,
We can conclude that
The statement that compares the volumes of the rectangular prism and the cube is:

Question 10.
Multi-Step Three rectangular prisms built using centimeter cubes have the following dimensions: Prism A: (6 × 7) × 5; Prism B: (7 × 4) × 6; Prism C: (6 × 8) × 4. Which lists the prisms in order from greatest to least volume?
(A) A; B; C
(B) B; C; A
(C) A; C; B
(D) C; A; B
Answer:
It is given that
Three rectangular prisms built using centimeter cubes have the following dimensions: Prism A: (6 × 7) × 5; Prism B: (7 × 4) × 6; Prism C: (6 × 8) × 4
Now,
According to the given information,
For Prism A:
Volume = (6 × 7) × 5 = 210 cubic units
For Prism B:
Volume = (7 × 4) × 6 = 168 cubic units
For Prism C:
Volume = (6 × 8) × 4 = 192 cubic unts
Hence, from the above,
We can conclude that
The list of the prisms from the greatest to the least volumes is:
Question 11.
Multi-Step Seth builds a rectangular prism with centimeter cubes with a length of 12 centimeters, a width of 6 centimeters, and a height of 4 centimeters. Seth adds more cubes to his prism, so the prism now has a height of 6 centimeters. If the base measurements stay the same, how many more cubes does Seth use?
(A) 72 cubes
(B) 288 cubes
(C) 144 cubes
(D) 78 cubes
Answer:
It is given that
Seth builds a rectangular prism with centimeter cubes with a length of 12 centimeters, a width of 6 centimeters, and a height of 4 centimeters. Seth adds more cubes to his prism, so the prism now has a height of 6 centimeters
Now,
Volume = 12 × 6 × 4
= 288 cm³
Now,
For a height pf 6 cm,
Volume = 12 × 6 × 6
= 432 cm³
Now,
The differenec beween the volumes with different heights = 432 – 288
= 144 cm³
Hence, from the above,
We can conclude that
The number of many more cubes does Seth use is:
