Refer to our Texas Go Math Grade 5 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 5 Lesson 12.2 Answer Key Understand Volume.
Texas Go Math Grade 5 Lesson 12.2 Answer Key Understand Volume
Essential Question
How can you use unit cubes to find the volume of a rectangular prism?
Answer:
To find the volume of a rectangular prism, multiply its 3 dimensions: length x width x height. The volume is expressed in cubic units
Investigate
Connect You can find the volume of a rectangular prism by counting unit cubes. Volume is the measure of the amount of space a solid figure occupies and is measured in cubic units. Each unit cube has a volume of 1 cubic unit.
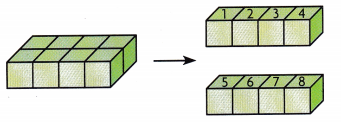
The rectangular prism above is made up of 8 unit cubes and has a volume of 8 cubic units.
Materials ![]() rectangular prism net A
rectangular prism net A ![]() centimeter cubes
centimeter cubes
A. Cut out, fold, and tape the net to form a rectangular prism.
B. Use centimeter cubes to fill the base of the rectangular prism without gaps or overlaps. Each centimeter cube has a length, width, and height of 1 centimeter and a volume of 1 cubic centimeter.
- How many centimeter cubes make up the length of the first layer? the width? the height?
length: 4 cm width: 5 cm height: 1 cm - How many centimeter cubes are used to fill the base?
Answer:
The number of centimeter cubes that are used to fill the base is: 20-centimeter cubes

C. Continue filling the rectangular prism, layer by layer. Count the number of centimeter cubes used for each layer.
- How many centimeter cubes are in each layer?
Answer:
The number of centimeter cubes present in each layer is: 5 cubes - How many layers of cubes fill the rectangular prism?
Answer:
The number of layers that filled the rectangular prism is: 4 layers - How many centimeter cubes fill the prism?
Answer:
The number of centimeter cubes that filled the prism is: 20- centimeter cubes
So,
The volume of the rectangular prism is 20 cubic centimeters.
Make Connections
To find the volume of three-dimensional figures, you measure in three directions. For a rectangular prism, you measure its length, width, and height. Volume is measured using cubic units, such as cubic centimeters or cubic inches. You can also write these as cu cm or cu in.
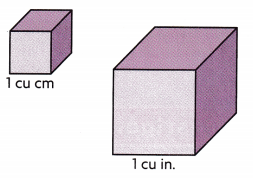
• Which has a greater volume, 1 cu cm or 1 cu in.? Explain.
Answer:
The given figures are:

Now,
From the given figures,
We can observe that
1 cu. inch cube is greater than 1 cu. cm
Hence, from the above,
We can conclude that
1 cu. inch has a greater volume than 1 cu. cm
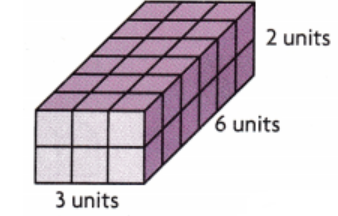
Find the volume of the prism if each cube represents 1 cu cm, 1 cu in, and 1 cu ft.
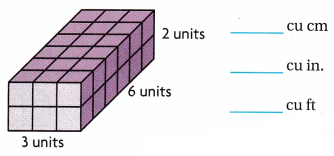
Answer:
The given figure is:
Now,
The volume of the given figure (V) = Length × Width × Height
= 3 × 6 × 2
= 36 cubic units
Hence, from the above,
We can conclude that
The volume of the given figure is: 36 cubic cm (or) 36 cubic inches (or) 36 cubic feet
Math Talk
Mathematical processes
Would the prism above be the same size if it were built with centimeter cubes, inch cubes, or foot cubes? Explain.
Answer:
We know that,
1 cm = 0.39 inches
1 cm = 0.032 feet
Hence,
The prisms will not be the same size if it were built with cubic cm, cubic in, or cubic foot
Share and Show
Question 1.
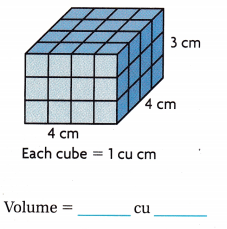
Answer:
The given figure is:
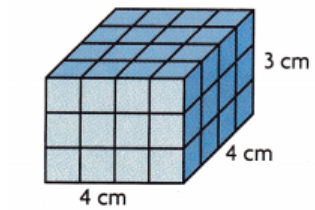
Now,
The volume of the given figure = Length × Width × height
= 4 × 4 × 3
= 48 cm³
Hence, from the above,
We can conclude that
The volume of the given figure is: 48 cm³
Question 2.
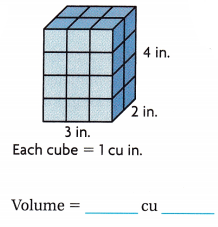
Answer:
The given figure is:
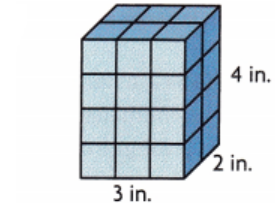
Now,
The volume of the given figure = Length × Width × height
= 2 × 4 × 3
= 24 in.³
Hence, from the above,
We can conclude that
The volume of the given figure is: 24 in.³
Compare the volumes. Write <, >, or =.
Question 3.
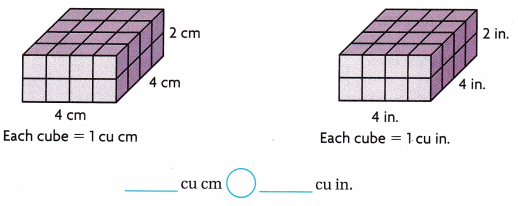
Answer:
The given figures are:

Now,
The volume of the first figure = 4 × 4 × 2
= 32 cm³
The volume of the second figure = 4 × 4 × 2
= 32 in.³
= 32 × 16.38 cm³
= 32 × 16 cm³
= 512 cm³
So,
32 cm³ < 512 cm³
Hence, from the above,
We can conclude that

Problem Solving
Question 4.
H.O.T. Connect What is the relationship between the number of centimeter cubes you used to fill each layer, the number of layers, and the volume of the prism on page 441?
Answer:
On page 441,
The volume of the prism is: 20 cubic units
The number of centimeter cubes in each layer is: 5
The number of layers is: 4
So,
The relationship between the number of centimeter cubes you used to fill each layer, the number of layers, and the volume of the prism on page 441 is:
The volume of the prism = (The number of layers) × (The number of centimeter cubes in each layer)
Hence, from the above,
We can conclude that
The relationship between the number of centimeter cubes you used to fill each layer, the number of layers, and the volume of the prism on page 441 is:
The volume of the prism = (The number of layers) × (The number of centimeter cubes in each layer)
Question 5.
H.O.T. If you had a rectangular prism that had a length of 3 units, a width of 4 units, and a height of 2 units, how many unit cubes would you need for each layer? How many unit cubes would you need to fill the rectangular prism?
Answer:
It is given that
You had a rectangular prism that had a length of 3 units, a width of 4 units, and a height of 2 units
So,
The number of cubes you would need for each layer = 3 × 4
= 12 cubes
So,
The number of cubes you need to fill the rectangular prism = 3 × 4 × 2
= 24 units³
Hence, from the above,
We can conclude that
The number of cubes you would need for each layer is: 12 cubes
The number of cubes you need to fill the rectangular prism is: 24 units³
Question 6.
H.O.T. What’s the Error? Al says that a cube with edges that measure 10 cm has a volume that is twice as much as a cube with sides that measure 5 cm. Explain and correct Al’s error.
Answer:
It is given that
Al says that a cube with edges that measure 10 cm has a volume that is twice as much as a cube with sides that measure 5 cm
Now,
The volume of the cube with side length 10 cm (x) = 10 × 10 × 10 = 1,000 cm³
The volume of the cube with side length 5 cm (y) = 5 × 5 × 5 = 125 cm³
Now,
\(\frac{x}{y}\) = \(\frac{1,000}{125}\)
= 8 times
Hence, from the above,
We can conclude that
Al’s error is:
A cube with edges that measure 10 cm has a volume that is twice as much as a cube with sides that measure 5 cm
The correct answer is:
A cube with edges that measure 10 cm has a volume that is eight times as much as a cube with sides that measure 5 cm
Question 7.
H.O.T. pia built a rectangular prism with cubes. The base of her prism has 12 cm cubes. If the prism was built with 108 cm cubes, what is the height of her prism?

Answer:
It is given that
Pia built a rectangular prism with cubes. The base of her prism has 12 cm cubes. The prism was built with 108 cm cubes
Now,
The volume of a rectangular prism = Length × Width × Height
108 = 12 × Height
Height = \(\frac{108}{12}\)
= 9 cm cubes
Hence, from the above,
We can conclude that
The height of Pia’s prism is: 9 cm cubes
Question 8.
Multi-Step A packing company makes boxes with edges each measuring 3 feet. What is the volume of a box? If 10 boxes are put in a shipping container and completely fill it with no gaps or overlaps, what is the volume of the shipping container?
Answer:
It is given that
A packing company makes boxes with edges each measuring 3 feet. and 10 boxes are put in a shipping container and completely fill it with no gaps or overlaps
Now,
The volume of a box = 3 × 3 × 3
= 27 feet³
So,
The volume of the shipping container = 27 × 10
= 270 feet³
Hence, from the above,
We can conclude that
The volume of a box is: 27 feet³
The volume of the shipping container is: 270 feet³
Daily Assessment Task
Fill in the bubble completely to show your answer.
Question 9.
Nabanita needs 140 cubes to make a model. The figure shows the number of cubes in a box. How many boxes of cubes does Nabanita need to buy so she has enough cubes for her model?
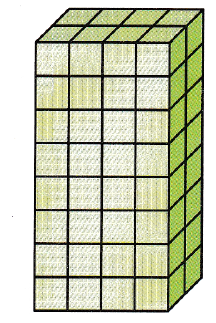
(A) 2 boxes
(B) 3 boxes
(C) 14 boxes
(D) 16 boxes
Answer:
It is given that
Nabanita needs 140 cubes to make a model. The figure shows the number of cubes in a box
Now,
The given figure is:

Now,
From the above figure,
We can observe that
The number of cubes in the given figure is: 32 cubes
Now,
We know that,
The number of boxes of cubes should be an integer
Now,
From the given options,
The number of boxes of cubes does Nabanita need to buy so she has enough cubes for her model = 32 + 3
= 35 boxes
Hence, from the above,
We can conclude that
The number of boxes of cubes does Nabanita need to buy so she has enough cubes for her model is:

Question 10.
A box is filled with speakers. Each speaker has a volume of 1 cubic foot. Ten speakers can fit in each layer and the height of the box is 4 feet. What is the volume of the box?
(A) 40 cubic feet
(B) 14 cubic feet
(C) 10 cubic feet
(D) 20 cubic feet
Answer:
It is given that
A box is filled with speakers. Each speaker has a volume of 1 cubic foot. Ten speakers can fit in each layer and the height of the box is 4 feet
So,
The volume of the box = 1 × 10 × 4
= 40 cubic feet
Hence, from the above,
We can conclude that
The volume of the box is:

Question 11.
Multi-Step A jewelry box has 3 drawers. Each drawer is 10 inches long, 5 inches wide, and 6 inches tall. Find the combined volume of the drawers.
(A) 11 cu.in
(B) 300 cu. in
(C) 33 cu. in
(D) 900 cu. in
Answer:
It is given that
A jewelry box has 3 drawers. Each drawer is 10 inches long, 5 inches wide, and 6 inches tall
Now,
The combined volume of the drawers = 3 × 10 × 5 × 6
= 900 cubic inches
Hence, from the above,
We can conclude that
The combined volume of the drawers is:

Texas Test Prep
Question 12.
Find the volume of the rectangular prism.
(A) 25 cubic feet
(B) 25 cubic meters
(C) 75 cubic meters
(D) 75 cubic centimeters
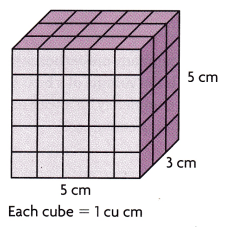
Answer:
The given figure is:
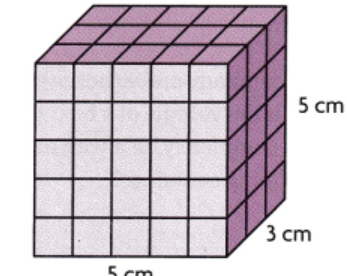
Now,
The volume of the given figure = 5 × 3 × 5
= 75 cm³
Hence, from the above,
We can conclude that
The volume of the given figure is:

Texas Go Math Grade 5 Lesson 12.2 Homework and Practice Answer Key
Question 1.
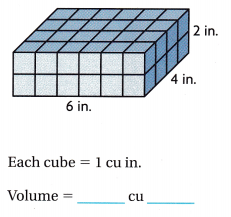
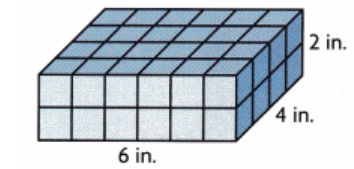
Answer:
The given figure is:
Now,
The volume of the given figure = Length × Width × Height
= 6 × 4 × 2
= 48 in.³
Hence, from the above,
We can conclude that
The volume of the given figure is: 48 in.³
Question 2.
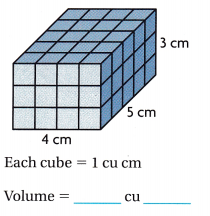
Answer:
The given figure is:
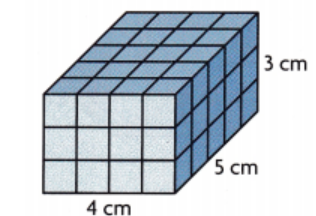
Now,
The volume of the given figure = Length × Width × Height
= 3 × 4 × 5
= 60 cm³
Hence, from the above,
We can conclude that
The volume of the given figure is: 60 cm³
Compare the volumes. Write <, >, or =
Question 3.
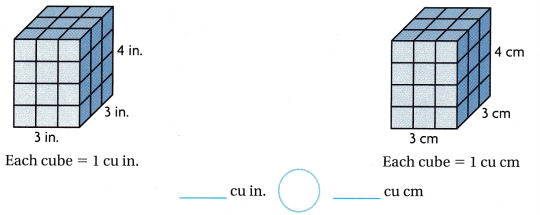
Answer:
The given figures are:

Now,
From the given figures,
We can observe that
The volume of the first figure = 3 × 3 × 4
= 36 in.³
The volume of the second figure = 3 × 3 × 4
= 36 cm³
= 36 × 0.06
= 2.16 in.³
Hence, from the above,
We can conclude that

Problem Solving
Question 4.
Salim built a rectangular prism with a length of 5 inches, a width of 4 inches, and a height of 3 inches. Would the prism Natalie built with a length of 3 inches, a width of 4 inches, and a height of 5 inches have the same volume or a different volume than Salim’s prism? Explain.
Answer:
It is given that
Salim built a rectangular prism with a length of 5 inches, a width of 4 inches, and a height of 3 inches. and the prism Natalie built with a length of 3 inches, a width of 4 inches, and a height of 5 inches
Now,
According to the given information,
The volume of a rectangular prism built by Salim = 5 × 4 × 3
= 60 in.³
The volume of a rectangular prism built by Natalie = 3 × 4 × 5
= 60 in.³
Hence, from the above,
We can conclude that
The volume of a rectangular prism built by Salim is the same as the volume of a rectangular prism built by Natalie
Question 5.
Oliver and Layla each built a rectangular prism with centimeter cubes. Both prisms have a volume of 24 cubic centimeters, but they do not look the same. Give possible dimensions for each prism.
Answer:
It is given that
Oliver and Layla each built a rectangular prism with centimeter cubes. Both prisms have a volume of 24 cubic centimeters, but they do not look the same
Now,
The dimensions of a rectangular prism built by Oliver with a volume of 24 cubic cm = 6 cm × 2 cm × 2 cm
The dimensions of a rectangular prism built by Layla with a volume of 24 cubic cm = 4cm × 2 cm × 3 cm
Hence, from the above,
We can conclude that
The dimensions of a rectangular prism built by Oliver with a volume of 24 cubic cm is: 6 cm × 2 cm × 2 cm
The dimensions of a rectangular prism built by Layla with a volume of 24 cubic cm is: 4cm × 2 cm × 3 cm
Lesson Check
Texas Test Prep
Fill in the bubble completely to show your answer.
Question 6.
Find the volume of the rectangular prism.
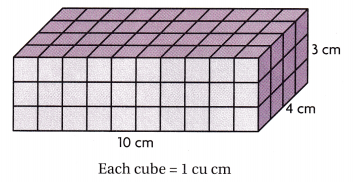
(A) 120 cubic inches
(B) 120 cubic centimeters
(C) 70 cubic inches
(D) 70 cubic centimeters
Answer:
The given figure is:

Now,
The volume of the given figure = Length × Width × Height
= 10 × 4 × 3
= 120 cm³
Hence, from the above,
We can conclude that
The volume of the given figure is:

Question 7.
Mason builds a tower with centimeter cubes for his design project. The figure below shows the part of the tower that he has completed so far.
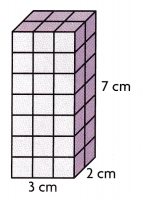
What does Mason need to do for the tower to have a volume of 54 cubic centimeters?
(A) Add one layer of cubes.
(B) Add 33 cubes.
(C) Add 2 cubes.
(D) Add two layers of cubes.
Answer:
It is given that
Mason builds a tower with centimeter cubes for his design project. The figure below shows the part of the tower that he has completed so far.
Now,
The given figure is:

Now,
From the given figure,
We can observe that
The number of cubes in each layer = 3 × 2 = 6 cubes
Now,
The volume of the tower = 3 × 2 × 7 = 42 cm³
Now,
The more cubes that ahve to be added by the mason = 54 – 42 = 12 cubes
Hence, from the above,
We can conclude that
The Mason needed to do for the tower to have a volume of 54 cubic centimeters is:

Question 8.
A chest is filled with toy blocks. Each block has a volume of 1 cubic foot. Twenty-five blocks fit in the bottom of the chest and the height of the chest is 3 feet. What is the volume of the chest?
(A) 75 cubic feet
(B) 60 cubic feet
(C) 28 cubic feet
(D) 25 cubic feet
Answer:
It is given that
A chest is filled with toy blocks. Each block has a volume of 1 cubic foot. Twenty-five blocks fit in the bottom of the chest and the height of the chest is 3 feet
Now,
Accordin to the given information,
The volume of the chest = 1 × 25 × 3
= 75 cubic feet
Hence, from the above,
We can conclude that
The volume of the chest is:

Question 10.
Multi-Step Lily serves 1-inch cheese cubes to her guests on a rectangular tray that is 6 inches long, 4 inches wide, and 2 inches tall. When the tray is only half full, what is the volume of the cheese cubes?
(A) 96 cu in.
(B) 12 cu in.
(C) 48 cu in.
(D) 24 cu in.
Answer:
It is given that
Lily serves 1-inch cheese cubes to her guests on a rectangular tray that is 6 inches long, 4 inches wide, and 2 inches tall
Now,
According to the given information,
The volume of the cheese cubes when the tray is full = 6 × 4 × 2
= 48 in³
Now,
The volume of the cheese cubes when the tray is only half-full = \(\frac{48}{2}\)
= 24 in³
Hence, from the above,
We can conclude that
The volume of the cheese cubes when the tray is only half-full is:

Question 11.
Multi-Step Fernando builds a rectangular prism with centimeter cubes. The length of the prism is 2 centimeters. The width is twice the length and the height is twice the width. What is the volume of Fernando’s prism?
(A) 48 cu cm
(B) 16 cu cm
(C) 8 cu cm
(D) 64 cu cm
Answer:
It is given that
Fernando builds a rectangular prism with centimeter cubes. The length of the prism is 2 centimeters. The width is twice the length and the height is twice the width
Now,
According to the given information,
The volume of Fernanado’s prism = Length × Width × Height
= 2 × 4 × 8
= 64 cm³
Hence, from the above,
We can conclude that
The volume of Fernando’s prism is:
