Refer to our Texas Go Math Grade 4 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 4 Lesson 5.1 Answer Key Add and subtract parts of a whole.
Texas Go Math Grade 4 Lesson 5.1 Answer Key Add and subtract parts of a whole
Essential Question
When con you odd or subtract ports of o whole?
Answer:
Explanation:
When the denominators are same
we can add or subtract
Materials
- fraction circles
- color pencils
Ms. Clark has the following pie pieces left over from a bake sale.

She will combine the pieces so they are on the same dish. How much pie will be on the dish?
Answer: \(\frac{2}{3}\)
Explanation:
\(\frac{4}{6}\) that is \(\frac{2}{3}\) pie will be on the dish
A. Model the problem using fraction circles. Draw a picture of your model. Then write the sum.
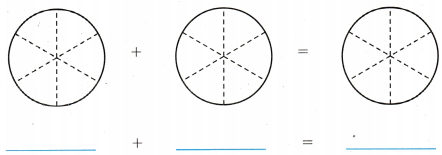
So, ___________ of a pie is on the dish.
Answer:
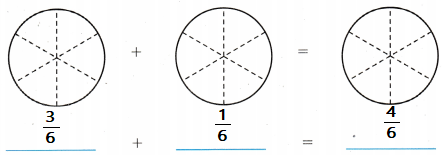
So, \(\frac{4}{6}\) of a pie is on the dish.
B. Suppose Ms. Clark eats 2 pieces of the pie. How much pie will be left on the dish? Model the problem using fraction circles. Draw a picture of your model. Then write the difference.
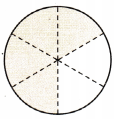
______________ – ____________ = ____________
So, _____________ of the pie is left on the dish.
Answer:
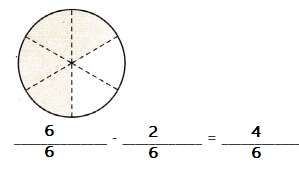
Explanation:
So, \(\frac{4}{6}\) of the pie is left on the dish.
Make connections
You can only join or separate parts that refer to the same whole.
Suppose Randy has \(\frac{1}{4}\) of a round cake and \(\frac{1}{4}\) of a square cake.
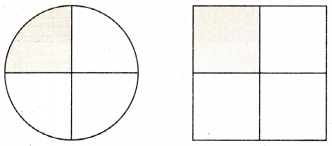
a. Are the wholes the same? Explain.
Answer: No,
Explanation:
Both the shapes are different.
The wholes are not same.
b. Does the sum \(\frac{1}{4}+\frac{1}{4}=\frac{2}{4}\) make sense in this situation? Explain.
Answer: No.
Explanation:
Both the shapes are different
The sum \(\frac{1}{4}+\frac{1}{4}=\frac{2}{4}\) make sense in this situation
Math Talk
Mathematical Processes
Give an example of a situation where the equation \(\frac{1}{4}+\frac{1}{4}=\frac{2}{4}\) makes sense. Explain your
Answer:
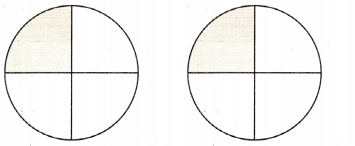
Explanation:
The equation \(\frac{1}{4}+\frac{1}{4}=\frac{2}{4}\) makes sense in this situation.
The whole is same when the shapes are same
Share and Grow
Use the model to write an equation.
Question 1.

Answer:
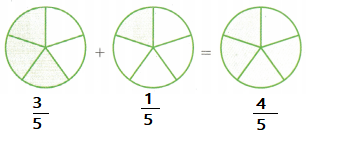
Explanation:
\(\frac{3}{5}\) + \(\frac{1}{5}\) = \(\frac{4}{5}\)
Question 2.
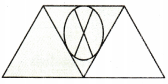
Answer:
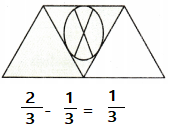
Explanation:
A trapezoid is divided into 3 triangles
In that 2 are shaded
1 part is not shaded
Question 3.
Multi-Step Sean has \(\frac{1}{5}\) of a cupcake and \(\frac{1}{5}\) of a large cake.
a. Are the wholes the same? Explain.
Answer: No,
Explanation:
The size cup cake and large cake are different.
b. Does the sum \(\frac{1}{5}+\frac{1}{5}\) = \(\frac{2}{5}\) make sense in this situation? Explain.
Answer: No,
Explanation:
Equation is correct but not in this situation.
Use the model to solve the equation.
Question 4.
\(\frac{3}{4}-\frac{1}{4}\) = _____________
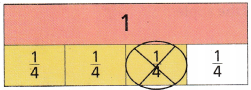
Answer: \(\frac{2}{4}\)
Explanation:
According to this equation \(\frac{3}{4}-\frac{1}{4}\) simplest form is \(\frac{2}{4}\)
Question 5.
\(\frac{5}{6}+\frac{1}{6}\) = _____________

Answer:
\(\frac{5}{6}+\frac{1}{6}\) = 1
Explanation:
When you divide a number with the same number the answer is 1.
Problem Solving
H.O.T. Sense or Nonsense?
Question 6.
Samantha and Kim used different models to help find \(\frac{1}{3}+\frac{1}{3}\) Whose model makes sense? Whose Model is nonsense? Explain your reasoning below each model.
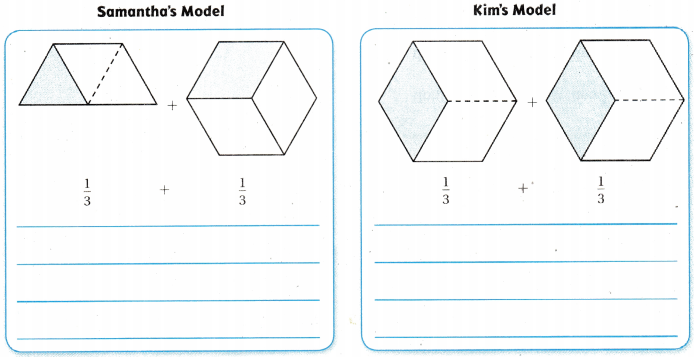
Answer:
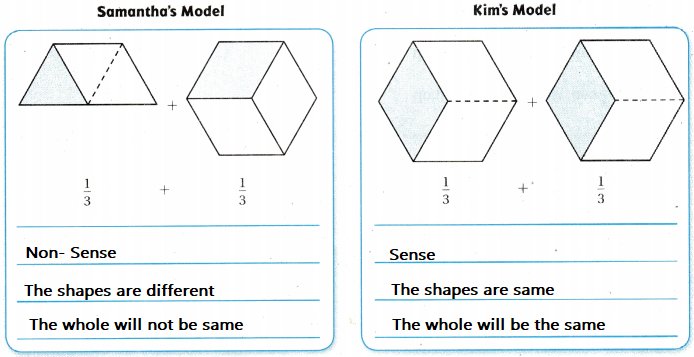
Explanation:
Kim’s model make sense.
Question 7.
H.O.T. Justify If there is \(\frac{4}{6}\) of a pie on a plate. what part of the pie is missing from the plate? Write an equation to justify your answer.
Answer:
\(\frac{4}{6}\) + \(\frac{2}{6}\) = 1
Explanation:
\(\frac{2}{6}\) of the pie is missing from the plate
Daily Assessment Task
Fill in the bubble completely to show your answer.
Use models to solve.
Question 8.
At lunch yesterday, Ryan ate \(\frac{2}{6}\) of an apple and I ate \(\frac{2}{6}\) of the apple. Together, how much of the apple did we eat?
(A) \(\frac{2}{6}\)
(B) \(\frac{4}{6}\)
(C) \(\frac{2}{12}\)
(D) \(\frac{4}{12}\)
Answer: B
Explanation:
\(\frac{2}{6}\) + \(\frac{2}{6}\) = \(\frac{4}{6}\)
\(\frac{4}{6}\) they ate the apple.
Question 9.
At the start of art class, Logan had \(\frac{7}{12}\) of a block of clay. After class, \(\frac{5}{12}\) of the block was left. What fraction of the block did Logan use during class?
(A) \(\frac{7}{12}\)
(B) \(\frac{12}{12}\)
(C) \(\frac{5}{12}\)
(D) \(\frac{2}{12}\)
Answer: D
Explanation:
\(\frac{7}{12}\) – \(\frac{5}{12}\) = \(\frac{2}{12}\)
Used the simplest form
Question 10.
Multi-Step Samantha is mixing batter for muffins. She mixes \(\frac{2}{4}\) cup of flour and \(\frac{1}{4}\) cup of sugar, Then she adds \(\frac{1}{4}\) cup of milk. How much muffin batter has she mixed so far?
(A) \(\frac{3}{8}\) cup
(B) \(\frac{2}{4}\) cup
(C) 1 cup
(D) \(\frac{3}{4}\) cup
Answer: C
Explanation:
\(\frac{2}{4}\) + \(\frac{1}{4}\) + \(\frac{1}{4}\) = 1
Used the simplest form
TEXAS Test Prep
Question 11.
Which equation matches the model?

(A) \(\frac{1}{4}+\frac{3}{4}=\frac{4}{4}\)
(B) \(\frac{1}{4}+\frac{2}{4}=\frac{3}{4}\)
(C) \(\frac{3}{4}+\frac{2}{4}=\frac{5}{4}\)
(D) \(\frac{1}{8}+\frac{2}{8}=\frac{3}{8}\)
Answer: B
Explanation:
\(\frac{1}{4}+\frac{2}{4}=\frac{3}{4}\) This equation matches the model
Texas Go Math Grade 4 Lesson 5.1 Homework and Practice Answer Key
Use the model to write an equation.
Question 1.

Answer:
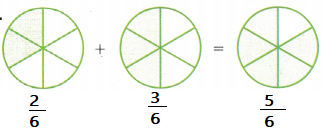
\(\frac{2}{6}\) + \(\frac{3}{6}\) = \(\frac{5}{6}\)
Explanation:
Written equation for above model.
Question 2.
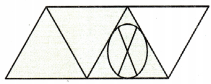
Answer:
\(\frac{3}{4}\) – \(\frac{1}{4}\) = \(\frac{2}{4}\)
Explanation:
The above parallelogram is divided into 4 equal parts in that 3 are shaded
in that 1 is filled with image
Use the model to solve an equation.
Question 3.
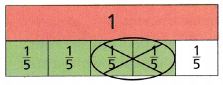
Answer: \(\frac{2}{5}\)
Explanation:
\(\frac{4}{5}\) – \(\frac{2}{5}\) = \(\frac{2}{5}\)
By using the model solved the equation.
Question 4.

Answer:
\(\frac{1}{4}\) + \(\frac{1}{4}\) = \(\frac{2}{4}\)
Explanation:
By using the model solved the equation.
Question 5.
If there is \(\frac{6}{8}\) of a pizza on a plate, what part of the pizza is missing from the plate? Write an equation to justify your answer.
Answer: \(\frac{2}{8}\)
Explanation:
1 – \(\frac{6}{8}\) = \(\frac{2}{8}\)
\(\frac{2}{8}\) part of the pizza is missing from the plate.
Problem Solving
Question 6.
If there is \(\frac{3}{8}\) of a pizza on a plate? what part of the pizza is missing from the plate? Write an equation to justify your answer.
Answer: \(\frac{5}{8}\)
Explanation:
1 – \(\frac{3}{8}\) = \(\frac{5}{8}\)
\(\frac{5}{8}\) part of the pizza is missing from the plate.
Question 7.
Maria is making cupcakes. She fills \(\frac{4}{12}\) of the cups with chocolate batter and \(\frac{7}{12}\) of the cups with vanilla batter. How many of the cups has Maria filled? Write an equation to justify your answer.
Answer: \(\frac{11}{12}\)
Explanation:
\(\frac{4}{12}\) + \(\frac{7}{12}\) = \(\frac{11}{12}\)
Maria filled \(\frac{11}{12}\) cups.
Lesson Check
Fill in the bubble completely to show your answer.
Question 8.
which equation matches the model?
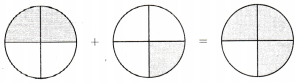
(A) \(\frac{2}{8}+\frac{1}{8}=\frac{3}{8}\)
(B) \(\frac{2}{4}+\frac{3}{4}=\frac{5}{4}\)
(C) \(\frac{2}{4}+\frac{1}{4}=\frac{3}{4}\)
(D) \(\frac{1}{4}+\frac{3}{4}=\frac{4}{4}\)
Answer: C
Explanation:
\(\frac{2}{4}+\frac{1}{4}=\frac{3}{4}\) equation matches the model
Question 9.
Which equation matches the model?
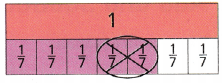
(A) \(\frac{5}{7}-\frac{2}{7}=\frac{3}{7}\)
(B) \(\frac{7}{7}-\frac{5}{7}=\frac{2}{7}\)
(C) \(\frac{7}{7}-\frac{2}{7}=\frac{5}{7}\)
(D) \(\frac{5}{7}-\frac{3}{7}=\frac{2}{7}\)
Answer: A
Explanation:
\(\frac{5}{7}-\frac{2}{7}=\frac{3}{7}\) equation matches the model
Question 10.
In Dylan’s family \(\frac{5}{6}\) of the children have brown hair. The rest of the children have blond hair.
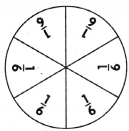
What fraction of the children has blond hair?
(A) \(\frac{4}{6}\)
(B) \(\frac{2}{6}\)
(C) \(\frac{3}{6}\)
(D) \(\frac{1}{6}\)
Answer: D
Explanation:
1 – \(\frac{5}{6}\) = \(\frac{1}{6}\)
\(\frac{1}{6}\) fraction of the children has blond hair
Question 11.
Miranda made a poster for her science project. She filled \(\frac{3}{8}\) of the poster with photos and \(\frac{4}{8}\) of the poster with written information. how much space has she filled on lier poster so far?
(A) \(\frac{7}{8}\)
(B) \(\frac{1}{8}\)
(C) \(\frac{6}{8}\)
(D) \(\frac{2}{8}\)
Answer: B
Explanation:
\(\frac{3}{8}\) + \(\frac{4}{8}\) = \(\frac{7}{8}\)
\(\frac{1}{8}\) space has she filled on lier poster so far
Question 12.
Multi-Step Carrie’s dance class learned \(\frac{1}{5}\) of a new dance on Monday, and \(\frac{2}{5}\) of the dance on Tuesday. What fraction of the dance is left for the class to learn on Wednesday?
(A) \(\frac{4}{5}\)
(B) \(\frac{3}{5}\)
(C) \(\frac{2}{5}\)
(D) \(\frac{1}{5}\)
Answer: D
Explanation:
\(\frac{1}{5}\) + \(\frac{2}{5}\) = \(\frac{3}{5}\)
1 – \(\frac{3}{5}\) = \(\frac{1}{5}\)
\(\frac{1}{5}\) fraction of the dance is left for the class to learn on Wednesday
Question 13.
Multi-Step Mrs. Simon planted \(\frac{4}{12}\) of her flowers in her front yard, \(\frac{3}{12}\) of her flowers in her back yard, and \(\frac{2}{12}\) of her flowers on the side of her house. What fraction of her flowers has she planted so far?
(A) \(\frac{2}{12}\)
(B) \(\frac{9}{12}\)
(C) \(\frac{3}{12}\)
(D) \(\frac{10}{12}\)
Answer: B
Explanation:
As the denominators are same
we can directly add the numerators
\(\frac{4}{12}\) + \(\frac{3}{12}\) + \(\frac{2}{12}\) = \(\frac{9}{12}\)