Refer to our Texas Go Math Grade 4 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 4 Lesson 4.1 Answer Key Compare Fractions Using Benchmarks.
Texas Go Math Grade 4 Lesson 4.1 Answer Key Compare Fractions Using Benchmarks
Essential Question
How can you use benchmarks to compare fractions?
Answer:
A benchmark is a reference number that can be used to compare two fractions. If one fraction is less than the benchmark and a second fraction is greater, the first fraction is less than the second.
Unlock the Problem
Zach made a popcorn snack. He mixed \(\frac{5}{8}\) gallon of popcorn with \(\frac{1}{2}\) gallon of dried apple rings. Did he use more dried apple rings or more popcorn?
Answer:
Zach used more dried apple rings.
Activity Compare \(\frac{5}{8}\) and \(\frac{1}{2}\).
Materials: fraction strips
Use traction strips to compare \(\frac{5}{8}\) and \(\frac{1}{2}\). Record on the model below.
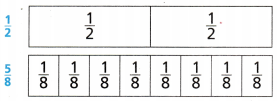
\(\frac{5}{8}\) ___________ \(\frac{1}{2}\)
So, Zach used more ______________ .
Answer:
\(\frac{5}{8}\) greater than \(\frac{1}{2}\)
So, Zach used more pop corn.
Explanation:
Math Talk
Mathematical Processes
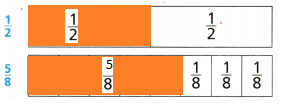
Explain how the number of eighth-size parts in \(\frac{5}{8}\) is related to the number of eighth-size parts you need to make \(\frac{1}{2}\).
Answer:
Explanation:
\(\frac{4}{8}\) = \(\frac{1}{2}\)
4 eighth size parts is equal to \(\frac{1}{2}\)
Benchmarks A benchmark is a known size or amount that helps you understand a different size or amount. You can use \(\frac{1}{2}\) as a benchmark to help you compare fractions.
Question 1.
How many eighths are equivalent to \(\frac{1}{2}\)?
Answer:
4 eighth size parts is equal to \(\frac{1}{2}\)

Question 2.
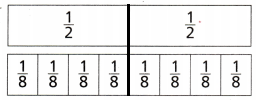
How can you compare \(\frac{5}{8}\) and \(\frac{1}{2}\) without using a model?
Answer:
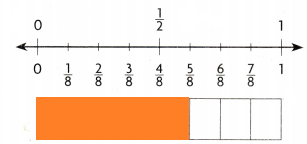
By using the bench mark.
Explanation:
By using the bench marks and compare the lengths with \(\frac{1}{2}\).
The shaded part is more than \(\frac{1}{2}\).
Example Use benchmarks to compare fractions.
A family hiked the same mountain trail. Evie and her father hiked \(\frac{5}{12}\) of the trail before they stopped for lunch. Jill and her mother hiked \(\frac{9}{10}\) of the trail before they stopped for lunch. Who hiked farther before lunch?
Answer:
Compare \(\frac{5}{12}\) and \(\frac{9}{10}\) to the benchmark \(\frac{1}{2}\).
Answer:
Step 1 Compare \(\frac{5}{12}\) to \(\frac{1}{2}\).
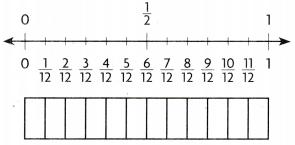
Think: Shade \(\frac{5}{12}\). \(\frac{5}{12}\) ___________ \(\frac{1}{2}\).
Answer:
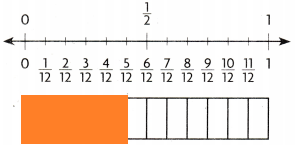
Explanation:
Shaded \(\frac{5}{12}\). \(\frac{5}{12}\) lesser than \(\frac{1}{2}\).
Step 2 Compare \(\frac{9}{10}\) to \(\frac{1}{2}\).
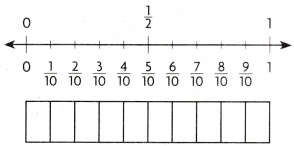
Think: Shade \(\frac{9}{10}\). \(\frac{9}{10}\) ___________ \(\frac{1}{2}\).
Answer:
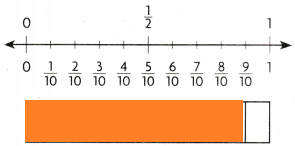
Explanation:
Shaded \(\frac{9}{10}\). \(\frac{9}{10}\) is greater than \(\frac{1}{2}\).
Since \(\frac{5}{12}\) is _____________ than \(\frac{1}{2}\) and is \(\frac{9}{10}\) than \(\frac{1}{2}\), you know that \(\frac{5}{12}\) ___________ \(\frac{9}{10}\).
So, _____________ hiked farther before lunch.
Answer:
Since \(\frac{5}{12}\) is lesser than \(\frac{1}{2}\) and \(\frac{9}{10}\) is greater than \(\frac{1}{2}\), you know that \(\frac{5}{12}\) lesser than \(\frac{9}{10}\).
So, Jill and her mother hiked farther before lunch.
Share and show
Question 1.
Compare \(\frac{2}{5}\) and \(\frac{1}{8}\). Write < or >.
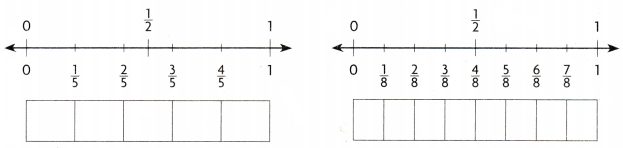
\(\frac{2}{5}\) ______________ \(\frac{1}{8}\)
Answer:
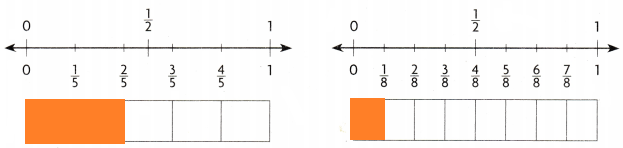
Explanation:
\(\frac{2}{5}\) greater than \(\frac{1}{8}\)
Shaded part represent the area covered
Compare. Write < or >.
Question 2.
\(\frac{1}{2}\) ______________ \(\frac{4}{6}\)
Answer:
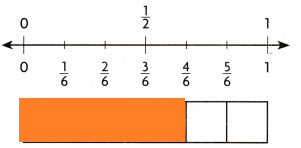
Explanation:
\(\frac{1}{2}\) is greater than \(\frac{4}{6}\)
The shaded part is more than \(\frac{1}{2}\)
Question 3.
\(\frac{3}{10}\) ______________ \(\frac{1}{2}\)
Answer:
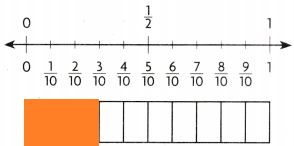
Explanation:
\(\frac{3}{10}\) is lesser than \(\frac{1}{2}\)
The shaded part is less than \(\frac{1}{2}\)
Question 4.
\(\frac{1}{2}\) ______________ \(\frac{4}{8}\)
Answer:
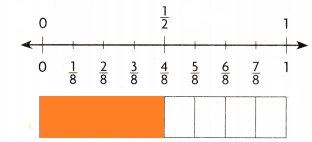
Explanation:
\(\frac{1}{2}\) is equal to \(\frac{4}{8}\)
Question 5.
\(\frac{5}{8}\) ______________ \(\frac{2}{5}\)
Answer:
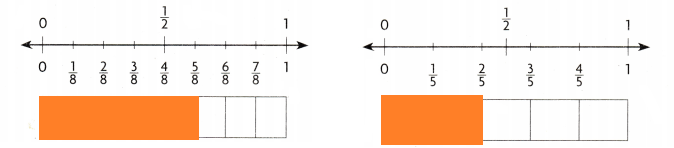
Explanation:
\(\frac{5}{8}\) is greater than \(\frac{2}{5}\)
H.O.T. Algebra Find a numerator that makes the statement true.
Question 6.
\(\frac{2}{4}\) < \(\frac{}{6}\)
Answer:
\(\frac{2}{4}\) < \(\frac{5}{6}\)
Explanation:
\(\frac{2}{4}\) is equal to \(\frac{1}{2}\) and \(\frac{5}{6}\) is greater than \(\frac{1}{2}\)
Question 7.
\(\frac{8}{10}\) < \(\frac{}{8}\)
Answer:
\(\frac{8}{10}\) < \(\frac{8}{8}\)
Explanation:
\(\frac{8}{10}\) is greater than \(\frac{1}{2}\) and \(\frac{8}{8}\) is equal to 1 so greater than \(\frac{8}{10}\)
Question 8.
\(\frac{10}{12}\) < \(\frac{}{4}\)
Answer:
\(\frac{10}{12}\) < \(\frac{4}{4}\)
Explanation:
\(\frac{10}{12}\) is greater than \(\frac{1}{2}\) and \(\frac{4}{4}\) is equal to 1 so greater than \(\frac{10}{12}\)
Question 9.
\(\frac{2}{5}\) < \(\frac{}{10}\)
Answer:
\(\frac{2}{5}\) < \(\frac{6}{10}\)
Explanation:
\(\frac{8}{10}\) is greater than \(\frac{1}{2}\) and \(\frac{8}{8}\) is equal to so greater than \(\frac{8}{10}\)
Question 10.
When two fractions are between 0 and \(\frac{1}{2}\) how do you know which fraction is greater? Explain.
Answer:
The lesser fraction is less than \(\frac{1}{2}\)
Explanation:
The greater fraction is more than \(\frac{1}{2}\) or equal to 1
Problem Solving
Question 11.
A group of students ate \(\frac{5}{12}\) of a large pepperoni pizza and \(\frac{8}{10}\) of a large cheese pizza. Did they eat more pepperoni pizza or cheese pizza?
Answer:
They eat more cheese pizza
Explanation:
\(\frac{8}{10}\) is greater than \(\frac{5}{12}\) compared with \(\frac{1}{2}\)
Question 12.
H.O.T. Saundra ran \(\frac{7}{12}\) of a mile. Lamar ran \(\frac{3}{4}\) of a mile. Who ran farther? Explain.
Answer:
Lamar ran farther than Saundra
Explanation:
\(\frac{3}{4}\) is greater than \(\frac{7}{12}\)
Question 13.
H.O.T. What’s the Question? Selena ran farther than Manny.
Answer:
Salena ran \(\frac{8}{10}\) and Manny ran \(\frac{4}{10}\)
Explanation:
The statement says that Selena ran more than Manny
\(\frac{8}{10}\) and \(\frac{4}{10}\) both the equations are compared with \(\frac{1}{2}\)
Question 14.
Mary made a small pan of ziti and a small pan of lasagna. She cut the ziti into 8 equal parts and the lasagna into 9 equal parts. Her family ate \(\frac{2}{3}\) of the lasagna. If her family ate more lasagna than ziti, what fraction of the ziti could have been eaten?
Answer:
\(\frac{2}{3}\) is the simplest form for \(\frac{6}{9}\)
so, they eat \(\frac{6}{9}\) of lasagna
Explanation:
They could have eaten \(\frac{3}{8}\)
\(\frac{6}{9}\) is greater than \(\frac{1}{2}\) and \(\frac{3}{8}\) is lesser than \(\frac{1}{2}\)
Daily Assessment Task
Fill in the bubble completely to show your answer.
Question 15.
Use Diagrams Some monkeys live high up in trees. Two monkeys are climbing a tree. One monkey climbed up \(\frac{5}{6}\) of the tree. The other monkey climbed up \(\frac{7}{8}\) of the tree. Which statement about \(\frac{5}{6}\) and \(\frac{7}{8}\) is true?
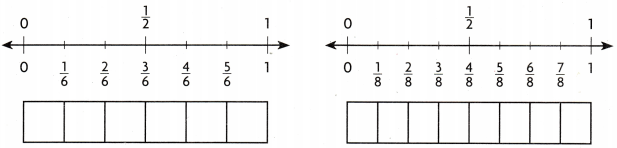
(A) \(\frac{5}{6}\) > \(\frac{7}{8}\)
(B) \(\frac{7}{8}\) < \(\frac{5}{6}\)
(C) \(\frac{5}{6}\) < \(\frac{7}{8}\)
(D) \(\frac{5}{6}\) = \(\frac{7}{8}\)
Answer: D
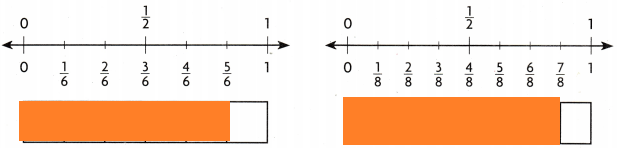
Explanation:
\(\frac{5}{6}\) = \(\frac{7}{8}\) is the statement true
because their shaded parts are equal
Question 16.
Maggie did \(\frac{5}{12}\) of her homework before dinner. Her brother did \(\frac{4}{10}\) of his homework. Which statement is true about the fractions \(\frac{5}{12}\) and \(\frac{4}{10}\)?

(A) \(\frac{5}{12}\) < \(\frac{4}{10}\)
(B) \(\frac{4}{10}\) = \(\frac{1}{2}\)
(C) \(\frac{5}{12}\) > \(\frac{4}{10}\)
(D) \(\frac{5}{12}\) > \(\frac{1}{2}\)
Answer: C
Explanation:
\(\frac{5}{12}\) > \(\frac{4}{10}\) is the statement true
Question 17.
Multi-Step If you know that \(\frac{2}{6}\) < \(\frac{1}{2}\) and \(\frac{3}{4}\) > \(\frac{1}{2}\), what do you know
(A) \(\frac{3}{4}\) = \(\frac{1}{2}\)
(B) \(\frac{2}{6}\) > \(\frac{3}{4}\)
(C) \(\frac{2}{6}\) > \(\frac{1}{2}\)
(D) \(\frac{2}{6}\) < \(\frac{3}{4}\)
Answer: D
Explanation:
\(\frac{2}{6}\) < \(\frac{3}{4}\) is the statement
Both the fractions are compared with \(\frac{1}{2}\)
TEXAS Test Prep
Question 18.
Todd is using the benchmark \(\frac{1}{2}\) to compare fractions. Which statement is NOT correct?
(A) \(\frac{5}{6}\) < \(\frac{1}{2}\)
(B) \(\frac{3}{6}\) = \(\frac{1}{2}\)
(C) \(\frac{5}{6}\) > \(\frac{1}{2}\)
(D) \(\frac{5}{6}\) ≠ \(\frac{1}{2}\)
Answer: A
Explanation:
\(\frac{5}{6}\) < \(\frac{1}{2}\) is the statement which is not true
Texas Go Math Grade 4 Lesson 4.1 Homework and Practice Answer Key
Compare Fractions Using Benchmarks
Question 1.
How many sixths are equivalent to \(\frac{1}{2}\)?
Answer:
Three sixths are equal to \(\frac{1}{2}\)
Explanation:
\(\frac{3}{6}\) = \(\frac{1}{2}\) we have to do the simplest form.
Question 2.
How can you compare \(\frac{7}{10}\) and \(\frac{1}{2}\) without using a model?
Answer:
By doing the simplest form
five tenths are to \(\frac{1}{2}\)
Explanation:
so we can easily compare by simplest form.
Compare. Write < or >.
Question 3.
\(\frac{8}{10}\) ___________ \(\frac{3}{8}\)
Answer:
\(\frac{8}{10}\) > \(\frac{3}{8}\)
Explanation:
Both the fractions are compared with \(\frac{1}{2}\)
Question 4.
latex]\frac{1}{3}[/latex] _____________ \(\frac{7}{12}\)
[Answer:
latex]\frac{1}{3}[/latex] < \(\frac{7}{12}\)
Explanation:
Both the fractions are compared with \(\frac{1}{2}\)
Question 5.
\(\frac{2}{6}\) _____________ \(\frac{7}{8}\)
Answer:
\(\frac{2}{6}\) < \(\frac{7}{8}\)
Explanation:
Both the fractions are compared with \(\frac{1}{2}\)
Question 6.
\(\frac{3}{4}\) _____________ \(\frac{1}{2}\)
Answer:
\(\frac{3}{4}\) > \(\frac{1}{2}\)
Explanation:
Both the fractions are compared with \(\frac{1}{2}\)
Question 7.
\(\frac{6}{6}\) _____________ \(\frac{1}{3}\)
Answer:
\(\frac{6}{6}\) > \(\frac{1}{3}\)
Explanation:
Both the fractions are compared with \(\frac{1}{2}\)
Question 8.
\(}[/\frac{4}{5latex] _____________ [latex]\frac{1}{6}\)
Answer:
\(}[/\frac{4}{5latex] > [latex]\frac{1}{6}[/latexExplanation:
Both the fractions are compared with [latex]\frac{1}{2}\)
Find a numerator that makes the statement true.
Question 9.
\(\frac{2}{4}\) > \(\frac{}{8}\)
Answer:
\(\frac{2}{4}\) > \(\frac{3}{8}\)
Explanation:
Both the fractions are compared with \(\frac{1}{2}\)
Question 10.
\(\frac{5}{10}\) > \(\frac{}{8}\)
Answer:
\(\frac{5}{10}\) > \(\frac{3}{8}\)
Explanation:
Both the fractions are compared with \(\frac{1}{2}\)
Question 11.
\(\frac{3}{6}\) > \(\frac{}{12}\)
Answer:
\(\frac{3}{6}\) > \(\frac{1}{12}\)
Explanation:
Both the fractions are compared with \(\frac{1}{2}\)
Question 12
\(\frac{2}{8}\) > \(\frac{}{10}\)
Answer:
\(\frac{2}{8}\) > \(\frac{1}{10}\)
Explanation:
Both the fractions are compared with \(\frac{1}{2}\)
Problem Solving
Question 13.
Leticia read \(\frac{4}{5}\) other book and Grace read \(\frac{6}{10}\) of her book. Who read more of her book, Leticia or Grace? Explain.
Answer:
Leticia read more
Explanation:
Both the fractions are compared with \(\frac{1}{2}\)
\(\frac{6}{10}\) is made as simplest form of \(\frac{3}{5}\)
\(\frac{3}{5}\) and \(\frac{4}{5}\) are compared so \(\frac{6}{10}\) is lesser and \(\frac{4}{5}\) is greater
Question 14.
Kyle made brownies and a cake. He cut the brownies into 6 equal parts and the cake into 8 equal parts. His family ate \(\frac{3}{4}\) of the cake. If his family ate more cake than brownies, what fraction of the brownies could have been eaten?
Answer:
\(\frac{3}{6}\)
Explanation:
\(\frac{3}{6}\) is equal to \(\frac{1}{2}\)
and \(\frac{3}{4}\) is greater than \(\frac{1}{2}\)
Lesson Check
Fill in the bubble completely to show your answer.
Question 15.
Which symbol completes the following statement?
\(\frac{5}{8}\) __________ \(\frac{9}{10}\)
(A) =
(B) ≠
(C) <
(D) >
Answer: C
Explanation:
\(\frac{5}{8}\) < \(\frac{9}{10}\)
lesser than symbol is used
Question 16.
Garrett is using the benchmark \(\frac{1}{2}\) to compare fractions. Which statement is NOT true?
(A) \(\frac{4}{8}\) = \(\frac{1}{2}\)
(B) \(\frac{3}{8}\) ≠ \(\frac{1}{2}\)
(C) \(\frac{3}{8}\) < \(\frac{1}{2}\)
(D) \(\frac{3}{8}\) > \(\frac{1}{2}\)
Answer: D
Explanation:
\(\frac{3}{8}\) > \(\frac{1}{2}\) is not correct statement.
Question 17.
Rob’s paper route is \(\frac{8}{10}\) mile long. Lin’s route is \(\frac{3}{4}\) mile long. What is true about \(\frac{8}{10}\) and \(\frac{3}{4}\)?
(A) \(\frac{3}{4}\) > \(\frac{8}{10}\)
(B) \(\frac{8}{10}\) < \(\frac{3}{4}\)
(C) \(\frac{8}{10}\) > \(\frac{3}{4}\)
(D) \(\frac{8}{10}\) = \(\frac{3}{4}\)
Answer: C
Explanation:
\(\frac{8}{10}\) > \(\frac{3}{4}\) is the statement true about \(\frac{8}{10}\) and \(\frac{3}{4}\)
Question 18.
Tia compares \(\frac{11}{12}\) and \(\frac{2}{3}\). Which statement
is true?
(A) \(\frac{2}{3}\) = \(\frac{11}{12}\)
(B) \(\frac{2}{3}\) > \(\frac{11}{12}\)
(C) \(\frac{11}{12}\) = \(\frac{2}{3}\)
(D) \(\frac{2}{3}\) < \(\frac{11}{12}\)
Answer: D
Explanation:
\(\frac{2}{3}\) < \(\frac{11}{12}\) is true about the statement of \(\frac{11}{12}\) and \(\frac{2}{3}\)
Question 19.
Multi-Step Sandra is making crafts from leftover ribbons. She needs a ribbon longer than \(\frac{2}{3}\) yard to make a bow. Which length of ribbon could she use for the bow?
(A) \(\frac{3}{4}\) yard
(B) \(\frac{2}{6}\) yard
(C) \(\frac{1}{5}\) yard
(D) \(\frac{4}{7}\) yard
Answer: A
Explanation:
\(\frac{3}{4}\) yard of ribbon she use for the bow
Question 20.
Multi-Step Jessie has several bottles of used paint. He has three bottles of blue paint. The first bottle is \(\frac{1}{8}\) full, the second bottle is \(\frac{1}{4}\) full, and the third bottle \(\frac{1}{4}\) is full He has one bottle of yellow paint that is \(\frac{1}{2}\) full. Which of the following correctly compares the blue paint to the yellow paint?
(A) \(\frac{3}{8}\) = \(\frac{1}{2}\)
(B) \(\frac{5}{8}\) > \(\frac{1}{2}\)
(C) \(\frac{3}{8}\) > \(\frac{1}{2}\)
(D) \(\frac{3}{8}\) < \(\frac{1}{2}\)
Answer: B
Explanation:
\(\frac{5}{8}\) > \(\frac{1}{2}\)
we make the unlike denominator to like denominators
and the added the numerators
and compared with \(\frac{1}{2}\)