Refer to our Texas Go Math Grade 4 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 4 Lesson 3.2 Answer Key Generate Equivalent Fractions.
Texas Go Math Grade 4 Lesson 3.2 Answer Key Generate Equivalent Fractions
Essential Question
How con you use multiplication to find equivalent fractions?
Answer:
Unlock the Problem
Patty needs \(\frac{3}{4}\) cup of dish soap to make homemade bubble solution. Her measuring cup is divided into eighths. What fraction of the measuring cup should Patty fill with dish soap?
Answer:
• Is an eighth-size part of a measuring cup bigger or smaller than a fourth-size part?
Answer:
Find how many eighths are in \(\frac{3}{4}\)
STEP 1 Compare fourths and eighths.

You need _________ eighth-size parts to make 1 fourth-size part.
Answer:
STEP 2. Find how many eighths you need to make 3 fourths.

You needed 2 eighth-size parts to make 1 fourth-size part.
So, you need __________ eighth-size parts to make 3 fourth-size parts.
So, Patty should fill \(\frac{}{8}\) of the measuring cup with dish soap.
Answer:
Math Talk
Mathematical Processes
How did you know how many eighth-size parts you needed to make 1 fourth-size part? Explain.
Answer:
Question 1.
Explain why 6 eighth-size parts is the same amount as 3 fourth-size parts.
Answer:
Example Write two fractions that are equivalent to \(\frac{1}{2}\)

So, \(\frac{1}{2}\) = ________ = ________
Answer:
Question 2.
Look at the model that shows \(\frac{1}{2}\) = \(\frac{3}{6}\) How does the number of parts in the whole affect the number of parts that are shaded? Explain.
Answer:
Math Talk
Mathematical Processes
Explain how you can use multiplication to write a fraction that is equivalent to \(\frac{3}{5}\)
Answer:
Share and Show
Question 1.
write a fraction that is equivalent to \(\frac{1}{3}\).

Answer:
Write two equivalent fractions.
Question 2.
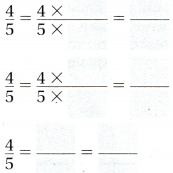
Answer:
Question 3.
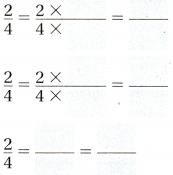
Answer:
Problem Solving
Use the recipe for 4-6.

Question 4.
Apply How could you use a \(\frac{1}{8}\)-cup measuring cup to measure the cornstarch?
Answer:
Question 5.
How could you use a \(\frac{1}{8}\)-cup measuring cup to measure the water?
Answer:
Question 6.
H.O.T. Kim says the amount of flour in the recipe can be expressed as a fraction. Is she correct? Explain.
Answer:
Question 7.
Write Math Explain using words how you know a fraction is equivalent to another fraction.
Answer:
Question 8.
Multi-Step Marcus needs \(\frac{3}{4}\) cup of sugar. Marcus said he could not measure out the sugar using a \(\frac{1}{6}\)-cup measuring cup. Explain why not and suggest what size measuring cup will work.
Answer:
Daily Assessment Task
Pill In the bubble completely to show your answer.
Question 9.
Ten trees are growing in Cindy’s yard. Of those, \(\frac{3}{5}\) are pine trees. Which fraction is equivalent to \(\frac{3}{5}\)?
(A) \(\frac{10}{10}\)
(B) \(\frac{5}{10}\)
(C) \(\frac{6}{10}\)
(D) \(\frac{1}{10}\)
Answer:
Question 10.
Clara read \(\frac{2}{3}\) of a book. Which fraction is equivalent to what Clara read?
(A) \(\frac{5}{6}\)
(B) \(\frac{4}{9}\)
(C) \(\frac{6}{9}\)
(D) \(\frac{2}{6}\)
Answer:
Question 11.
Multi-Step Ana uses equivalent amounts of seeds and corn to fill her bird feeder. Which could be the amount of seeds and corn that Ana uses?
(A) \(\frac{1}{4}\) cup seeds, \(\frac{1}{8}\) cup corn
(B) \(\frac{1}{4}\) cup seeds, \(\frac{2}{8}\) cup corn
(C) \(\frac{3}{4}\) cup seeds, \(\frac{3}{8}\) cup corn
(D) \(\frac{3}{4}\) cup seeds, \(\frac{7}{8}\) cup corn
Answer:
TEXAS Test Prep
Question 12.
Raul needs a piece of rope \(\frac{2}{3}\)yard long. Which fraction is equivalent to \(\frac{2}{3}\)?
(A) \(\frac{8}{15}\)
(B) \(\frac{6}{12}\)
(C) \(\frac{8}{12}\)
(D) \(\frac{4}{5}\)
Answer:
Texas Go Math Grade 4 Lesson 3.2 Homework and Practice Answer Key
Write two equivalent fractions.
Question 1.
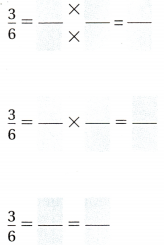
Answer:
Question 2.
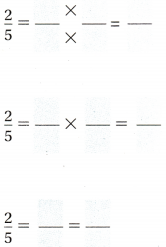
Answer:
Problem Solving
Use the recipe for 3-4.
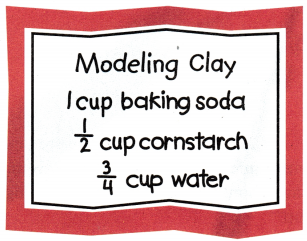
Question 3.
How could you use a \(\frac{1}{4}\)-cup measuring cup to measure the water?
Answer:
Question 4.
How could you use a \(\frac{1}{4}\)-cup measuring cup to measure the cornstarch?
Answer:
Lesson Check
Fill in the bubble completely to show your answer.
Question 5.
Which two fractions are equivalent to \(\frac{3}{10}\)?
(A) \(\frac{6}{30}, \frac{9}{10}\)
(B) \(\frac{1}{5}, \frac{3}{15}\)
(C) \(\frac{6}{20}, \frac{9}{30}\)
(D) \(\frac{12}{14}, \frac{6}{7}\)
Answer:
Question 6.
Sophie needs a piece of rope that is \(\frac{3}{4}\) yard long. Which fraction is equivalent to \(\frac{3}{4}\)?
(A) \(\frac{9}{10}\)
(B) \(\frac{4}{3}\)
(C) \(\frac{4}{5}\)
(D) \(\frac{6}{12}\)
Answer:
Question 7.
Theo needs to measure \(\frac{3}{4}\) cup of water He has a \(\frac{1}{8}\)-cup measuring cup. How many \(\frac{1}{8}\) cups are in \(\frac{3}{4}\) cup?
(A) 4
(B) 8
(C) 6
(D) 3
Answer:
Question 8.
Sandra finished \(\frac{1}{3}\) of her homework problems. Which fraction is equivalent to what Sandra finished?
(A) \(\frac{4}{6}\)
(B) \(\frac{2}{6}\)
(C) \(\frac{3}{8}\)
(D) \(\frac{1}{6}\)
Answer:
Question 9.
Multi-Step Paul needs to measure \(\frac{1}{4}\) cup lemon juice to make lemonade. how many times should he fill his \(\frac{1}{8}\)-cup measuring cup?
(A) four times
(B) three times
(C) two times
(D) eight times
Answer:
Question 10.
Multi-Step Carrie needs \(\frac{1}{3}\) cup of peanuts and \(\frac{1}{3}\) cup of walnuts for her trail mix. Which fraction is equivalent to the total amount of nuts Carrie needs for her mix?
(A) \(\frac{2}{6}\)
(B) \(\frac{3}{9}\)
(C) \(\frac{3}{6}\)
(D) \(\frac{6}{9}\)
Answer: