Refer to our Texas Go Math Grade 4 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 4 Lesson 14.5 Answer Key Unknown Angle Measures.
Texas Go Math Grade 4 Lesson 14.5 Answer Key Unknown Angle Measures
Essential Question
How can you use the strategy draw a diagram to solve angle measurement problems?
Answer:
Unlock the Problem
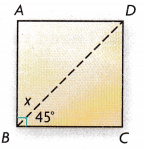
Mr. Tran is cutting a piece of kitchen tile as shown at the right. He needs tiles with 45° angles to make a design. After the cut, what is the angle measure of the part left over? Can Mr. Tran use both pieces in the design?
Answer:
The angle that measures the part left over is 45°. And Mr. Tran can use both pieces in the design.
Explanation:
Given that Mr. Tran needs tiles with 45° angles to make a design. So the angle that measures the part left over is
90° = 45°+X°
X° = 90°-45°
= 45°.
So, Mr. Tran use both pieces in the design.
Use the graphic organizer below to solve the problem.
Read
What do I need to find?
I need to find
Answer:
Here, we needed to find the angle that measures the part left over.
What information am I given?
I can use the measures of the angles I know.
Answer:
Given the information is the measurement of the tile which is 90°.
Plan
What is my plan or strategy?
I can draw a strip diagram and use the information to
Answer:
We have used subtraction to know the other angle measurement.
Solve
I can draw a strip diagram tõ represent the problem.
Then I can write an equation to solve the problem.
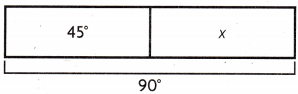
m∠ABD + m∠CBD = m∠ABC
x + ___________ = ___________
x = ___________
The m∠ABD = ___________ .
Since both tiles measure _________. Mr. Tran can use both pieces in the design.
Answer:
m∠ABD = 45°.
Mr. Tran can use both pieces in the design.
Explanation:
Given that the m∠ABC is 90° and the m∠ABD is 45° and the m∠CBD is X°. So the value of the X is
m∠ABC = m∠ABD + m∠CBD
90° = 45°+X°
90°-45° = X°
X° = 45°.
Since both tiles measure 45° and Mr. Tran can use both pieces in the design.
Math Talk
Mathematical Processes
What other equation can you write to solve the problem? Explain.
Answer:
The other equation can you write to solve the problem is 90°-45° = X°.
Try Another Problem
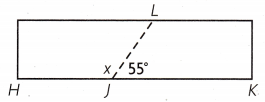
Marisol is building a frame for a sandbox, but the boards she has are too short. She must join two boards together to build a side as shown. At what angle did she cut the first board?
Answer:
Explanation:
Given that Marisol is building a frame for a sandbox, but the boards she has are too short. As the m∠HJK is 180° and the m∠LJK is 55° and m∠HJL is X°, so we need to find out the value of X. The equation will be
m∠HJK = m∠HJL+m∠LJK
180° = X°+55°
X° = 180° -55°
= 125°.
So Marisol cut the first board at 125°.
Read
What do I need to find?
Answer:
We need to find the angle that did she cut the first board.
What information am I given?
Answer:
Given that Marisol is building a frame for a sandbox,
Plan
What is my plan or strategy?
Answer:
We will perform subtraction to know the value of the X.
Solve
Explain how you can check the answer to the problem.
Answer:
We can check the answer by adding the value of the adding both the measurements of the angles.
Share and Show
Question 1.
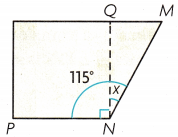
Laura cuts a square out of scrap paper as shown.
What is the angle measure of the piece left over?
First, draw a strip diagram to represent the problem.
Next, write the equation you need to solve.
Last, find the angle measure of the piece left over.
The m∠MNQ = _________ .
So, the angle measure of the piece left over is ____________ .
Answer:
The angle measure of the piece leftover is 25°.
Explanation:
Here, we can see a square out of scrap paper and we need to find out the angle measure of the piece leftover. So the strip of the diagram is
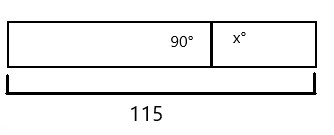
So the equation will be
115°-90° = X°
X° = 25°.
And the angle m∠MNQ will be 25°,
So, the angle measure of the piece leftover is 25°.
Question 2.
Apply Jackie trimmed a rectangular piece of scrap metal as shown. What is the measure of the unknown angle in the piece she trimmed off?
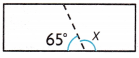
Answer:
Problem Solving
Question 3.

H.O.T. What if in Exercise 1, Laura cut a smaller square as shown? Would the m∠MNQ be different? Explain.
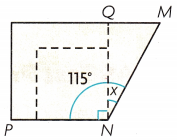
Answer:
No.
Explanation:
No, here the size of the square has changed but the angles are still the same.
Question 4.
H.O.T. Multi-Step The map shows Marco’s paper route. Marco turns right onto Center Street from Main Street. What is x, the measure of the angle formed by Main Street and Center Street?
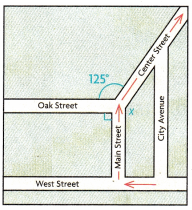
Answer:
The measure of the angle formed by Main Street and Center Street is 55°.
Explanation:
Given that Marco turns right onto Center Street from Main Street, where we need to know the value of the X which is the measure of the angle formed by Main Street and Center Street. So the equation will be
X°+125°+180° = 360°
X°+305° = 360°
X° = 360°-305°
= 55°.
Daily Assessment Task
Fill in the bubble completely to show your answer.
Question 5.
Austin cuts a triangle out of some scrap wood as shown. The angle measure of ∠XYZ is given. What is the angle measure of ∠XYIV?
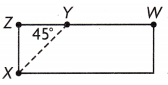
(A) 180°
(B) 125°
(C) 45°
(D) 135°
Answer:
D.
Explanation:
Given that Austin cuts a triangle out of some scrap wood and the angle measure of ∠XYZ is 45° and the measure of the ∠XYW is
∠XYW = 180°-45°
= 135°.
Question 6.
Shamika wants to cut a rectangle out of the piece of fabric shown. What is x, the angle measure of the piece of fabric that is left over?
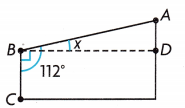
(A) 90°
(B) 22°
(C) 112°
(D) 68°
Answer:
B.
Explanation:
Given that Shamika wants to cut a rectangle out of the piece of fabric, so the measure of the piece of fabric that is leftover angle is
X° = 112°-90°
= 22°.
Question 7.
Multi-Step Evaluate Three angles form a straight angle. One angle measures 90°. Another angle measures 26°.
What is the measure of the third angle?
(A) 90°
(B) 26°
(C) 64°
(D) 154°
Answer:
C.
Explanation:
Given that three angles form a straight angle, one angle measures 90° and another angle measures 26°. So the measure of the third angle be X,
180° = X°+90°+26°
180° = X°+116°
X° = 180°-116°
= 64°.
TEXAS Test Prep
Question 8.
What is the measure of the unknown angle in the figure?
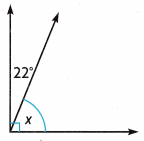
(A) 22°
(B) 68°
(C) 90°
(D) 158°
Answer:
B.
Explanation:
The measure of the unknown angle in the figure is
X° = 90°-22°
= 68°.
Texas Go Math Grade 4 Lesson 14.5 Homework and Practice Answer Key
Choose a method. Then find the product.
Question 1.
Anna Cut a square from a scrap to make a patch. What is the angle measure of the piece left over?
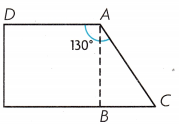
m ∠BAC = __________
Answer:
m ∠BAC = 40°.
Explanation:
Given that Anna Cut a square from scrap to make a patch and the measure of the piece leftover angle is
X° = 130°-90°
= 40°.
So m ∠BAC = 40°.
Question 2.
Pablo cut a tile at the angle shown. At what angle is the first piece cut?
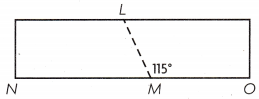
m ∠LMN = __________
Answer:
m ∠LMN = 65°..
Explanation:
Given that Pablo cut a tile at the angle and the first piece cut angle is
X° = 180°-115°
= 65°.
So m ∠LMN is 65°.
Question 3.
Cassie is cutting letters from rectangular sheets of paper. What is x, the measure of the angle of the piece she trimmed off?
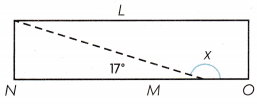
Answer:
X° = 163°.
Explanation:
Given that Cassie is cutting letters from rectangular sheets of paper and the measure of the angle of the piece she trimmed off is
X° = 180°-17°
= 163°.
Question 4.
Walt combined two pieces of tile to fit a corner in his room. What is the measure of ∠ECD?
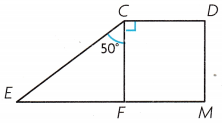
m∠ECD = _____________
Answer:
m∠ECD = 140°.
Explanation:
Given that Walt combined two pieces of tile to fit a corner in his room, so the measure of m∠ECD is
m∠ECD = 50°+90°
= 140°.
Problem Solving
Question 5.
Jaycee cut a square of fabric from a scrap. What is the angle measure of ∠MKJ?
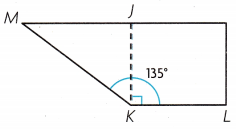
Answer:
∠MKJ = 45°.
Explanation:
Given that Jaycee cut a square of fabric from scrap, so the measure of ∠MKJ is
∠MKJ = 135°-90°
= 45°.
Question 6.
Mark cut a rectangular piece of wood at the angle shown. What is the measure of ∠SQP in the first piece cut?
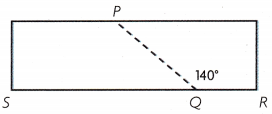
Answer:
∠SQP = 40°.
Explanation:
Given that Mark cut a rectangular piece of wood at the angle and the measure of ∠SQP in the first piece cut is
∠SQP = 180°-140°
= 40°.
Lesson Check
Fill in the bubble completely to show your answer.
Question 7.
What is the measure of the unknown angle ABD? Angle ABC is a right angle.
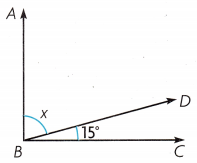
(A) 80°
(B) 105°
(C) 165°
(D) 75°
Answer:
D.
Explanation:
Given that ∠ABC is a right angle which is 90° and the measure of the unknown angle ABD is
X° = 90°-15°
= 75°.
Question 8.
Carol cut a triangle out of a rectangular tile to make a mosaic.
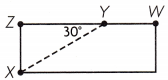
What is the measure of angle XYW in the piece leftover?
(A) 180°
(B) 45°
(C) 150°
(D) 60°
Answer:
D.
Explanation:
Given that Carol cut a triangle out of a rectangular tile to make a mosaic and the measure of angle XYW in the piece leftover is
∠XYW = 90°-30°
= 60°.
Question 9.
Jason wants to add a fence to his yard to make it the shape of a rectangle.
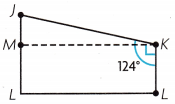
What is the measure of angle MKJ in the portion of the yard not inside the fence?
(A) 34°
(B) 146°
(C) 56°
(D) 90°
Answer:
A.
Explanation:
The measure of angle MKJ in the portion of the yard not inside the fence is
∠MKJ = 124°-90°
= 34°.
Question 10.
What is the measure of the unknown angle in the figure?
im – 21
(A) 90°
(B) 150°
(C) 60°
(D) 180°
Answer:
Question 11.
Multi-Step Two angles join to form a right angle. The measure of one of the angles is 64°. What is the measure of the other angle?
(A) 116°
(B) 26°
(C) 90°
(D) 36°
Answer:
B.
Explanation:
Given that the two angles join to form a right angle and the measure of one of the angles is 64°. So the measure of the other angle is 90°-64° which is 26°.
Question 12.
Multi-Step Three angles join to form a straight angle. One angle measures 45°. Another angle measures 50°. What is the measure of the third angle?
(A) 85°
(B) 95°
(C) 130°
(D) 100°
Answer:
A.
Explanation:
As the straight angle is 180° and given that one angle measures 45° and another angle measures 50°. So the measurement of two angles is 45°+50° which is 95°. So the value of the third angle is 180°-95° which is 85°.