Refer to our Texas Go Math Grade 4 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 4 Lesson 14.2 Answer Key Degrees.
Texas Go Math Grade 4 Lesson 14.2 Answer Key Degrees
Essential Question
How are degrees related to fractional parts of a circle?
Answer:
Connect You can use what you know about angles and fractional parts of a circle to understand angle measurement. Angles are measured in units called degrees. Think of a circle divided into 360 equal parts. An angle that cuts \(\frac{1}{360}\) out of the circle measures 1 degree(°).

Math Idea
An angle that cuts \(\frac{n}{360}\) out of a circle measures n degrees.
Unlock the Problem
The angle between two spokes on the bicycle wheel curs out or turns through \(\frac{10}{360}\) of a circle. What is the measure of the angle between the spokes?
Answer:
What part of an angle does a spoke represent?
Answer:
The Ray.
Explanation:
The part of an angle does a spoke represents is the ray that turns the side of an angle.
Example 1 Use fractional parts to find the angle measure.
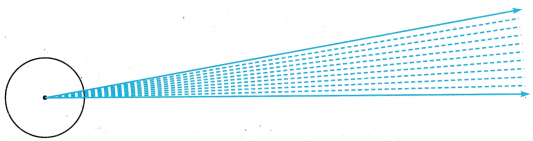
Each \(\frac{1}{360}\) turn measures ______________ degree.
Ten \(\frac{1}{360}\) turns measure ______________ degrees.
So, the measure of the angle between the spokes is ______________ .
Answer:
Each \(\frac{1}{360}\) turn measures 1 degree.
Ten \(\frac{1}{360}\) turns measure 10 degrees.
So, the measure of the angle between the spokes is 10 degrees.
Explanation:
Here, each \(\frac{1}{360}\) turn measures 1 degree and ten \(\frac{1}{360}\) turns measure 10 degrees. So, the measure of the angle between the spokes is 10 degrees.
Math Talk
Mathematical Processes
How many degrees is the measure of an angle that turns through 1 whole circle? Explain.
Answer:
360 degrees.
Explanation:
Here, an angle is measured with reference to a circle and with its center at the common endpoint of the rays. So the measure of an angle will be 360 degrees that turn through 1 whole circle.
Example 2 Find the measure of a right angle.

Remember: To write an equivalent fraction, multiply the numerator and denominator by the same factor.
STEP 1 Write \(\frac{1}{4}\) as an equivalent fraction with 360 in the denominator.
\(\frac{1}{4}\) = \(\frac{}{360}\) Think: 4 × 9 = 36, so 4 × __________ = 360.
Answer:
The equivalent fraction is \(\frac{90}{360}\).
Explanation:
Here, \(\frac{1}{4}\) fraction of a circle does a right angle cut out. And the \(\frac{1}{4}\) as an equivalent fraction with 360 in the denominator is
\(\frac{1}{4}\) = \(\frac{90}{360}\).
STEP 2 Write \(\frac{90}{360}\) in degrees.
An angle that cuts \(\frac{1}{360}\) out of a circle measures __________ .
An angle that cuts out \(\frac{90}{360}\) of a circle measures __________ .
So, a right angle measures __________ .
Answer:
An angle that cuts \(\frac{1}{360}\) out of a circle measures 1 degree.
An angle that cuts out \(\frac{90}{360}\) of a circle measures 90 degrees.
So, a right angle measures 90 degrees.
Explanation:
Here, an angle that cuts \(\frac{1}{360}\) out of a circle measures is 1 degree and an angle that cuts out \(\frac{90}{360}\) of a circle measures is 90 degrees. So, a right angle measure is 90 degrees.
Share and Show
Question 1.
Find the measure of the angle.
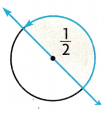
What fraction of the circle does the angle cut out? ______________
\(\frac{1}{2}\) = \(\frac{}{360}\) Think: 2 × 18 = 36, so 2 × __________ = 360.
So, the measure of the angle is ___________ .
Answer:
Tell the measure of the angle in degrees.
Question 2.
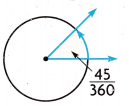
Answer:
45 degrees.
Explanation:
The measure of the angle in degrees is 45 degrees.
Question 3.
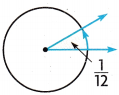
Answer:
The measure of the angle is 30 degrees.
Explanation:
The measure of the angle in degrees is, here we will multiply both numerator and denominator with 30. So the measure of the angle will be \(\frac{1}{12}\) × \(\frac{30}{30}\) then it will be \(\frac{30}{360}\). So the measure of the angle is 30 degrees.
Math Talk
Mathematical Processes
If an angle measures 60°, what fraction of a circle does it cut out? Explain.
Answer:
Unlock the Problem
Question 4.

H.O.T. Multi-Step Ava started reading at 3:30 P.M. She stopped for a snack at 3:50 P.M. During this time, through what fraction of a circle did the minute hand turn? How many degrees did the minute hand turn?

Answer:
The of a circle did the minute hand turn is latex]\frac{5}{6}[/latex] turn.
Explanation:
Given that Ava started reading at 3:30 P.M and she stopped for a snack at 3:50 P.M. So the fraction of a circle did the minute hand turn is latex]\frac{5}{6}[/latex] turn and the degrees did the minute hand turns is 185 degrees.
a. What are you asked to find?
Answer:
Asked to find the fraction of a circle did the minute hand turns and how many degrees did the minute hand turn.
b. What information can you use to find the fraction of a circle through which the minute hand turned?
Answer:
Here, the given information is 3:30 P.M to 3:50 P.M 20 minutes elapsed.
c. How can you use the fraction of a circle through which the minute hand turned to find how many degrees it turned?
Answer:
The fraction of a circle did the minute hand turn is latex]\frac{5}{6}[/latex] turn and the degrees did the minute hand turns is 185 degrees.
d. Show how to solve the problem.
![]()
Answer:
\(\frac{(1×120)}{(3×120)}\) = \(\frac{(120)}{(360)}\).
Explanation:
Here, we will multiply both numerator and denominator with 120 then it will be
\(\frac{(1×120)}{(3×120)}\) = \(\frac{(120)}{(360)}\).
e. Complete the sentences.
From 3:30 P.M. to 3:50 P.M., the minute hand made a ______ turn clockwise.
The minute hand turned ___________ degrees.
Answer:
From 3:30 P.M. to 3:50 P.M., the minute hand made a \(\frac{5}{6}\) turn clockwise.
The minute hand turned 185 degrees.
Explanation:
The fraction of a circle did the minute hand turn is \(\frac{5}{6}\) turn and the degrees did the minute hand turns is 185 degrees.
Question 5.
H.O.T. write Math
Is this angle measure obtuse? Explain.

Answer:
No.
Explanation:
No, as the angle is greater than 180 degrees.
Question 6.
Analyze What fraction of a circle does a straight angle cut out? What is the measure of a straight angle? Explain.
Answer:
Daily Assessment Task
Fill in the bubble completely to show your answer.
Question 7.
What is the measure of the angle in degrees?
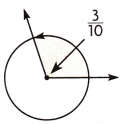
(A) 108°
(B) 95°
(C) 95°
(D) 90°
Answer:
A.
Explanation:
The measure of the angle in degrees is \(\frac{3}{10}\) × \(\frac{36}{36}\) which is 108 degrees.
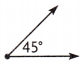
Question 8.
Use Mathematical Language What type of angle is shown?
(A) right
(B) obtuse
(C) acute
(D) straight
Answer:
C.
Explanation:
Here, 45 degrees is an acute angle as it is half of the right angle.
Question 9.
Multi-Step A circle is divided into 8 equal sections. An angle measures the same as the total measure of 3 of the sections. What is the measure of the angle?
(A) 270°
(B) 90°
(C) 45°
(D) 135°
Answer:
D.
Explanation:
As one revolution of the circle is 360 degrees and here the circle is divided into 8 equal sections which is 360÷8 = 45 degrees. So the measure of the angle is 45×3 which is 135 degrees.
TEXAS Test Prep
Question 10.
How many degrees are in an angle that cuts of a circle?
(A) 90°
(B) 180°
(C) 270°
(D) 360°
Answer:
D.
Explanation:
360 degrees are at an angle that cuts of a circle.
Texas Go Math Grade 4 Lesson 14.2 Homework and Practice Answer Key
Question 1.
Find the measure of the angle.
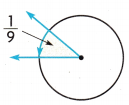
What fraction of the circle does the angle cut out? ___________
\(\frac{1}{9}\) = \(\frac{}{360}\)
So, the measure of the angle is ______________.
Answer:
The fraction of the circle does the angle cut out is \(\frac{1}{9}\).
An angle that cuts out \(\frac{40}{360}\) of a circle measures 40 degrees.
So, a right angle measures 40 degrees.
Explanation:
Here the fraction of the circle does the angle cut out is \(\frac{1}{9}\) and the angle that cuts out \(\frac{40}{360}\) of a circle measures 40 degrees.
Tell the measure of the angle in degrees.
Question 2.
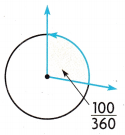
Answer:
10 degrees.
Explanation:
The measure of the angle in degrees is 10 degrees.
Question 3.
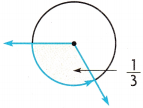
Answer:
120 degrees.
Explanation:
The measure of the angle in degrees is \(\frac{1}{3}\) × \(\frac{120}{120}\) which is \(\frac{120}{360}\). So the angle is 120 degrees.
Problem Solving
Question 4.
At 6:10 P.M., Elena left her house to walk to Claire’s house. She arrived at 6:25 P.M. During this time, through what fraction of a circle did the minute hand turn?

Answer:
\(\frac{5}{12}\).
Explanation:
Given that at 6:10 P.M. Elena left her house to walk to Claire’s house and she arrived at 6:25 P.M, so the fraction of a circle did the minute hand turn is \(\frac{5}{12}\).
Question 5.
How many degrees did the minute hand turn as it moved from 2 to 5?
Answer:
The total angle in between 2 and 5 is 90 degrees.
Explanation:
As a clock has 12 partitions in hours and 60 partitions in minute and the total angle of a clock is 360 degrees i.e. 12 hours which is 60 degrees = 360 degrees. So for 1 minute = \(\frac{360}{60}\) which is 6 degrees. And now from 2-5 there are total 15 minutes in between. So the total angle in between 2 and 5 is 15×6 which is 90 degrees.
Question 6.
Suppose Elena takes a route that is 15 minutes longer. How would this change your answers to exercises 4 and 5? Explain.
Answer:
Lesson Check
Fill In the bubble completely to show your answer.
Question 7.
Which type of angle is shown?
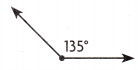
(A) acute
(B) straight
(C) obtuse
(D) right
Answer:
C.
Explanation:
As the angle is greater than the right angle and less than 180 degrees.
Question 8.
What is the measure of the angle in degrees?

(A) 45°
(B) 72°
(C) 2°
(D) 90°
Answer:
B.
Explanation:
The measure of the angle in degree is \(\frac{2}{10}\) × \(\frac{36}{36}\) which is \(\frac{72}{360}\). So the angle is 72 degree.
Question 9.
How many degrees are in an angle that cuts \(\frac{2}{5}\) of a circle?
(A) 144°
(B) 30°
(C) 180°
(D) 50°
Answer:
A.
Explanation:
The measure of the angle in degree is \(\frac{2}{5}\) × \(\frac{72}{72}\) which is \(\frac{144}{360}\). So the angle is 144 degree.
Question 10.
What is the measure of the angle in degrees?
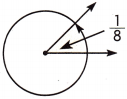
(A) 80°
(B) 90°
(C) 35°
(D) 45°
Answer:
D.
Explanation:
The measure of the angle in degree is \(\frac{1}{8}\) × \(\frac{45}{45}\) which is \(\frac{45}{360}\). So the angle is 45 degree.
Question 11.
Multi-Step Alex cut a pizza into 8 equal slices. He removed 2 of the slices of pizza. What is the measure of the angle made by the missing slices of pizza?
(A) 45°
(B) 20°
(C) 90°
(D) 80°
Answer:
A.
Explanation:
Given that Alex cut a pizza into 8 equal slices and he removed 2 of the slices of pizza. So the measure of the angle made by the missing slices of pizza is, as one revolution of the circle is 360 degrees and here the circle is divided into 8 equal sections which is 360÷8 = 45 degrees. So the measure of the angle made by the missing slices of pizza is \(\frac{1}{8}\) × \(\frac{45}{45}\) which is 45 degrees.
Question 12.
Multi-Step Julia woke up at 7:05 A.M. She left for school at 7:25 A.M. How many degrees did the minute hand on the clock turn from the time Julia woke up to the time she left for school?
(A) 120°
(B) 60°
(C) 180°
(D) 90°
Answer: