Refer to our Texas Go Math Grade 4 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 4 Lesson 1.1 Answer Key Place Value and Pattern.
Texas Go Math Grade 4 Lesson 1.1 Answer Key Place Value and Patterns
Investigate
Materials base-ten blocks
You can use base-ten blocks to understand the relationships among place-value positions. Use a large cube for 1,000, a flat for 100, along with the cube for 10, and a small cube for 1.
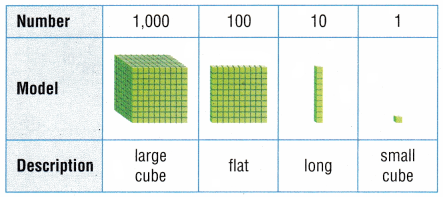
Complete the comparisons below to describe the relationship from one place-value position to the next place-value position.
A.
Look at the long and compare it to the small cube.
The long is ________ times as much as the small cube.
Answer:
The given table is:

Now,
From the given table,
We can observe that
The length is 10 times as much as the small cube.
Hence, from the above,
We can conclude that
The length is 10 times as much as the small cube.
Look at the flat and compare it to the long.
The flat is _________ times as much as the long.
Answer:
The given table is:

Now,
From the given table,
We can observe that
The flat is 10 times as much as the long.
Hence, from the above,
We can conclude that
The flat is 10 times as much as the long.
Look at the large cube and compare it to the flat.
The large cube is ___________ times as much as the flat.
Answer:
The given table is:

Now,
From the given table,
We can observe that
The large cube is 10 times as much as the flat.
Hence, from the above,
We can conclude that
The large cube is 10 times as much as the flat.
B.
Look at the flat and compare it to the large cube.
The flat is ___________ of the large cube.
Answer:
The given table is:

Now,
From the given table,
We can observe that
The flat is \(\frac{1}{10}\) of the large cube.
Hence, from the above,
We can conclude that
The flat is \(\frac{1}{10}\) of the large cube.
Look at the long and compare it to the flat.
The long is ___________ of the flat.
Answer:
The given table is:

Now,
From the given table,
We can observe that
The long is \(\frac{1}{10}\) of the flat.
Hence, from the above,
We can conclude that
The long is \(\frac{1}{10}\) of the flat.
Look at the small cube and compare it to the long.
The small cube is ___________ of the long.
Answer:
The given table is:

Now,
From the given table,
We can observe that
The small cube is \(\frac{1}{10}\) of the long.
Hence, from the above,
We can conclude that
The small cube is \(\frac{1}{10}\) of the long.
Make Connections
You can use your understanding of place-value patterns and a place-value chart to write numbers that are 10 times as much as or \(\frac{1}{10}\) of any given number.

3,000 is 10 times as much as 300.
30 is \(\frac{1}{10}\) of 300.
Use the steps below to complete the below table.
STEP 1. Write the given number in a place-value chart.
STEP 2. Use the place-value chart to write a number that is 10 times as much as the given number.
STEP 3. Use the place-value chart to write a number that is of the given number.

Answer:
The given steps are:
STEP 1. Write the given number in a place-value chart.
STEP 2. Use the place-value chart to write a number that is 10 times as much as the given number.
STEP 3. Use the place-value chart to write a number that is of the given number.
Hence, from the above,
We can conclude that
The complete table by using the given steps is:

Share and Show
Complete the sentences.
Question 1.
500 is 10 times as much as ____________ .
Answer:
We know that,
If a number x is as many times as much as the same number and the result is represented as y, then the representation of that operation is:
x × a = y
If a number y is \(\frac{1}{a}\) the same number and the result is represented as x, then the representation of that operation is:
y × \(\frac{1}{a}\) = x
So,
According to the above definition,
x × 10 = 500
x = \(\frac{500}{10}\)
x = 50
Hence, from the above,
We can conclude that
500 is 10 times as much as 50
Question 2.
20,000 is \(\frac{1}{10}\) of ____________ .
Answer:
We know that,
If a number x is as many times as much as the same number and the result is represented as y, then the representation of that operation is:
x × a = y
If a number y is \(\frac{1}{a}\) the same number and the result is represented as x, then the representation of that operation is:
y × \(\frac{1}{a}\) = x
So,
According to the above definition,
x = 20,000 × \(\frac{1}{10}\)
x = 2,000
Hence, from the above,
We can conclude that
20,000 is \(\frac{1}{10}\) of 2,000
Use the place-value patterns to complete the table.

Answer:
We know that,
If a number x is as many times as much as the same number and the result is represented as y, then the representation of that operation is:
x × a = y
If a number y is \(\frac{1}{a}\) the same number and the result is represented as x, then the representation of that operation is:
y × \(\frac{1}{a}\) = x
Hence, from the above,
We can conclude that
The complete table is:
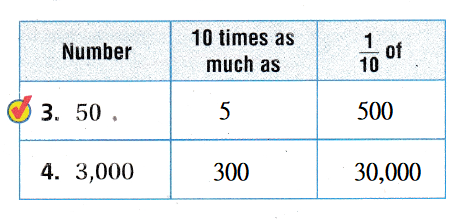

Answer:
We know that,
If a number x is as many times as much as the same number and the result is represented as y, then the representation of that operation is:
x × a = y
If a number y is \(\frac{1}{a}\) the same number and the result is represented as x, then the representation of that operation is:
y × \(\frac{1}{a}\) = x
Hence, from the above,
We can conclude that
The complete table is:

Complete the sentence with 100 or 1,000
Question 7.
200 is _______________ times as much as 2.
Answer:
We know that,
If a number x is as many times as much as the same number and the result is represented as y, then the representation of that operation is:
x × a = y
If a number y is \(\frac{1}{a}\) the same number and the result is represented as x, then the representation of that operation is:
y × \(\frac{1}{a}\) = x
So,
According to the above,
2 × a = 200
a = \(\frac{200}{2}\)
a = 100
Hence, from the above,
We can conclude that
200 is 100 times as much as 2.
Question 8.
7,00,000 is ___________ times as much as 700.
Answer:
We know that,
If a number x is as many times as much as the same number and the result is represented as y, then the representation of that operation is:
x × a = y
If a number y is \(\frac{1}{a}\) the same number and the result is represented as x, then the representation of that operation is:
y × \(\frac{1}{a}\) = x
So,
According to the above,
700 × a = 700,000
a = \(\frac{700,000}{700}\)
a = 1,000
Hence, from the above,
We can conclude that
7,00,000 is 1,000 times as much as 700.
Question 9.
4,000 is ___________ times as much as 4.
Answer:
We know that,
If a number x is as many times as much as the same number and the result is represented as y, then the representation of that operation is:
x × a = y
If a number y is \(\frac{1}{a}\) the same number and the result is represented as x, then the representation of that operation is:
y × \(\frac{1}{a}\) = x
So,
According to the above,
4 × a = 4,000
a = \(\frac{4,000}{4}\)
a = 1,000
Hence, from the above,
We can conclude that
4,000 is 1,000 times as much as 4.
Question 10.
600 is _____________ times as much as 6.
Answer:
We know that,
If a number x is as many times as much as the same number and the result is represented as y, then the representation of that operation is:
x × a = y
If a number y is \(\frac{1}{a}\) the same number and the result is represented as x, then the representation of that operation is:
y × \(\frac{1}{a}\) = x
So,
According to the above,
6 × a = 600
a = \(\frac{600}{6}\)
a = 100
Hence, from the above,
We can conclude that
600 is 100 times as much as 6.
Problem Solving
Question 11.
Mark and Robyn used base-ten blocks to show that 300 in 100 times as much as 3. Whose model makes sense? Whose model is nonsense? Explain your reasoning.
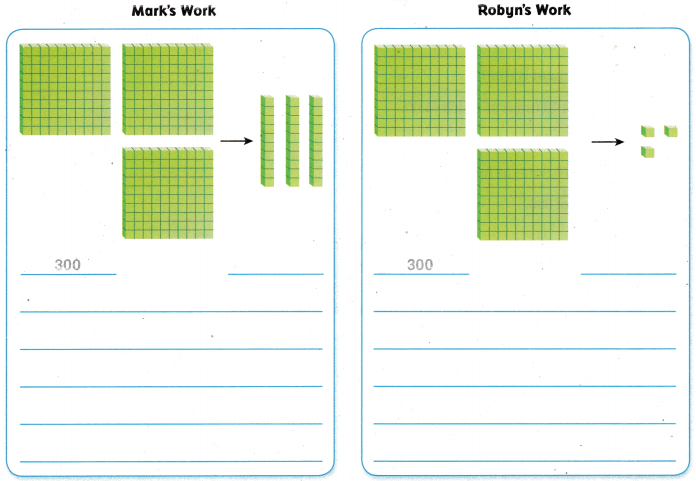
Answer:
It is given that
Mark and Robyn used base-ten blocks to show that 300 in 100 times as much as 3
Now,
We know that,
If a number x is as many times as much as the same number and the result is represented as y, then the representation of that operation is:
x × a = y
Now,
According to the given information,
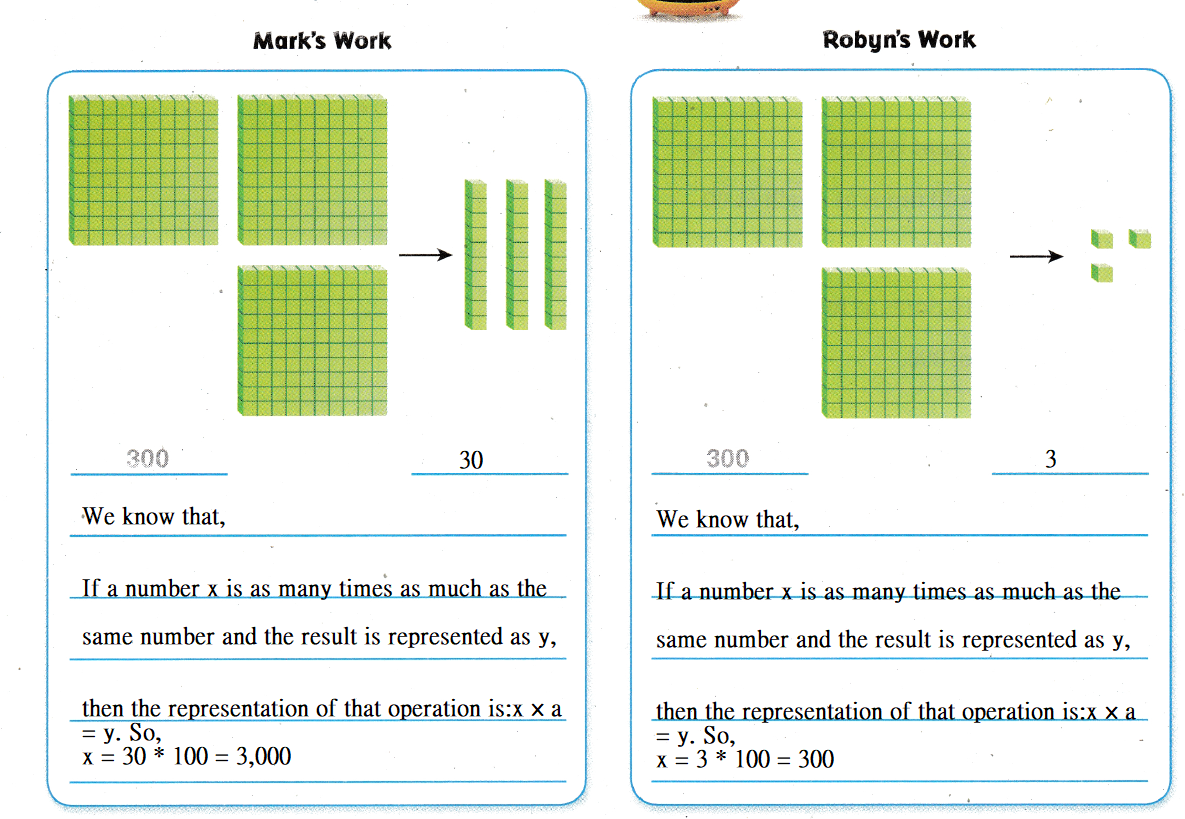
Hence, from the above,
We can conclude that
Mark’s model is nonsense
Question 12.
Explain How you would help Mark understand why he should have used small cubes instead of longs.
Answer:
We know that,
We know that,
If a number x is as many times as much as the same number and the result is represented as y, then the representation of that operation is:
x × a = y
So,
We considered “Cubes” as 1 unit
We considered “Longs” as a combination of “10 cubes” i.e., 10 units
Hence, from the above,
We can conclude that
Since Mark’s model has a single digit, he considered using “Cubes”
Daily Assessment Task
Fill in the bubble completely to show your answer.
Question 13.
Melinda has 500 pennies in a jar. Brenda has 10 times as many pennies as Melinda does. How many pennies does Brenda have?
A. 50,000
B. 5
C. 5,000
D. 50
Answer:
It is given that
Melinda has 500 pennies in a jar. Brenda has 10 times as many pennies as Melinda does
Now,
We know that,
If a number x is as many times as much as the same number and the result is represented as y, then the representation of that operation is:
x × a = y
If a number y is \(\frac{1}{a}\) the same number and the result is represented as x, then the representation of that operation is:
y × \(\frac{1}{a}\) = x
Now,
Let the number of pennies Brenda has to be: y
Now,
According to the given information,
y = 500 × 10
= 5,000 pennies
Hence, from the above,
We can conclude that
The number of pennies does Brenda have is:

Question 14.
Which statement is true?
A. 8,000 is 10 times as much as 80.
B. 80 is \(\frac{1}{10}\) of 8.
C. 800 is 10 times as much as 80.
D. 8 is \(\frac{1}{10}\) of 800.
Answer:
We know that,
If a number x is as many times as much as the same number and the result is represented as y, then the representation of that operation is:
x × a = y
If a number y is \(\frac{1}{a}\) the same number and the result is represented as x, then the representation of that operation is:
y × \(\frac{1}{a}\) = x
Hence, from the above,
We can conclude that
The statement that is true is:
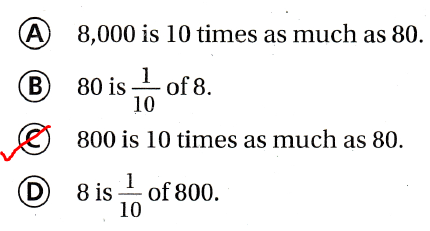
Question 15.
Multi-Step Harry has a collection of comic books. He currently has 1,000 comic books. His friend George has \(\frac{1}{10}\) the number of comic books that Harry does. Mike has \(\frac{1}{10}\) the number of comic books that George has. How many comic books does Mike have?
A. 1000
B. 100
C. 10,000
D. 10
Answer:
It is given that
Harry has a collection of comic books. He currently has 1,000 comic books. His friend George has \(\frac{1}{10}\) the number of comic books that Harry does. Mike has \(\frac{1}{10}\) the number of comic books that George has
Now,
Let y be the number of comic books George has
Let z be the number of comic books Mike has
Now,
We know that,
If a number x is as many times as much as the same number and the result is represented as y, then the representation of that operation is:
x × a = y
If a number y is \(\frac{1}{a}\) the same number and the result is represented as x, then the representation of that operation is:
y × \(\frac{1}{a}\) = x
So,
According to the given information,
The number of books George has = \(\frac{1,000}{10}\)
= 100 comic books
The number of books Mike has = \(\frac{100}{10}\)
= 10 comic books
Hence, from the above,
We can conclude that
The number of books Mike has:

Texas Test Prep
Question 16.
Sam has 1,300 dimes. Anna has \(\frac{1}{10}\) the number of dimes that Sam does. How many dimes does Anna have?
A. 13,000
B. 130
C. 13
D. 3
Answer:
It is given that
Sam has 1,300 dimes. Anna has \(\frac{1}{10}\) the number of dimes that Sam does
Now,
We know that,
If a number x is as many times as much as the same number and the result is represented as y, then the representation of that operation is:
x × a = y
If a number y is \(\frac{1}{a}\) the same number and the result is represented as x, then the representation of that operation is:
y × \(\frac{1}{a}\) = x
So,
According to the given information,
The number of dimes does Anna have = \(\frac{1,300}{10}\)
= 130 dimes
Hence, from the above,
We can conclude that
The number of dimes does Anna have:

Texas Go Math Grade 4 Lesson 1.1 Homework and Practice Answer Key
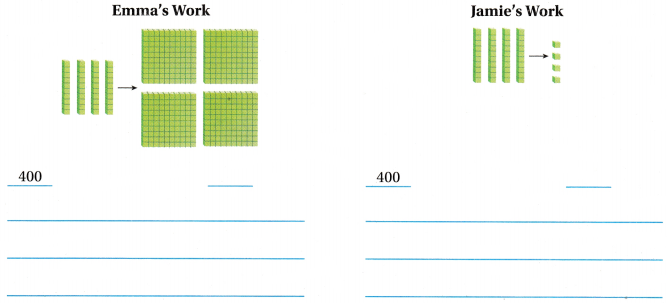
Question 1.
Emma and Jamie used base-ten blocks to show that 40 is one-tenth of 400. Whose model makes sense? Whose model is nonsense? Explain your reasoning.
Describe the relationship between the value of a dollar and the value of a dime.
Answer:
It is given that
Emma and Jamie used base-ten blocks to show that 40 is one-tenth of 400
Now,
We know that,
If a number x is as many times as much as the same number and the result is represented as y, then the representation of that operation is:
x × a = y
Now,
According to the given information,
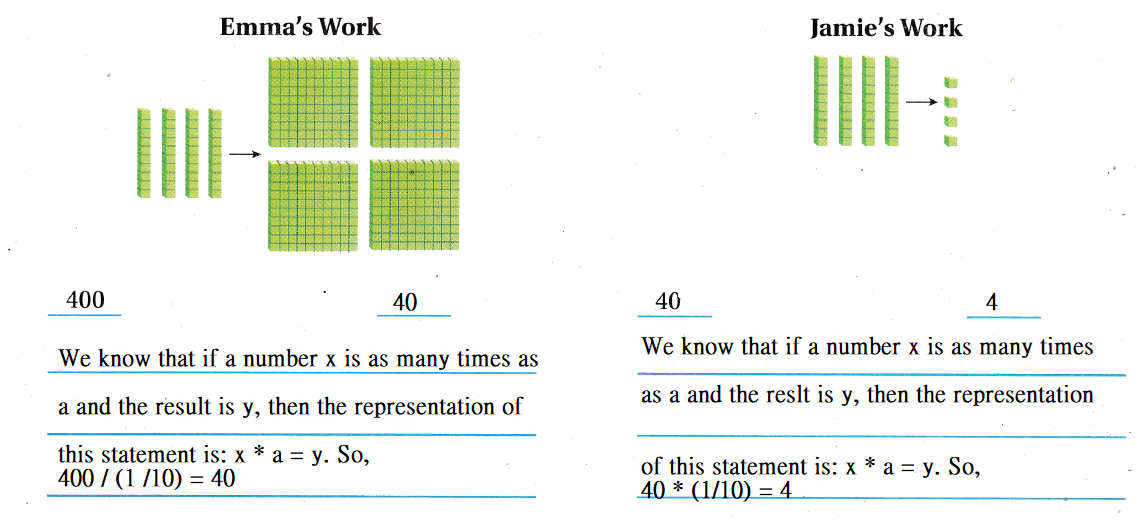
Hence, from the above,
We can conclude that
Emma’s model makes sense
Jamie’s model is nonsense
Problem Solving
Question 2.
Lisa had 3 dollars. She went to the bank and exchanged the 3 dollars for 30 dimes.
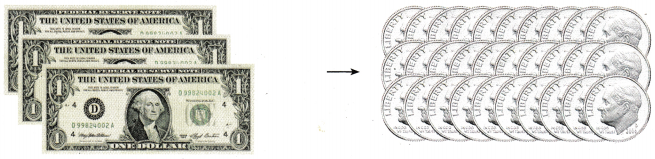
Describe the relationship between the value of a dollar and the value of a dime.
Answer:
It is given that
Lisa had 3 dollars. She went to the bank and exchanged the 3 dollars for 30 dimes.
Now,
We know that,
1 dollar = 10 dimes
So,
3 dollars = 30 dimes
Now,
We know that,
If a number x is as many times as much as the same number and the result is represented as y, then the representation of that operation is:
x × a = y
So,
According to the above information,
(The number of dimes) × 10 = (The number of dollars)
So,
The dollar is 10 times as many as 1 dimes
Hence, from the above,
We can conclude that
The relationship between the value of a dollar and the value of a dime is:
1 dollar = 10 dimes
Lesson Check
Fill in the bubble completely to show your answer.
Question 3.
Which statement is true?
A. 500 is 10 times as much as 50.
B. 500 is \(\frac{1}{10}\) much as 50.
C. 50,000 is 1,000 times as much as 5.
D. 5 is \(\frac{1}{10}\) as much as 500.
Answer:
We know that,
If a number x is as many times as much as the same number and the result is represented as y, then the representation of that operation is:
x × a = y
If a number y is \(\frac{1}{a}\) the same number and the result is represented as x, then the representation of that operation is:
y × \(\frac{1}{a}\) = x
Hence, from the above,
We can conclude that
The statement that is true is:
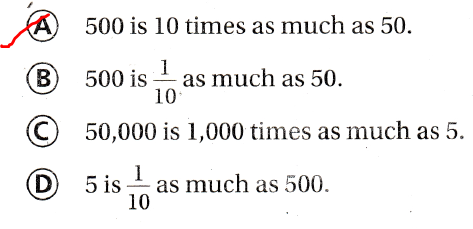
Question 4.
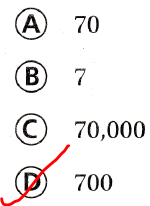
7,000 is ten times as much as what number?
A. 70
B. 7
C. 70,000
D. 700
Answer:
We know that,
If a number x is as many times as much as the same number and the result is represented as y, then the representation of that operation is:
x × a = y
If a number y is \(\frac{1}{a}\) the same number and the result is represented as x, then the representation of that operation is:
y × \(\frac{1}{a}\) = x
So,
According to the above statements,
x × 10 = 7,000
x = \(\frac{7,000}{10}\)
x = 700
Hence, from the above,
We can conclude that
7,000 is ten times as much as:
Question 5.
Which statement is true?
A. 90 is \(\frac{1}{10}\) of 100.
B. 900 is 100 times as much as 9.
C. 9,000 is 1,000 times as much as 90.
D. 9 is \(\frac{1}{10}\) of 900.
Answer:
We know that,
If a number x is as many times as much as the same number and the result is represented as y, then the representation of that operation is:
x × a = y
If a number y is \(\frac{1}{a}\) the same number and the result is represented as x, then the representation of that operation is:
y × \(\frac{1}{a}\) = x
Hence, from the above,
We can conclude that
The statement that is true is:
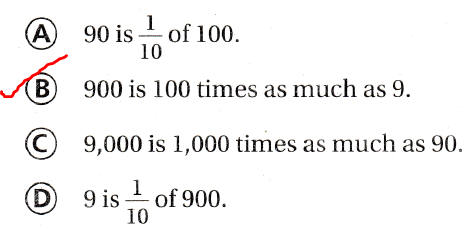
Question 6.
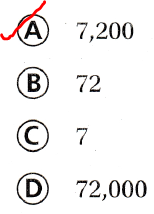
720 is \(\frac{1}{10}\) of what number?
A. 7,200
B. 72
C. 7
D. 72,000
Answer:
We know that,
If a number y is \(\frac{1}{a}\) the same number and the result is represented as x, then the representation of that operation is:
y × \(\frac{1}{a}\) = x
So,
According to the given information,
y ×\(\frac{1}{10}\) = 720
y = 720 × 10
y = 7,200
Hence, from the above,
We can conclude that
720 is \(\frac{1}{10}\) of:
Question 7.
Multi-Step The owner of Pattie’s Party Shop ordered 4 cartons of balloons. How many balloons did she order?

1 carton = 10 boxes
1 box = 10 packages
1 packages = 10 balloons
A. 40
B. 400
C. 40,000
D. 4,000
Answer:
It is given that
The owner of Pattie’s Party Shop ordered 4 cartons of balloons
Now,
We know that,
1 carton = 10 boxes
1 box = 10 packages
1 packages = 10 balloons
So,
The number of balloons did Pattie ordered = 4 × 10 boxes
= 4 × 10 × 10 packages
= 4 × 10 × 10 × 10 balloons
= 4 × 1,000
= 4,000 balloons
Hence, from the above,
We can conclude that
The number of balloons did Pattie ordered is:

Question 8.
Multi-Step Greg bought 2 boxes of balloons. He used half of them to decorate his yard. He used 40 to decorate his porch. He used the rest inside his house. How many balloons did he use inside?
A. 6
B. 6,000
C. 60
D. 600
Answer:
It is given that
Greg bought 2 boxes of balloons. He used half of them to decorate his yard. He used 40 to decorate his porch. He used the rest inside his house
Now,
We know that,
1 carton = 10 boxes
1 box = 10 packages
1 packages = 10 balloons
So,
The total number of balloons did Greg bought = 2 × 10 packages
= 2 × 10 × 10 balloons
= 200 balloons
So,
The number of balloons Greg used inside = 200 – (\(\frac{200}{2}\) + 40)
= 200 – 140
= 60 balloons
Hence, from the above,
We can conclude that
The number of balloons did Greg used inside is:
