Refer to our Texas Go Math Grade 3 Answer Key Pdf to score good marks in the exams. Test yourself by practicing the problems from Texas Go Math Grade 3 Lesson 3.2 Answer Key Compare Fractions with the Same Numerator.
Texas Go Math Grade 3 Lesson 3.2 Answer Key Compare Fractions with the Same Numerator
Essential Question
How can you compare fractions with the same numerator?
Answer:
To compare fractions with the same numerator, all you have to do is compare the denominators. The fraction with the bigger denominator is smaller.
Unlock the Problem
Josh is at Enzo’s Pizza Palace. He can sit at a table with 5 of his friends or at a different table with 7 of his friends. The same-size pizza is shared equally among the people at each table. At which table should Josh sit to get more pizza?
• Including Josh, how many friends will be sharing a pizza at each table?
Answer:
It is given that
Josh is at Enzo’s Pizza Palace. He can sit at a table with 5 of his friends or at a different table with 7 of his friends
Hence, from the above,
We can conclude that
The number of friends that will be sharing a pizza at each table including Josh is: 6 friends (or) 8 friends
• What will you compare?
Answer:
We will compare the total number of pieces that are shared by all the friends since all the friends will get only 1 piece
Model the problem.
There will be 6 friends sharing Pizza A or 8 friends sharing Pizza B.
So, Josh will get either \(\frac{1}{6}\) or \(\frac{1}{8}\) of a pizza.
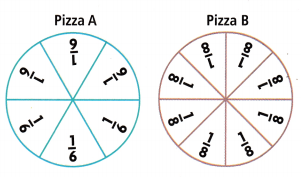
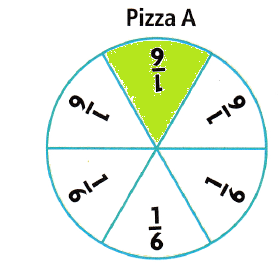
- Shade \(\frac{1}{6}\) of Pizza A.
- Shade \(\frac{1}{8}\) of Pizza B
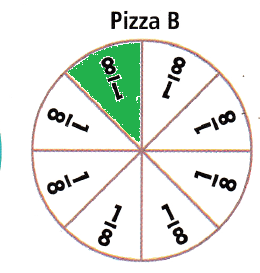 .
. - Which piece of pizza is larger?
- Compare the shaded parts.
\(\frac{1}{6}\) > \(\frac{1}{8}\)
So,
Josh should sit at the table with 6 friends to get more pizza.
Math talk
Mathematical Processes
Suppose Josh wants two pieces of one of the pizzas above. Is \(\frac{2}{6}\) or \(\frac{2}{8}\) of the pizza a greater amount? Explain how you know.
Answer:
It is given that
Josh wants two pieces of one of the pizzas.
The given two pieces of pizza are:
\(\frac{2}{6}\) and \(\frac{2}{8}\)
Now,
From the above fractions,
We can observe that
The numerators are the same
The fraction with the biggest denominator is smaller
So,
\(\frac{2}{6}\) > \(\frac{2}{8}\)
Hence, from the above,
We can conclude that
The \(\frac{2}{6}\) of the pizza has a greater amount
Question 1.
Which pizza has more pieces? ____
The more pieces a whole is divided into, ___ the pieces are.
Answer:
The given two pieces of pizza are:
\(\frac{2}{6}\) and \(\frac{2}{8}\)
Now,
From the above fractions,
We can observe that
The numerators are the same
The fraction with the biggest denominator is smaller
So,
\(\frac{2}{6}\) > \(\frac{2}{8}\)
Hence, from the above,
We can conclude that
The pizza that has 8 pieces has more pieces
The more pieces a whole is divided into, the greater the pieces are.
Question 2.
Which pizza has fewer pieces? ___
The fewer pieces a whole is divided into, the __ the pieces are.
Answer:
The given two pieces of pizza are:
\(\frac{2}{6}\) and \(\frac{2}{8}\)
Now,
From the above fractions,
We can observe that
The numerators are the same
The fraction with the biggest denominator is smaller
So,
\(\frac{2}{6}\) > \(\frac{2}{8}\)
Hence, from the above,
We can conclude that
The pizza that has 6 pieces has fewer pieces
The fewer pieces a whole is divided into, the lesser the pieces are.
Use fraction strips.
On Saturday, the campers paddled \(\frac{2}{8}\) of their planned route down the river. On Sunday, they paddled \(\frac{2}{3}\) of their route down the river. On which day did the campers paddle farther?
Compare \(\frac{2}{8}\) and \(\frac{2}{3}\).
- Place a ✓next to the fraction strips that show more parts in the whole.
- Shade \(\frac{2}{8}\). Then shade \(\frac{2}{3}\).
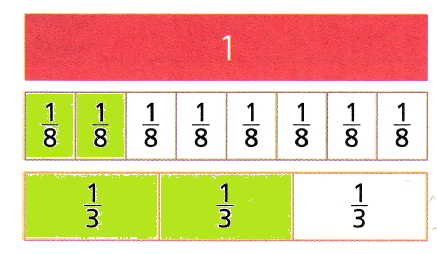
Compare the shaded parts.
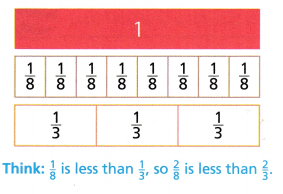
- So,
\(\frac{2}{8}\) < \(\frac{2}{3}\)
So,
The campers paddled farther on Sunday
Share and Show
Question 1.
Shade the models to show \(\frac{1}{6}\) and \(\frac{1}{4}\). Then compare the fractions.
\(\frac{1}{6}\) ![]() \(\frac{1}{4}\)
\(\frac{1}{4}\)
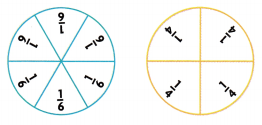
Answer:
The given fractions are:
\(\frac{1}{6}\) and \(\frac{1}{4}\)
So,
The representation of the given fractions are:
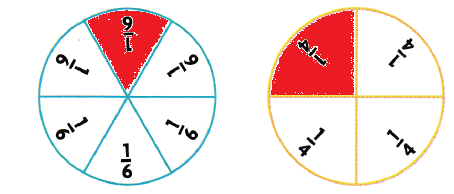
Now,
We know that,
The fraction with the bigger denominator is smaller.
Hence, from the above,
We can conclude that
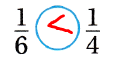
Compare. Write <, >, or .
Question 2.
\(\frac{1}{8}\) ![]() \(\frac{1}{3}\)
\(\frac{1}{3}\)
Answer:
The given fractions are:
\(\frac{1}{8}\) and \(\frac{1}{3}\)
Now,
We know that,
The fraction with the bigger denominator is smaller.
Hence, from the above,
We can conclude that
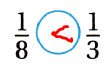
Question 3.
\(\frac{3}{4}\) ![]() \(\frac{3}{8}\)
\(\frac{3}{8}\)
Answer:
The given fractions are:
\(\frac{3}{4}\) and \(\frac{3}{8}\)
Now,
We know that,
The fraction with the bigger denominator is smaller.
Hence, from the above,
We can conclude that
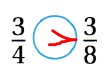
Question 4.
\(\frac{2}{6}\) ![]() \(\frac{2}{3}\)
\(\frac{2}{3}\)
Answer:
The given fractions are:
\(\frac{2}{6}\) and \(\frac{2}{3}\)
Now,
We know that,
The fraction with the bigger denominator is smaller.
Hence, from the above,
We can conclude that
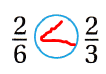
Question 5.
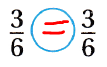
\(\frac{3}{6}\) ![]() \(\frac{3}{6}\)
\(\frac{3}{6}\)
Answer:
The given fractions are:
\(\frac{3}{6}\) and \(\frac{3}{6}\)
Now,
We know that,
The fraction with the bigger denominator is smaller.
Hence, from the above,
We can conclude that
Problem Solving
Math Talk
Mathematical Processes
Explain why \(\frac{1}{2}\) is greater than \(\frac{1}{4}\)?
Answer:
The given fractions are:
\(\frac{1}{2}\) and \(\frac{1}{4}\)
Now,
We know that,
The fraction with the bigger denominator is smaller.
Hence, from the above,
We can conclude that
\(\frac{1}{2}\) is greater than \(\frac{1}{4}\)
Question 6.
H.O.T. Write Math Zach has a piece of pie that is \(\frac{1}{4}\) of a pie. Max has a piece of pie that is of a pie. Max’s piece is smaller than Zach’s piece. Explain how this could happen. Draw a picture to show your answer.
Answer:
It is given that
Zach has a piece of pie that is \(\frac{1}{4}\) of a pie. Max has a piece of pie that is of a pie. Max’s piece is smaller than Zach’s piece.
Now,
We know that,
The fraction with the bigger denominator is smaller.
Hence, from the above,
We can conclude that
The representation of a piece of the pie of Max and Zach is:
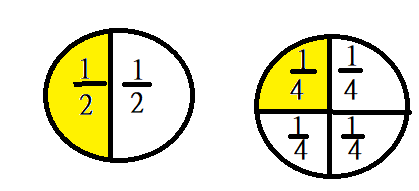
Unlock the Problem
Question 7.
Quinton and Hunter are biking on trails in Katy Trail State Park. They hiked \(\frac{5}{6}\) mile in the morning and \(\frac{5}{8}\) mile in the afternoon. Did they bike a greater distance in the morning or in the afternoon?
a. What do you need to know? ____
Answer:
It is given that
Quinton and Hunter are biking on trails in Katy Trail State Park. They hiked \(\frac{5}{6}\) mile in the morning and \(\frac{5}{8}\) mile in the afternoon
Hence, from the above,
We can conclude that
You need to know which fraction of the mile is greater
b. The numerator is 5 in both fractions, so compare \(\frac{1}{6}\) and \(\frac{1}{8}\). Explain.
Answer:
The given fractions are:
\(\frac{5}{6}\) and \(\frac{5}{8}\)
Now,
We know that,
The fraction that has the same numerator with the bigger denominator is smaller.
Hence, from the above,
We can conclude that
\(\frac{1}{6}\) > \(\frac{1}{8}\)
c. What plan or strategy will you use?
Answer:
The strategy you will use to find is:
The fraction that has the same numerator with the bigger denominator is smaller.
d. Complete the sentences.
In the morning, the boys biked \(\frac{5}{6}\) mile.
In the afternoon, the boys hiked \(\frac{5}{8}\) mile.
The boys hiked a greater distance in the afternoon.
So,
\(\frac{5}{6}\) > \(\frac{5}{8}\)
Question 8.
Multi-Step Sense or Nonsense?
James ate \(\frac{2}{4}\) of his pancake. David ate \(\frac{2}{3}\) of his pancake. Both pancakes are the same size. Who ate more of his pancake?
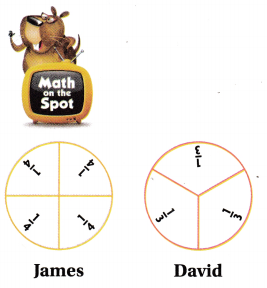
James said he knows he ate more because four is greater than three. Does his answer make sense? Shade the models. Then use math language to explain your answer.
Answer:
It is given that
James ate \(\frac{2}{4}\) of his pancake. David ate \(\frac{2}{3}\) of his pancake. Both pancakes are the same size
It is also given that
James said he knows he ate more because four is greater than three
Now,
The given fractions are:
\(\frac{2}{4}\) and \(\frac{2}{3}\)
Now,
We know that,
The fraction that has the same numerator with the bigger denominator is smaller.
So,
The representation of the models of James and David is:
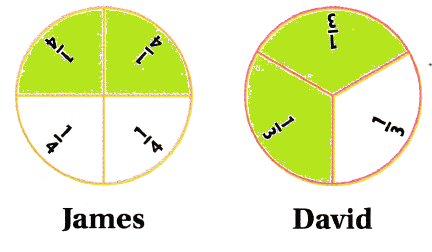
Hence, from the above,
We can conclude that
\(\frac{2}{4}\) < \(\frac{2}{3}\)
The answer of James does not make sense
Daily Assessment Task
Use models to compare. Fill in the bubble for the correct answer choice.
Question 9.
Ben, Lara, and Liz had pizza for lunch. Ben had a slice of the Mushroom pizza. Lara and Liz each ate one slice of the Olive pizza. Which fraction shows how much pizza Ben ate?
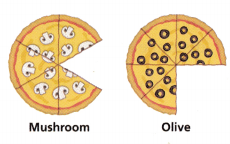
(A) \(\frac{1}{6}\)
(B) \(\frac{2}{6}\)
(C) \(\frac{1}{8}\)
(D) \(\frac{2}{8}\)
Answer:
It is given that
Ben, Lara, and Liz had pizza for lunch. Ben had a slice of the Mushroom pizza. Lara and Liz each ate one slice of the Olive pizza
Now,
The given figures are:

Now,
From the above,
We can observe that
The Mushroom pizza has 6 pieces and 1 piece is eaten by Ben
Hence, from the above,
We can conclude that
The fraction that shows the amount of pizza Ben ate is:

Question 10.
Which symbol makes this statement true?
![]()
(A) < (B) >
(C) =
(D) none
Answer:
The given fractions are:
\(\frac{2}{6}\) and \(\frac{2}{8}\)
Now,
We know that,
The fraction with the bigger denominator is smaller.
Hence, from the above,
We can conclude that
The symbol that makes the given statement true is:

Question 11.
Representations Multi-Step Three more friends joined Ben, Lara, and Liz for lunch. Mike and Tom each had one slice of the Olive pizza. Grace had a slice of the Mushroom pizza. After all of the friends had eaten lunch, which statement is true about the slices of Olive and Mushroom pizza that was left?
(A) \(\frac{2}{6}\) < \(\frac{2}{8}\)
(B) \(\frac{3}{6}\) < \(\frac{3}{8}\) (C) \(\frac{4}{6}\) > \(\frac{4}{8}\)
(D) \(\frac{5}{6}\) = \(\frac{5}{8}\)
Answer:
It is given that
Three more friends joined Ben, Lara, and Liz for lunch. Mike and Tom each had one slice of the Olive pizza. Grace had a slice of the Mushroom pizza and all of the friends had eaten lunch
Now,
The given figures are:

Now,
From the given information,
The fraction of the olive pizza is: \(\frac{4}{8}\)
The fraction of the mushroom pizza is: \(\frac{4}{6}\)
Now,
We know that,
The fraction with the bigger denominator is smaller.
Hence, from the above,
We can conclude that
The statement that is true about the slices of olive and mushroom pizza that was left is:

Texas Test Prep
Question 12.
Before taking a hike, Kate and Dylan each ate part of the same-size granola bars. Kate ate \(\frac{1}{3}\) of her bar. Dylan ate \(\frac{1}{2}\) of his bar. Which of the following correctly compares the amounts of granola bars that were eaten?
(A) \(\frac{1}{3}\) > \(\frac{1}{2}\)
(B) \(\frac{1}{2}\) < \(\frac{1}{3}\) (C) \(\frac{1}{2}\) > \(\frac{1}{3}\)
(D) \(\frac{1}{3}\) = \(\frac{1}{2}\)
Answer:
It is given that
Before taking a hike, Kate and Dylan each ate part of the same-size granola bars. Kate ate \(\frac{1}{3}\) of her bar. Dylan ate \(\frac{1}{2}\) of his bar
Now,
The given fractions are:
\(\frac{1}{3}\) and \(\frac{1}{2}\)
Now,
We know that,
The fraction with the bigger denominator is smaller.
Hence, from the above,
We can conclude that
The statement that correctly compares the amounts of granola bars that were eaten is:

Texas Go Math Grade 3 Lesson 3.2 Homework and Practice Answer Key
Question 1.
Shade the models to show \(\frac{1}{8}\) and \(\frac{1}{6}\). Then compare the fractions.
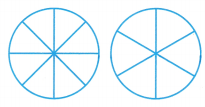
\(\frac{1}{8}\) ![]() \(\frac{1}{6}\)
\(\frac{1}{6}\)
Answer:
The given fractions are:
\(\frac{1}{8}\) and \(\frac{1}{6}\)
Now,
The representation of the given fractions in the given models is:
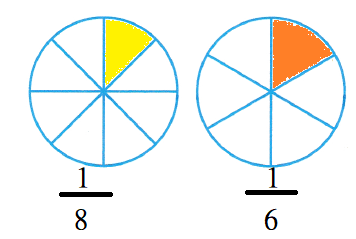
Now,
We know that,
The fraction with the bigger denominator is smaller.
Hence, from the above,
We can conclude that
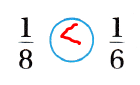
Question 2.
Shade the models to show \(\frac{3}{4}\) and \(\frac{3}{6}\). Then compare the fractions.
\(\frac{3}{4}\) ![]() \(\frac{3}{6}\)
\(\frac{3}{6}\)
Answer:
The given fractions are:
\(\frac{3}{4}\) and \(\frac{3}{6}\)
Now,
The representation of the given fractions in the given models is:
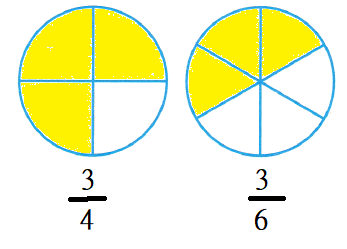
Now,
We know that,
The fraction with the bigger denominator is smaller.
Hence, from the above,
We can conclude that
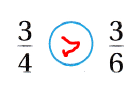
Compare. Write <, >, or =.
Question 3.
\(\frac{1}{3}\) ![]() \(\frac{1}{4}\)
\(\frac{1}{4}\)
Answer:
The given fractions are:
\(\frac{1}{3}\) and \(\frac{1}{4}\)
Now,
We know that,
The fraction with the bigger denominator is smaller.
Hence, from the above,
We can conclude that

Question 4.
\(\frac{1}{6}\) ![]() \(\frac{1}{2}\)
\(\frac{1}{2}\)
Answer:
The given fractions are:
\(\frac{1}{6}\) and \(\frac{1}{2}\)
Now,
We know that,
The fraction with the bigger denominator is smaller.
Hence, from the above,
We can conclude that

Question 5.
\(\frac{7}{8}\) ![]() \(\frac{7}{8}\)
\(\frac{7}{8}\)
Answer:
The given fractions are:
\(\frac{7}{8}\) and \(\frac{7}{8}\)
Now,
We know that,
The fraction with the bigger denominator is smaller.
Hence, from the above,
We can conclude that

Question 6.
\(\frac{2}{3}\) ![]() \(\frac{2}{6}\)
\(\frac{2}{6}\)
Answer:
The given fractions are:
\(\frac{2}{3}\) and \(\frac{2}{6}\)
Now,
We know that,
The fraction with the bigger denominator is smaller.
Hence, from the above,
We can conclude that

Problem Solving
Question 7.
Gina and Russ both order the same size sandwich. Gina eats \(\frac{2}{4}\) of her sandwich. Russ eats \(\frac{2}{6}\) of his sandwich. Who eats more of the sandwich?
Answer:
It is given that
Gina and Russ both order the same size sandwich. Gina eats \(\frac{2}{4}\) of her sandwich. Russ eats \(\frac{2}{6}\) of his sandwich
Now,
The given fractions are:
\(\frac{2}{4}\) and \(\frac{2}{6}\)
Now,
We know that,
The fraction with the bigger denominator is smaller.
So,
\(\frac{2}{4}\) > \(\frac{2}{6}\)
Hence, from the above,
We can conclude that
Gina eats more of the sandwich
Question 8.
Karina makes crafts to sell at the fair. She makes \(\frac{1}{2}\) of the crafts on Saturday and \(\frac{1}{4}\) of the crafts on Sunday. On which day did she make fewer crafts?
Answer:
It is given that
Karina makes crafts to sell at the fair. She makes \(\frac{1}{2}\) of the crafts on Saturday and \(\frac{1}{4}\) of the crafts on Sunday
Now,
The given fractions are:
\(\frac{1}{2}\) and \(\frac{1}{4}\)
Now,
We know that,
The fraction with the bigger denominator is smaller.
So,
\(\frac{1}{2}\) > \(\frac{1}{4}\)
Hence, from the above,
We can conclude that
Karina made fewer crafts on Sunday
Texas Test Prep
Lesson Check
Fill in the bubble completely to show your answer.
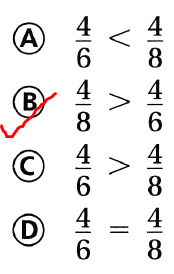
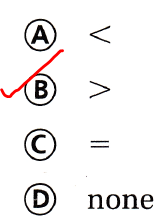
Question 9.
Which symbol makes this statement true?
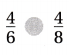
(A) < (B) >
(C) =
(D) none
Answer:
The given fractions are:
\(\frac{4}{6}\) and \(\frac{4}{8}\)
Now,
We know that,
The fraction with the bigger denominator is smaller.
Hence, from the above,
We can conclude that
The symbol that makes the given statement true is:
Question 10.
Which symbol makes the statement true?
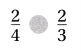
(A) < (B) >
(C) =
(D) none
Answer:
The given fractions are:
\(\frac{2}{4}\) and \(\frac{2}{3}\)
Now,
We know that,
The fraction with the bigger denominator is smaller.
Hence, from the above,
We can conclude that
The symbol that makes the given statement true is:
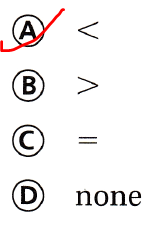
Question 11.
Hal finished \(\frac{2}{8}\) of his math problems. Aaron finished \(\frac{2}{4}\) of his math problems. Which statement is correct?
(A) \(\frac{2}{8}\) < \(\frac{2}{4}\)
(B) \(\frac{2}{8}\) = \(\frac{2}{4}\)
(C) \(\frac{2}{4}\) < \(\frac{2}{8}\) (D) \(\frac{2}{8}\) > \(\frac{2}{4}\)
Answer:
It is given that
Hal finished \(\frac{2}{8}\) of his math problems. Aaron finished \(\frac{2}{4}\) of his math problems
Now,
The given fractions are:
\(\frac{2}{8}\) and \(\frac{2}{4}\)
Now,
We know that,
The fraction with the bigger denominator is smaller.
Hence, from the above,
We can conclude that
The correct statement is:

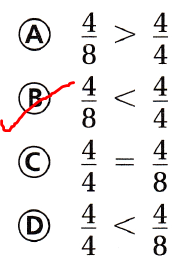
Question 12.
Sharon ate \(\frac{4}{4}\) of one orange and \(\frac{4}{8}\) of a second orange. Which statement is correct?
(A) \(\frac{4}{8}\) > \(\frac{4}{4}\)
(B) \(\frac{4}{8}\) < \(\frac{4}{4}\)
(C) \(\frac{4}{4}\) = \(\frac{4}{8}\)
(D) \(\frac{4}{4}\) < \(\frac{4}{8}\)
Answer:
It is given that
Sharon ate \(\frac{4}{4}\) of one orange and \(\frac{4}{8}\) of a second orange.
Now,
The given fractions are:
\(\frac{4}{4}\) and \(\frac{4}{8}\)
Now,
We know that,
The fraction with the bigger denominator is smaller.
Hence, from the above,
We can conclude that
The correct statement is:
Question 13.
Multi-Step Jordan ate 3 slices of cheese pizza. Then Len ate two slices of veggie pizza and 1 slice of cheese pizza. Which statement is true about the amount of leftover pizza?
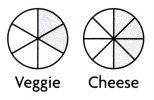
(A) \(\frac{4}{6}\) < \(\frac{4}{8}\)
(B) \(\frac{4}{8}\) > \(\frac{4}{6}\)
(C) \(\frac{4}{6}\) > \(\frac{4}{8}\)
(D) \(\frac{4}{6}\) = \(\frac{4}{8}\)
Answer:
It is given that
Jordan ate 3 slices of cheese pizza. Then Len ate two slices of veggie pizza and 1 slice of cheese pizza
Now,
The given figures are:

Now,
From the above,
We can observe that
The total number of slices of veggie pizza is: 6 slices
The total number of slices of cheese pizza is: 6 slices
Now,
From the given information,
The total number of slices of pizzas eaten by Jordan is: \(\frac{4}{6}\)
The total number of slices of pizza eaten by Len is: \(\frac{4}{8}\)
Now,
We know that,
The fraction with the bigger denominator is smaller.
Hence, from the above,
We can conclude that