Practice the questions of McGraw Hill Math Grade 8 Answer Key PDF Lesson 14.4 Slope to secure good marks & knowledge in the exams.
McGraw-Hill Math Grade 8 Answer Key Lesson 14.4 Slope
Exercises
FIND THE SLOPE
Question 1.
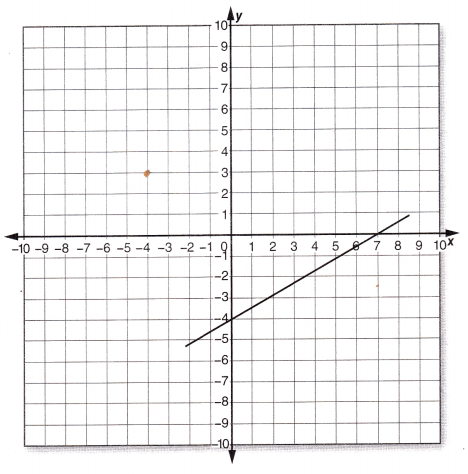
Answer:
\(\frac{5.6}{10}\),
Explanation:
Using two of the points on the line, we can find the slope of the line by
finding the rise and the run. The vertical change between two points is
called the rise and the horizontal change is called the run. The slope equals the rise divided by the run:
Slope =rise ÷ run = (y2 – y1) ÷ (x2 – x1),
We have given points as (-2, -5.1) and (8, 0.5),
So slope = (0.5 – (-5.1))/ (8 -(-2)) = 5.6/10.
Question 2.
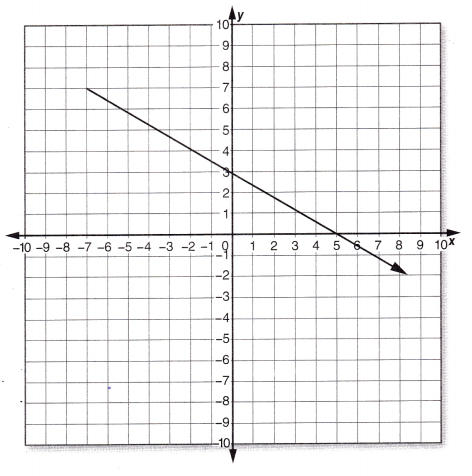
Answer:
–\(\frac{8.1}{14}\),
Explanation:
Using two of the points on the line, we can find the slope of the line by
finding the rise and the run.
The vertical change between two points is called the rise and the horizontal change is called the run. The slope equals the rise divided by the run:
Slope =rise ÷ run = (y2 – y1) ÷ (x2 – x1),
We have given points as (-7, 7) and (7, -1.1),
So slope = (-1.1 – 7)/ (7 -(-7)) = -8.1/14.
Question 3.
y = 6x – 2
Answer:
Slope is 6,
Explanation:
A slope of a line is the change in y coordinate with respect to
the change in x coordinate. The equation of the line is written in the
slope-intercept form, which is: y = mx + b,
where m represents the slope and b represents the y-intercept.
Therefore the given line y = 6x – 2 has slope 6.
Question 4.
y – x = 4
Answer:
Slope is 1,
Explanation:
A slope of a line is the change in y coordinate with respect to
the change in x coordinate.
The equation of the line is written in the slope-intercept form,
which is: y = mx + b, where m represents the slope and b represents
the y-intercept. Therefore the given line y – x = 4, y = x + 4 has slope 1.
Question 5.
-3 = \(\frac{2}{3}\)x – y
Answer:
Slope is \(\frac{2}{3}\),
Explanation:
A slope of a line is the change in y coordinate with respect to
the change in x coordinate.
The equation of the line is written in the slope-intercept form,
which is: y = mx + b, where m represents the slope and
b represents the y-intercept.
Therefore the given line -3 = \(\frac{2}{3}\)x – y
y = \(\frac{2}{3}\)x + 3 has slope \(\frac{2}{3}\).
Question 6.
x + y = -5
Answer:
Slope is -1,
Explanation:
A slope of a line is the change in y coordinate with respect to
the change in x coordinate.
The equation of the line is written in the slope-intercept form,
which is: y = mx + b, where m represents the slope and b represents
the y-intercept.
Therefore the given line x + y = -5, y = -x – 5 = (-1)x – 5 has slope -1.