McGraw Hill Math Grade 8 Lesson 14.2 Answer Key Function Tables

by

Practice the questions of McGraw Hill Math Grade 8 Answer Key PDF Lesson 14.2 Function Tables to secure good marks & knowledge in the exams.

McGraw-Hill Math Grade 8 Answer Key Lesson 14.2 Function Tables

Exercises

CALCULATE

Fill in the corresponding values of y for the given x value in the function table.

Question 1.
y = x + 1
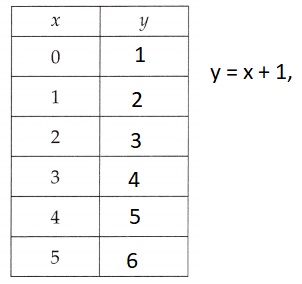
McGraw Hill Math Grade 8 Lesson 14.2 Answer Key Function Tables 1
Answer:
McGraw Hill Math Grade 8 Lesson 14.2 Answer Key Function Tables-1

Explanation:
Filled in the corresponding values of y for the given equation y = x + 1,
x value in the function table as  if x = 0 then y = 0 + 1 = 1,
if x = 1 then y = 1+1 = 2, if x = 2 then y = 2+ 1 = 3,
if x = 3 then y = 3 + 1 = 4, if x = 4 then y = 4 + 1 = 5 and
if x = 5 then y = 5 + 1 = 6 above.

Question 2.
y = 2x + 2
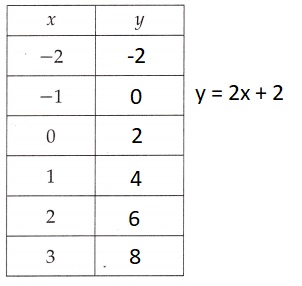
McGraw Hill Math Grade 8 Lesson 14.2 Answer Key Function Tables 2
Answer:
McGraw Hill Math Grade 8 Lesson 14.2 Answer Key Function Tables-2

Explanation:
Filled in the corresponding values of y for the given equation y = 2x + 2,
x value in the function table as if x = -2 then y = 2 X -2 + 2 = -4 + 2 = -2,
if x = -1 then y = 2 X -1 + 2 = -2 + 2 = 0,
if x = 0 then y = 2 X 0 + 2 = 0 + 2 = 2,
if x = 1 then y = 2 X 1 + 2 = 2 + 2 = 4,
if x =  2 then y = 2 X 2 + 2 = 4 + 2 = 6 and
if x = 3 then y = 2 X 3 + 2 = 6 + 2 = 8.

Question 3.
y = x – 4
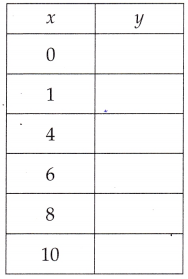
McGraw Hill Math Grade 8 Lesson 14.2 Answer Key Function Tables 3
Answer:
McGraw Hill Math Grade 8 Lesson 14.2 Answer Key Function Tables-3

Explanation:
Filled in the corresponding values of y for the given equation y = x – 4,
x value in the function table as if x = 0 then y = 0 – 4 = -4,
if x = 1 then y = 1 – 4 = -3, if x = 4 then y = 4 – 4 = 0,
if x = 6 then y = 6 – 4 = 2, if x =  8 then y = 8 – 4 = 4 and
if x = 10 then y = 10 – 4 = 6.

Question 4.
y = 2x – 3
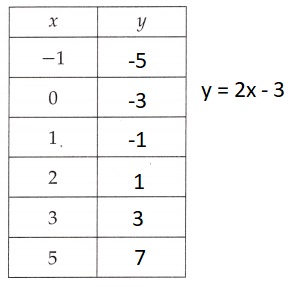
McGraw Hill Math Grade 8 Lesson 14.2 Answer Key Function Tables 4
Answer:
McGraw Hill Math Grade 8 Lesson 14.2 Answer Key Function Tables-4

Explanation:
Filled in the corresponding values of y for the given equation y = 2x – 3,
x value in the function table as
if x = -1 then y = 2 X -1 – 3 = -2 – 3 = -5,
if x = 0 then y = 2 X 0 – 3 = 0 – 3 = -3,
if x = 1 then y = 2 X 1 – 3 = 2 – 3 = -1,
if x = 2 then y = 2 X 2 – 3 = 4 – 3 = 1,
if x = 3 then y = 2 X 3 – 3 = 6 – 3 = 3 and
if x = 5 then y = 2 X 5 – 3 = 10 – 3 = 7.

Question 5.
y = 2x + 1
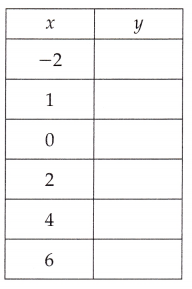
McGraw Hill Math Grade 8 Lesson 14.2 Answer Key Function Tables 5
Answer:
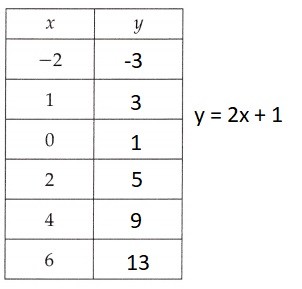
McGraw Hill Math Grade 8 Lesson 14.2 Answer Key Function Tables-5

Explanation:
Filled in the corresponding values of y for the given equation y = 2x + 1,
x value in the function table as
if x = -2 then y = 2 X -2 + 1 = -4 + 1 = -3,
if x = 1 then y = 2 X 1 + 1 = 2 + 1 = 3,
if x = 0 then y = 2 X 0 + 1 = 0 + 1 = 1,
if x = 2 then y = 2 X 2 + 1 = 4 + 1 = 5,
if x = 4 then y = 2 X 4 + 1 = 8 + 1 = 9 and
if x = 6 then y = 2 X 6 + 1 = 12 + 1 = 13.

Question 6.
y = \(\frac{1}{2}\)x + 1
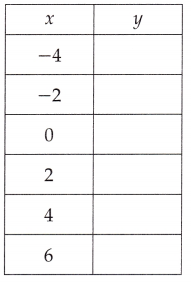
McGraw Hill Math Grade 8 Lesson 14.2 Answer Key Function Tables 6
Answer:
McGraw Hill Math Grade 8 Lesson 14.2 Answer Key Function Tables-6

Explanation:
Filled in the corresponding values of y for the given equation
y = \(\frac{1}{2}\)x + 1, x value in the function table as
if x = -4 then y = \(\frac{1}{2}\) X -4 + 1= -2 + 1 = -1,
if x = -2 then y = \(\frac{1}{2}\) X -2 + 1 = 2 + 1 = 0,
if x = 0 then y = \(\frac{1}{2}\) X 0 + 1 = 0 + 1 = 1,
if x = 2 then y = \(\frac{1}{2}\) X 2 + 1 = 1 + 1 = 2,
if x = 4 then y = \(\frac{1}{2}\) X 4 + 1 = 2 + 1 = 3 and
if x = 6 then y = \(\frac{1}{2}\) X 6 + 1 = 3 + 1 = 4.

Identify the function by looking at the ordered pairs (x, y) in the function table.

Question 7.
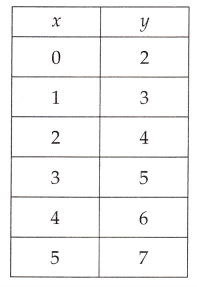
McGraw Hill Math Grade 8 Lesson 14.2 Answer Key Function Tables 7
Answer:
f(y) = x + 2,

Explanation:
If we see the values of y it is 2 more than x in each case,
therefore function of the ordered pairs is f(y) = x + 2.

Question 8.
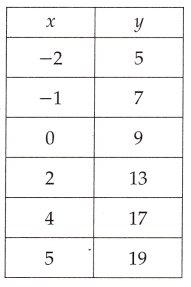
McGraw Hill Math Grade 8 Lesson 14.2 Answer Key Function Tables 8
Answer:
f(y) = 2x + 9,

Explanation:
If we see the values of y it is 2x and 9 more in each case,
therefore function of the ordered pairs is f(y) = 2x + 9.

Question 9.
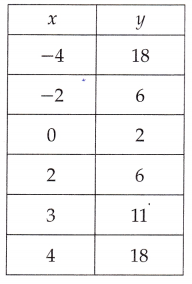
McGraw Hill Math Grade 8 Lesson 14.2 Answer Key Function Tables 9
Answer:
f(y) = x2 + 2,

Explanation:
If we see the values of y it is square of x and 2 more in each case,
therefore function of the ordered pairs is f(y) = x + 2.

Question 10.
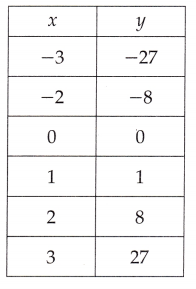
McGraw Hill Math Grade 8 Lesson 14.2 Answer Key Function Tables 10
Answer:
f(y) = x3,

Explanation:
If we see the values of y it is cube of x,
therefore function of the ordered pairs is f(y) = x3.

Complete the function table and then graph the function.

Question 11.
y = 3x – 3
McGraw Hill Math Grade 8 Lesson 14.2 Answer Key Function Tables 11
Answer:
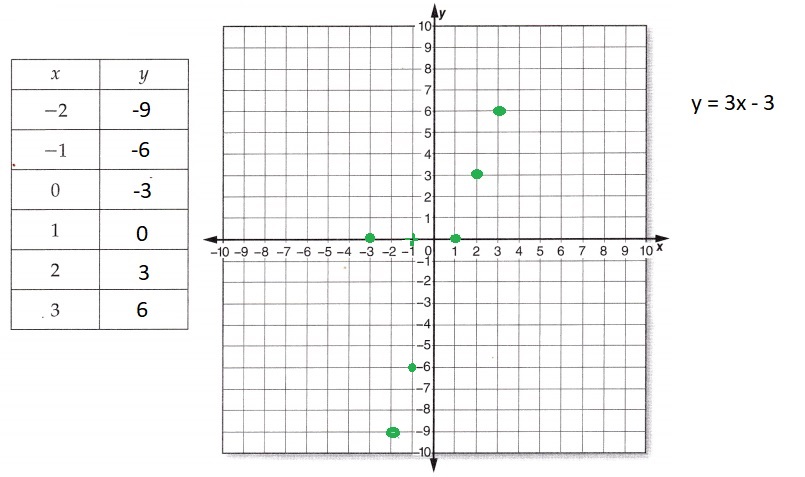
McGraw Hill Math Grade 8 Lesson 14.2 Answer Key Function Tables-7

Explanation:
Completed the function y = 3x – 3 in the table for values of
y for x value in the function table as
if x = -2 then y = 3 X -2 – 3 = -6 – 3 = -9,
if x = -1 then y = 3 X -1 – 3 = -3 – 3 = -6,
if x = 0 then y = 3 X 0 – 3 = 0 – 3 = -3,
if x = 1 then y = 3 X 1 – 3 = 3 – 3 = 0,
if x = 2 then y = 3 X 2 – 3 = 6 – 3 = 3 and
if x = 3 then y = 3 X 3 – 3 = 6.

Question 12.
y = x2
McGraw Hill Math Grade 8 Lesson 14.2 Answer Key Function Tables 12
Answer:
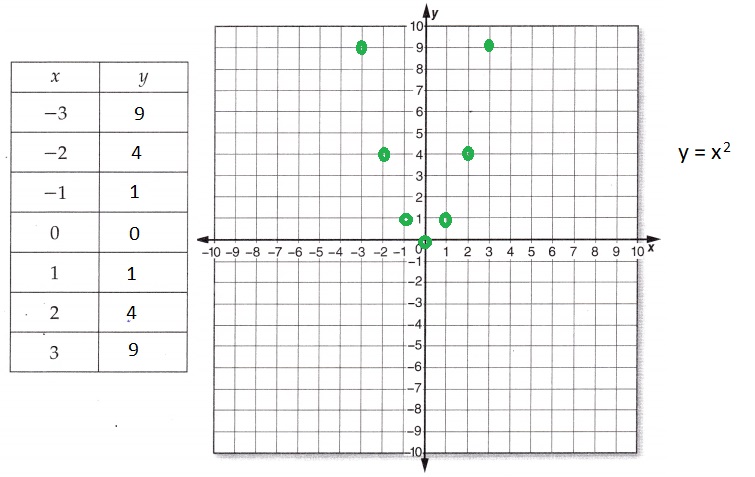
McGraw Hill Math Grade 8 Lesson 14.2 Answer Key Function Tables-8

Explanation:
Completed the function y = x2 in the table for values of
y for x value in the function table as
if x = -3 then y = (-3)2 = – 3 X – 3 = 9,
if x = -2 then y = (-2)2 =  -2 X -2 = 4,
if x = -1 then y = (-1)2 = -1 X -1 = 1,
if x = 0 then y = (0)2 = 0 X 0 = 0,
if x = 1 then y = (1)2 = 1 X 1 = 1,
if x = 2 then y = (2)2 = 2 X 2 = 4 and
if x = 3 then y = (3)2 = 3 X 3 = 6.

Leave a Comment