McGraw Hill Math Grade 6 Pretest Answer Key

Practice questions available in McGraw Hill Math Grade 6 Answer Key PDF Pretest will engage students and is a great way of informal assessment.

McGraw-Hill Math Grade 6 Pretest Answer Key

Complete the following test items.

Question 1.
The Mayor of Tampa told Angela that there are three hundred thousand, six hundred, thirty five people living in their city. When she writes this number in standard form, Angela will write ______________
Answer:
Standard form: 300,635.

Explanation:
Number of people living in their city = three hundred thousand, six hundred, thirty five
Standard form: 300,000 + 600 + 35
= 300,600 + 35
= 300,635.

Question 2.
Yousef is collecting signatures to build a park in his town. He needs 8,000 signatures to submit his petition. So far he has collected 2,875. Rounding to the nearest thousand, how many signatures can we estimate Yousef still needs to collect? ______________________
Answer:
Number of signatures he needs to collect = 5,125.

Explanation:
Number of signatures to submit his petition he needs = 8,000.
Number of signatures he has collected = 2,875.
Number of signatures he needs to collect = Number of signatures to submit his petition he needs – Number of signatures he has collected
= 8,000 – 2,875
= 5,125.
Rounding to the nearest thousand:
5,125 – 5,000.

Calculate.
Question 3.

Answer:

Explanation:
48 multiplied by 19, we get the product 912.

Question 4.

Answer:

Explanation:
55 multiplied by 15, we get the product 825.

Question 5.
|-\(\frac{5}{6}\)|
Answer:
|-\(\frac{5}{6}\)| = \(\frac{5}{6}\)

Explanation:
Absolute value of |-\(\frac{5}{6}\)| = \(\frac{5}{6}\)

Question 6.
|0.02|
Answer:
|0.02| = 0.02

Explanation:
Absolute value of |0.02| = 0.02

Question 7.
Miguel bought 11 cheese pizzas for his math dub at school, but the club members only ate half of each pizza. How would Miguel express the amount of remaining pizza as an improper fraction? How would Miguel express the amount of remaining pizza as a mixed number?
Answer:
Amount of remaining pizza as an improper fraction = \(\frac{11}{2}\)
Amount of remaining pizza as an mixed fraction = 5\(\frac{1}{2}\)

Explanation:
Number of cheese pizzas for his math dub at school Miguel bought = 11.
Number of cheese pizzas the club members only ate = half of each pizza.
Amount of remaining pizza = Number of cheese pizzas for his math dub at school Miguel bought ÷ 2
= 11 ÷ 2
= 5.5 or \(\frac{11}{2}\) or 5\(\frac{1}{2}\)

Calculate.
Question 8.

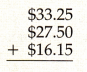
Answer:

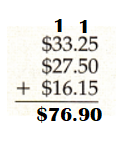
Explanation:
Sum of $33.25 + $27.50 + $16.15
= $60.75 + $16.15
= $76.90.

Question 9.

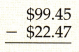
Answer:

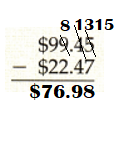
Explanation:
Difference between $99.45 and $22.47

Question 10.
What is the least common multiple of 6 and 9?
Answer:
Least common multiple of 6 and 9 = 18.

Explanation:
Least common multiple of 6 and 9:
Multiples of 6: 6,12,18,24,30,36,42,48,54,60.
Multiples of 9: 9,18,27,36,45,54,63,72,81,90.

Question 11.
What is the greatest common factor of 6 and 18?
Answer:
Greatest common factor of 6 and 18 = 2.

Explanation:
Greatest common factor of 6 and 18:
Factor of 6:
1,2,3,6.
Factor of 8:
1,2,4,8.

Question 12.
George has been measuring the amount of rainfall for the last three months. He measured 3.562 inches in April, 2.765 inches in May, and 3.015 inches in June. Rounding to the nearest tenth of an inch, what was the total amount of rainfall during these three months? ______________
Answer:
Amount of rainfall for the last three months he measured = 9.342.

Explanation:
Number of inches of rainfall he measured in April = 3.562.
Number of inches of rainfall he measured in May = 2.765.
Number of inches of rainfall he measured in June = 3.015
Amount of rainfall for the last three months he measured = Number of inches of rainfall he measured in April + Number of inches of rainfall he measured in May + Number of inches of rainfall he measured in June
= 3.562 + 2.765 + 3.015
= 6.327 + 3.015
= 9.342.
Rounding to the nearest tenth of an inch:
9.342 – 10.

Calculate.
Question 13.

Answer:

Explanation:
Dividing 1951 by 78, we get the quotient 25.01.

Question 14.

Answer:

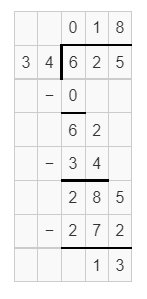
Explanation:
Dividing 625 by 34, we get the quotient 18.38.

Question 15.

Answer:

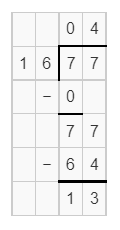
Explanation:
Dividing 77 by 16, we get the quotient 4.812.

Question 16.

Answer:

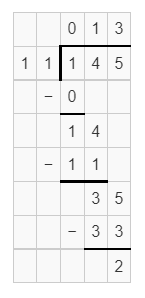
Explanation:
Dividing 145 by 11, we get the quotient 13.18.

Question 17.
Kaleigh is mixing paint for art class. The directions call for her to mix 17.25 milliliters of blue paint and 13.45 milliliters of yellow paint to achieve the right shade of green for her assignment. How much blue paint and how much yellow paint will she need in order to mix the right amount of paint for herself and two other classmates? _________
About how much green paint will she be making, altogether, for the three of them ? ______________
Answer:
Number of milliliters of blue paint and yellow paint she will need in order to mix the right amount of paint for herself and two other classmates = 92.10.

Explanation:
Number of milliliters of blue paint the directions call for her to mix = 17.25
Number of milliliters of yellow paint the directions call for her to mix = 13.45
Number of milliliters of blue paint and yellow paint she will need in order to mix the right amount of paint for herself = Number of milliliters of blue paint the directions call for her to mix + Number of milliliters of yellow paint the directions call for her to mix
= 17.25 + 13.45
= 30.70.
Number of milliliters of blue paint and yellow paint she will need in order to mix the right amount of paint for herself and two other classmates = Number of milliliters of blue paint and yellow paint she will need in order to mix the right amount of paint for herself  + 2(Number of milliliters of blue paint and yellow paint she will need in order to mix the right amount of paint for herself)
= 30.70 + 2(30.70)
= 30.70 + 61.40
= 92.10.

Question 18.
What is 60% of 120? _____
Answer:
60% of 120 = 72.

Explanation:
60% of 120 = \(\frac{60}{100}\) × 120
= \(\frac{6}{10}\) × 120
= \(\frac{6}{1}\) × 12
= 72.

Question 19.
What is 40% of \(\frac{3}{4}\)? Express the number in both decimal and fraction form.
Answer:
40% of \(\frac{3}{4}\)
Decimal form = 0.3
Fraction form = \(\frac{3}{10}\)

Explanation:
40% of \(\frac{3}{4}\)
= 40% × \(\frac{3}{4}\)
= \(\frac{40}{100}\) × \(\frac{3}{4}\)
= \(\frac{10}{100}\) × \(\frac{3}{1}\)
= \(\frac{1}{10}\) × \(\frac{3}{1}\)
= \(\frac{3}{10}\) or 0.3.

Question 20.
Terrence has a length of rope that is 14\(\frac{3}{4}\) meters long. Forty percent of the rope’s length is covered by a plastic film that makes it waterproof. What length of the rope is not waterproof?
Express your answer as a mixed fraction. ________________________
Answer:
Number of meters of the rope is not waterproof as a mixed fraction = 5\(\frac{9}{10}\)

Explanation:
Number of meters of rope Terrence has = 14\(\frac{3}{4}\)
Forty percent of the rope’s length is covered by a plastic film that makes it waterproof.
=> Number of meters of the rope is not waterproof = 40% × Number of meters of rope Terrence has
= 40% × 14\(\frac{3}{4}\)
= 40% × {[(14 × 4) + 3] ÷ 4}
= 40% × [(56 + 3) ÷ 4]
= 40% × (59 ÷ 4)
= \(\frac{40}{100}\) × \(\frac{59}{4}\)
= \(\frac{4}{10}\) × \(\frac{59}{4}\)
= \(\frac{1}{10}\) × \(\frac{59}{1}\)
= \(\frac{59}{10}\)  or 5.9 or 5\(\frac{9}{10}\)

Question 21.
1f x + 4 ≥ 12, could the value of x be 10? ___________ Could x be 8? ______
Answer:
Yes, x + 4 ≥ 12 is a true statement of x = 8 and 10.

Explanation:
x + 4 ≥ 12,
Let x = 10
=> x + 4 ≥ 12
=> 10 + 4 ≥ 12
=> 14 ≥ 12
Let x = 8.
=> x + 4 ≥ 12
=> 8 + 4 ≥ 12
=> 12 ≥ 12

Question 22.
Maynard bought a scale that records weight digitally. His math book weighs 2 kilograms, his science workbook weighs \(\frac{3}{4}\) of a kilogram, his social studies book weighs 1\(\frac{1}{3}\) kilograms, and his language arts book weighs 3\(\frac{1}{2}\) kilograms. What is the total weight of the four hooks, in kilograms? ___________
If a student is only allowed to carry 12.25 kilograms of books, will Maynard’s four books exceed the limit? ___________
Answer:
Number of kilograms the total weight of the four books = \(\frac{91}{12}\) or 7.58.
No, Maynard’s four books exceed the limit will not exceed if a student is only allowed to carry 12.25 kilograms of books.

Explanation:
Number of kilograms his math book weighs = 2.
Number of kilograms his science book weighs = \(\frac{3}{4}\)
Number of kilograms his social book weighs = 1\(\frac{1}{3}\)
Number of kilograms his art book weighs = 3\(\frac{1}{2}\)
Number of kilograms the total weight of the four books = Number of kilograms his math book weighs + Number of kilograms his science book weighs + Number of kilograms his social book weighs + Number of kilograms his art book weighs
= 2 + \(\frac{3}{4}\) + 1\(\frac{1}{3}\) + 3\(\frac{1}{2}\)
= 2 + \(\frac{3}{4}\) + {[(1 × 3) + 1] ÷ 3} + {[(3 × 2) + 1] ÷ 2}
= 2 + \(\frac{3}{4}\) + [(3 + 1) ÷ 3] + [(6 + 1) ÷ 2]
= 2 + \(\frac{3}{4}\) + \(\frac{4}{3}\) + \(\frac{7}{2}\)
= 2 +
= 2 + \(\frac{67}{12}\)

 

 

Question 23.

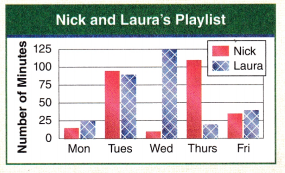
The chart shows how much time Nick and Laura spent last week listening to their favorite music. On which day did Laura listen to 90 minutes of music?
___________________
On which day did Nick listen to music 85 minutes longer than Laura?
__________________
Answer:
On Tuesday Laura listen to 90 minutes of music.
Thursday Nick listen to music 85 minutes longer than Laura.

Explanation:
Nick timings:
Number of minutes Nick spent last week listening to their favorite music on Monday = 15.
Number of minutes Nick spent last week listening to their favorite music on Tuesday = 90.
Number of minutes Nick spent last week listening to their favorite music on Wednesday = 10.
Number of minutes Nick spent last week listening to their favorite music on Thursday = 105.
Number of minutes Nick spent last week listening to their favorite music on Friday = 40.
Laura Timings:
Number of minutes Laura spent last week listening to their favorite music on Monday = 25.
Number of minutes Laura spent last week listening to their favorite music on Tuesday = 90.
Number of minutes Laura spent last week listening to their favorite music on Wednesday = 125.
Number of minutes Laura spent last week listening to their favorite music on Thursday = 20.
Number of minutes Laura spent last week listening to their favorite music on Friday = 30.
Difference:
Number of minutes Nick spent last week listening to their favorite music on Thursday – Number of minutes Laura spent last week listening to their favorite music on Thursday
= 105 – 20
= 85.

Question 24.

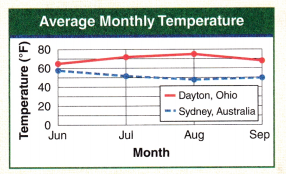
Which city is colder in June?
During which month is the difference in temperature the greatest?
Answer:
August month is the difference in temperature the greatest.

Explanation:
Dayton, Ohio temperature:
Temperature of Dayton, Ohio in June = 65°F
Temperature of Dayton, Ohio in July = 70°F
Temperature of Dayton, Ohio in August = 75°F
Temperature of Dayton, Ohio in September = 70°F
Sydney, Australia temperature:
Temperature of Sydney, Australia in June = 60°F
Temperature of Sydney, Australia in July = 50°F
Temperature of Sydney, Australia in August = 45°F
Temperature of Sydney, Australia in September = 50°F
Difference:
Temperature of Dayton, Ohio in June – Temperature of Sydney, Australia in June
= 65°F – 60°F
= 5°F
Temperature of Dayton, Ohio in July – Temperature of Sydney, Australia in July
= 70°F – 50°F
= 20°F
Temperature of Dayton, Ohio in August  – Temperature of Sydney, Australia in august
= 75°F – 45°F
= 30°F
Temperature of Dayton, Ohio in September  – Temperature of Sydney, Australia in September
= 70°F – 50°F
= 20°F

Question 25.
Travis is looking at a solid figure that has a circular base, with curved sides that meet at a single point. What shape is he looking at?
Answer:
Sphere shape is he looking at.

Explanation:
Travis is looking at a solid figure that has a circular base, with curved sides that meet at a single point.
=> A sphere is a solid figure which all the points on the round surface area with curved sides that meet at a single point

Question 26.
Fiona puts three small oranges, two apples, five pears, and ten carrots into a basket. What is the probability that if she reaches into the basket that she will pick a fruit? ______________
Answer:
Probability that she reaches into the basket that she will pick a fruit = \(\frac{10}{20}\)

Explanation:
Number of oranges Fiona puts into a basket = 3.
Number of apples Fiona puts into a basket = 2.
Number of pears Fiona puts into a basket = 5.
Number of carrots Fiona puts into a basket = 10.
Total number of fruits Fiona puts into a basket = Number of oranges Fiona puts into a basket + Number of apples Fiona puts into a basket + Number of pears Fiona puts into a basket + Number of carrots Fiona puts into a basket
= 3 + 2 + 5 + 10
= 5 + 5 + 10
= 10 + 10
= 20.
Total number of fruits = Number of orange Fiona puts into a basket  + Number of apples Fiona puts into a basket + Number of pear Fiona puts into a basket
= 3 + 2 + 5
= 5 + 5
= 10.
Probability that she reaches into the basket that she will pick a fruit = Total number of fruits ÷Total number of fruits Fiona puts into a basket
= 10 ÷ 20
= \(\frac{10}{20}\)
Probability that she reaches into the basket that she will pick a orange fruit = Number of oranges Fiona puts into a basket  ÷ Total number of fruits Fiona puts into a basket ÷
= 3 ÷ 20
= \(\frac{3}{20}\)
Probability that she reaches into the basket that she will pick a apple fruit =  Number of apple Fiona puts into a basket  ÷ Total number of fruits Fiona puts into a basket
= 2 ÷ 20
= \(\frac{2}{20}\)
Probability that she reaches into the basket that she will pick a pear fruit = Number of pear Fiona puts into a basket  ÷  Total number of fruits Fiona puts into a basket
= 5 ÷ 20
= \(\frac{5}{20}\)
Probability that she reaches into the basket that she will pick a carrot = Number of carrot Fiona puts into a basket  ÷ Total number of fruits Fiona puts into a basket
= 10 ÷ 20
= \(\frac{10}{20}\)

Question 27.
Which of the following triangles is
obse? ______
right ? _____

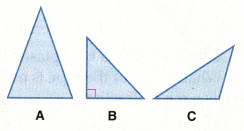
acute? ___________
Answer:
Obtuse triangle: C
Right triangle: B
Acute triangle: A

Explanation:
An obtuse triangle (or obtuse-angled triangle) is a triangle with one obtuse angle (greater than 90°) and two acute angles.
obtuse: C
A right-angled triangle is a type of triangle that has one of its angles equal to 90 degrees.
right: B
An acute triangle (or acute-angled triangle) is a  triangle with three acute angles (less than 90°).
acute: A

Question 28.
Calculate the following expression: 5 + (7 — 4)² + 4(3 + 2) – 6(2) = _____
Answer:
5 + (7 — 4)² + 4(3 + 2) – 6(2) = 22.

Explanation:
5 + (7 — 4)² + 4(3 + 2) – 6(2)
= 5 + (3)² + 4(3 + 2) – 6(2)
= 5 + (3)² + 4(5) – 6(2)
= 5 + 9 + 4(5) – 6(2)
= 5 + 9 + 20 – 6(2)
= 5 + 9 + 20 – 12
= 14 + 20 – 12
= 34 – 12
= 22.

Question 29.
Write the following number using scientific notation: 1,678,483.0043.
Answer:
Scientific notation of 1,678,483.0043 = 1,678,483.43x 10^-2.

Explanation:
Scientific notation: 1,678,483.0043.
1,678,483.43x 10^-2.

Question 30.
Leslie collects teacups and saucers. Her collection consists of 3 teacups and 2 saucers from England, 2 teacups and 4 saucers from France, and 3 teacups from Japan. If each teacup costs $9 and each saucer costs $7, how much did Leslie spend for her collection? ______________
Answer:
Amount of money she spent on her collection = $114.

Explanation:
Number of teacups from England she collects = 3.
Number of saucers from England she collects = 2.
Number of teacups from France she collects = 2.
Number of saucers from France she collects = 4.
Number of teacups from Japan she collects = 3.
Cost of each teacup = $9.
Cost of each saucer = $7.
Amount of money she spent on her collection = [Cost of each teacup × (Number of teacups from England she collects + Number of teacups from France she collects + Number of teacups from Japan she collects)] + [Cost of each saucer × (Number of saucers from England she collects + Number of saucers from France she collects)
= [$9 × (3 + 2 + 3)] + [$7 × (2 + 4)]
= ($9 × 8) + ($7 × 6)
= $72 + $42
= $114.

Question 31.
Which of the following angles is
acute? _____

right? __________
obtuse? ______
Answer:
Obtuse triangle: C
Right triangle: D
Acute triangle: E

Explanation:
An obtuse triangle (or obtuse-angled triangle) is a triangle with one obtuse angle (greater than 90°) and two acute angles.
obtuse: C
A right-angled triangle is a type of triangle that has one of its angles equal to 90 degrees.
right: D
An acute triangle (or acute-angled triangle) is a  triangle with three acute angles (less than 90°).
acute: E

Question 32.
32 ÷ .25 = ____
Answer:

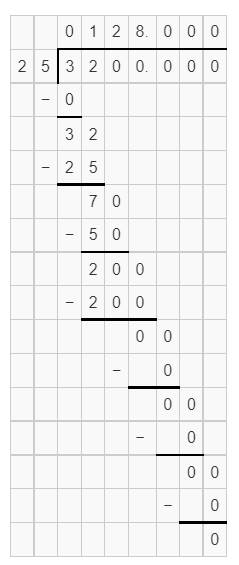
Explanation:
Dividing 32 by .25, we get the quotient 128.

Question 33.
.2505 ÷ .05 = ____
Answer:

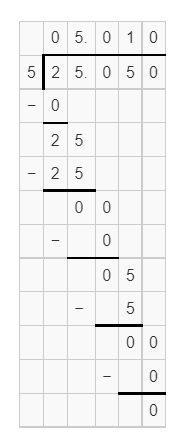
Explanation:
Dividing .2505 by .05, we get the quotient 5.01.

Question 34.
What is \(\frac{24}{35}\) ÷ 6?
Answer:
\(\frac{24}{35}\) ÷ 6 = \(\frac{4}{35}\)

Explanation:
\(\frac{24}{35}\) ÷ 6
= \(\frac{24}{35}\) × \(\frac{1}{6}\)
= \(\frac{4}{35}\) × \(\frac{1}{1}\)
= \(\frac{4}{35}\)

Question 35.
What is 16 ÷ \(\frac{8}{17}\)?
Answer:
16 ÷ \(\frac{8}{17}\) = 34.

Explanation:
16 ÷ \(\frac{8}{17}\)
= 16 × \(\frac{17}{8}\)
= 4 × \(\frac{17}{2}\)
= 2 × \(\frac{17}{1}\)
= 34.

Question 36.
What is \(\frac{32}{57}\) ÷ \(\frac{16}{19}\)?
Answer:
\(\frac{32}{57}\) ÷ \(\frac{16}{19}\) = \(\frac{2}{3}\)

Explanation:
\(\frac{32}{57}\) ÷ \(\frac{16}{19}\)
= \(\frac{32}{57}\) × \(\frac{19}{16}\)
= \(\frac{2}{57}\) × \(\frac{19}{1}\)
= \(\frac{2}{3}\) × \(\frac{1}{1}\)
= \(\frac{2}{3}\)

Question 37.
Harry is distributing rations for the class hike to the nature conservancy. Each student will carry \(\frac{3}{4}\) liters of water and \(\frac{1}{3}\) pound of trail mix for consumption during the trip. If there are 24 students on the trip, how much water and trail mix should Harry bring to distribute?
Answer:
Quantity of water and trail mix should Harry should bring to distribute = 26.
Quantity of water should Harry should bring to distribute = 18.
Quantity of trail mix should Harry should bring to distribute = 6.

Explanation:
Number of liters of water each student will carry = \(\frac{3}{4}\)
Number of pounds of trail mix each student will carry = \(\frac{1}{3}\)
Number of students in the trip = 24.
Quantity of water and trail mix should Harry should bring to distribute = (Number of students in the trip × Number of liters of water each student will carry) + (Number of students in the trip × Number of pounds of trail mix each student will carry)
= (24 × \(\frac{3}{4}\) ) + (24 × \(\frac{1}{3}\))
= (6 × \(\frac{3}{1}\) ) + (8 × \(\frac{1}{1}\))
= \(\frac{18}{1}\) + \(\frac{8}{1}\)
= 18 + 8
= 26.

Question 38.
Last week Jonas spent 9\(\frac{1}{6}\) hours working on his homework over a period of 4\(\frac{2}{3}\) days. Approximately how many hours a day, on average, did Jonas spend on his homework? _____________
Answer:
Number of hours a day, on average, did Jonas spend on his homework = \(\frac{385}{9}\) or 42\(\frac{7}{9}\)

Explanation:
Number of hours working on his homework last week Jonas spent = 9\(\frac{1}{6}\)
Number of days = 4\(\frac{2}{3}\)
Number of hours a day, on average, did Jonas spend on his homework = Number of hours working on his homework last week Jonas spent ÷ Number of days
= 9\(\frac{1}{6}\) ÷ 4\(\frac{2}{3}\)
= {[(9 × 6) + 1] ÷ 6} ÷ {[(4 × 3) + 2] ÷ 3}
= [(54 + 1) ÷ 6] ÷ [(12 + 2) ÷ 3
= (55 ÷ 6) ÷ (14 ÷ 3)
= \(\frac{55}{6}\) × \(\frac{14}{3}\)
= \(\frac{55}{3}\) × \(\frac{7}{3}\)
= \(\frac{385}{9}\) or 42\(\frac{7}{9}\)

Question 39.
What is the decimal form of 7\(\frac{7}{8}\)?
Answer:
Decimal form of 7\(\frac{7}{8}\) = 7.875.

Explanation:
7\(\frac{7}{8}\) = {[(7 × 8) + 7] ÷ 8}
= [(56 + 7) ÷ 8]
= (63 ÷ 8)
= 7.875.

Question 40.
What is the fraction form of 1.2?
Answer:
Fraction form of 1.2 : 2.4 ÷ 2

Explanation:
Fraction form of 1.2:
1.2 × 2 = 2.4.

Question 41.
Freda is making a batch of multi-grain bread for the school picnic. Each loaf requires 1\(\frac{1}{2}\) cups of flour and \(\frac{3}{4}\) cups of water. Create a ratio table to show the amounts Freda will need to make 2, 3, or 4 loaves of bread.
Answer:

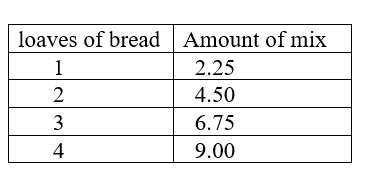
Explanation:
Number of cups of  flour each loaf requires = 1\(\frac{1}{2}\)
Number of cups of water each loaf requires = \(\frac{3}{4}\)
Amount of cups Freda will need to make a loaves of bread = Number of cups of  flour each loaf requires + Number of cups of water each loaf requires
= 1\(\frac{1}{2}\) + \(\frac{3}{4}\)
= {[(1 ×2) + 1] ÷ 2} + \(\frac{3}{4}\)
= [(2 + 1) ÷ 2] + \(\frac{3}{4}\)
= (3 ÷ 2) + \(\frac{3}{4}\)
= \(\frac{3}{2}\) + \(\frac{3}{4}\)

Amount of cups Freda will need to make a loaves of bread = \(\frac{9}{4}\)
Amount of cups Freda will need to make two loaves of bread = 2 × \(\frac{9}{4}\)
= 1 × \(\frac{9}{2}\)
= \(\frac{9}{2}\) or 4\(\frac{1}{2}\) or 4.5
Amount of cups Freda will need to make three loaves of bread = 3 × \(\frac{9}{4}\)
= \(\frac{27}{4}\) or  6.75 or 6\(\frac{3}{4}\)
Amount of cups Freda will need to make four loaves of bread = 4 × \(\frac{9}{4}\)
= 1 × \(\frac{9}{1}\)
= 9.

Question 42.
What is \(\frac{1}{3}\) of 60%? ________
Answer:
\(\frac{1}{3}\) of 60% = \(\frac{1}{5}\)

Explanation:
\(\frac{1}{3}\) of 60%
= \(\frac{1}{3}\) ×  60%
= \(\frac{1}{3}\) × \(\frac{60}{100}\)
= \(\frac{1}{1}\) × \(\frac{20}{100}\)
= \(\frac{1}{1}\) × \(\frac{1}{5}\)
= \(\frac{1}{5}\)

Question 43.
What is 40% of \(\frac{3}{4}\)
in decimal form? ______________
in fraction form? _______________
Answer:
40% of \(\frac{3}{4}\)
in decimal form: 0.3
in fraction form: \(\frac{3}{10}\)

Explanation:
40% of \(\frac{3}{4}\)
= 40% × \(\frac{3}{4}\)
= \(\frac{40}{100}\) × \(\frac{3}{4}\)
= \(\frac{10}{100}\) × \(\frac{3}{1}\)
= \(\frac{1}{10}\) × \(\frac{3}{1}\)
= \(\frac{3}{10}\) or 0.3.

Question 44.
What are the perimeter and area of the figure?
Perimeter ____________________________
Area ______________________

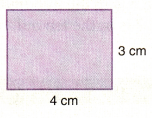
Answer:
Perimeter of the rectangle = 14 cm.
Area of the rectangle = 12 square cm.

Explanation:
Length of the rectangle = 4 cm.
Width of the rectangle = 3 cm.
Perimeter of the rectangle = 2 (Length of the rectangle + Width of the rectangle)
= 2(4 + 3)
= 2 × 7
= 14 cm.
Area of the rectangle = Length of the rectangle × Width of the rectangle
= 4 × 3
= 12 square cm.

Question 45.
One inch is equivalent to 2.54 centimeters. How many inches is 2.54 meters? How many centimeters are in loo inches?
______ inches = 2.54 meters 100 inches = __________ centimeters
Answer:
0.0254 inches = 2.54 meters 100 inches = 254 centimeters.

Explanation:
1 m = 100 cm
?? m = 2.54 cm
=> 2.54 × 1 = ?? × 100
=> 2.54 ÷ 100 = ??
=> 0.0254 inches.
1 inch = 2.54 centimeters.
100 inches = ?? centimeters
=> ?? = 2.54 × 100
=> ?? = 254 centimeters.

Question 46.
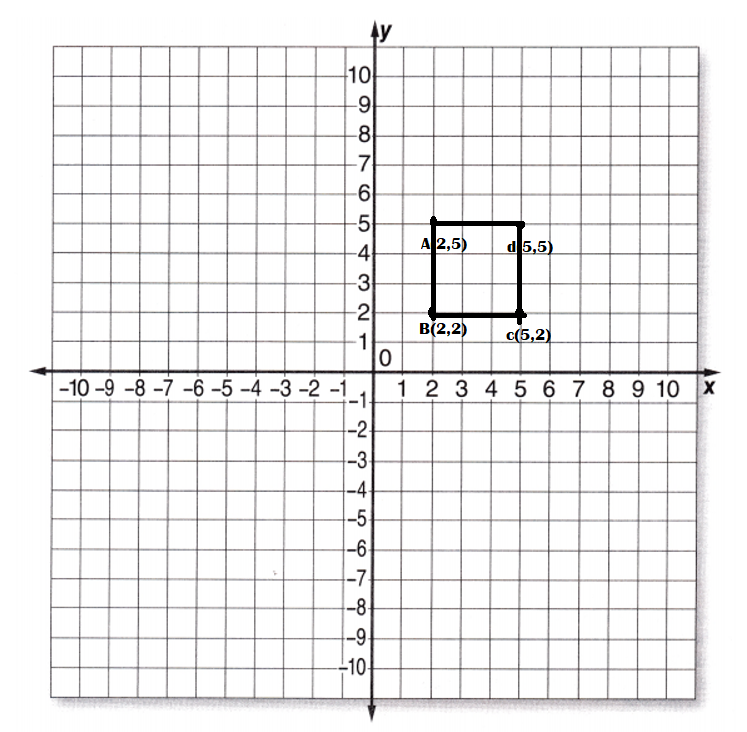
What figure is formed by connecting vertices at points A: (2, 5), B: (2, 2), C: (5, 2), and D: (5, 5) ?
What is the distance between points A and B? _______________________________________
Answer:
A square is formed by connecting vertices at points A: (2, 5), B: (2, 2), C: (5, 2), and D: (5, 5).
Distance between points A and B = 3.

Explanation:
vertices at points A: (2, 5), B: (2, 2), C: (5, 2), and D: (5, 5)

Distance between points A and B =

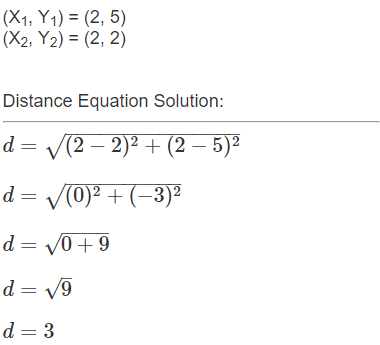
Question 47.
What are the volume and surface area of the figure?

Volume _____
Surface area ____
Answer:
Volume of the cuboid = 63.
Total Surface area of the cuboid = 109.

Explanation:
Length of the cuboid = 7
Width of the cuboid = 2
Height of the cuboid = 4.5
Volume of the cuboid = Length of the cuboid × Width of the cuboid × Height of the cuboid
= 7 × 2 × 4.5
= 14 × 4.5
= 63.
Total Surface area of the cuboid = 2 (length of the cuboid × Width of the cuboid) + 2(Width of the cuboid × height of the cuboid) + 2(length of the cuboid × height of the cuboid)
= 2(7 × 2) + 2(2 × 4.5) + 2(7 × 4.5)
= 2(14) + 2(9) + 2(31.5)
= 28 + 18 + 63
= 46 + 63
= 109.

Question 48.
Write an inequality to show that a number is greater than or equal to 10. _____
Answer:
The number must be 9 and above, to make x + 1  ≥ 10.

Explanation:
An inequality to show that a number is greater than or equal to 10:
Let the number be x.
=> x + 1  ≥ 10.
Let x must be 9 and above, to fulfill the equation.
=> x + 1 = 9 + 1 = 10.
=> x + 1 = 10 + 1 = 11.