McGraw Hill Math Grade 6 Posttest Answer Key

Practice questions available in McGraw Hill Math Grade 6 Answer Key PDF Posttest will engage students and is a great way of informal assessment.

McGraw-Hill Math Grade 6 Posttest Answer Key

Complete the following test items.

Question 1.
There are three hundred thousand, two hundred, fifty-two people living in Cincinnati. How would you write this number in standard form?
Answer:
Standard form of three hundred thousand, two hundred, fifty-two people living in Cincinnati = 33,252.

Explanation:
Number of people living in Cincinnati = three hundred thousand, two hundred, fifty-two people living in Cincinnati.
Standard form – 33000 + 200 + 52
=> 33,252.

Question 2.
Jerry is collecting newspapers for a recycling contest at his school. He needs 2,152 newspapers to win the contest. So far he has collected 1,375. Rounding to the nearest thousand, how many newspapers can we estimate that Jerry still needs to collect?
Answer:
Rounding to nearest thousand number of newspapers can we estimate that Jerry still needs to collect = 1,000.

Explanation:
Number of newspapers to win the contest he needs = 2,152.
Number of newspapers he collected = 1,375.
Rounding to nearest thousand:
Number of newspapers can we estimate that Jerry still needs to collect = Number of newspapers to win the contest he needs – Number of newspapers he collected
= 2,152 – 1,375
= 777.
Rounding to nearest thousand:
1000.

Calculate. Compare using <, >, or =
Question 3.

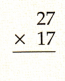
Answer:

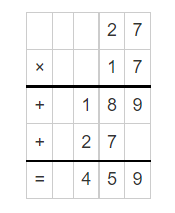
Explanation:
Multiplying 27 by 17, we get the product 459.

Question 4.

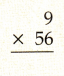
Answer:

Explanation:
Multiplying 9 by 56, we get the product 504.

Question 5.
|-14| __________ |14|
Answer:
|-14| = |14|

Explanation:
|-14| = 14.
|14| = 14.
=> Both are equal.

Question 6.
|-2| ___________ |-4|
Answer:
|-2| < |-4|

Explanation:
|-2| = 2.
|-4| = 4.
=> 2 is lesser than 4.

Question 7.
Marcia bought 13 apple pies for her class, but her classmates ate only half of each pie. How would Marcia express the amount of remaining apple pie as an improper fraction?
Answer:
Amount of remaining apple pie as an improper fraction = 6\(\frac{1}{2}\)

Explanation:
Number of apple pies for her class Marcia bought = 13.
But her classmates ate only half of each pie.
Number of apple pies left = 13 × \(\frac{1}{2}\)
= 6.5 or 6\(\frac{1}{2}\)

Calculate.
Question 8.

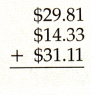
Answer:

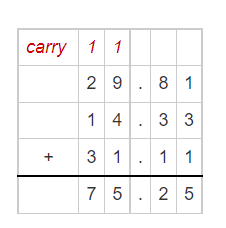
Explanation:
Sum of $29.81, $14.33 and $31.11, we get the $75.25.

Question 9.

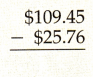
Answer:

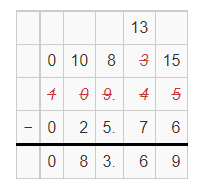
Explanation:
Subtraction of $109.45 and $25.76, we get $83.69.

Question 10.
What is the greatest common factor of 8 and 12?
Answer:
Greatest common factor of 8 and 12 is 4.

Explanation:
Greatest common factor of 8 and 12:
Factors of 8:
1,2,4,8.
Factors of 12:
1,2,3,4,6,12.

Question 11.
What is the least common multiple of 3 and 7?
Answer:
Least common multiple of 3 and 7 is 21.

Explanation:
Least common multiple of 3 and 7:
Multiples of 3:
3,6,9,12,15,18,21,24,27,30.
Multiples of 7:
7,14,21,28,35,42,49,56,63,70.

Question 12.
Ellen has been measuring the amount of snowfall for the last three months. She measured 1.262 inches in November, 1.794 inches in December, and 2.115 inches in January. Rounding to the nearest tenth of an inch, what was the total amount of snowfall during these three months?
Answer:
Total amount of snowfall during these three months = 5.171 inches.
Rounding to the nearest tenth of an inch, the total amount of snowfall during these three months = 10 inches.

Explanation:
Number of inches in November she measured = 1.262.
Number of inches in December she measured = 1.794.
Number of inches in January she measured = 2.115.
Total amount of snowfall during these three months = Number of inches in November she measured + Number of inches in December she measured + Number of inches in January she measured
= 1.262 + 1.794 + 2.115

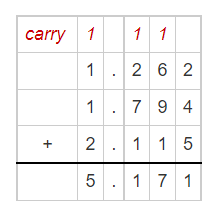
Rounding to the nearest tenth:
5.171 – 10 inches.

Calculate.
Question 13.

Answer:

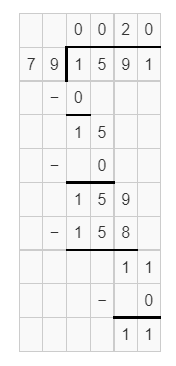
Explanation:
Dividing 1591 by 79, we get the quotient 20.13.

Question 14.

Answer:

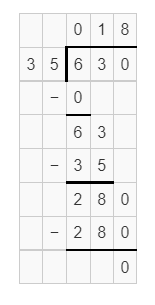
Explanation:
Dividing 630 by 35, we get the quotient 18.

Question 15.

Answer:

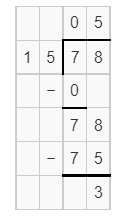
Explanation:
Dividing 78 by 15, we get the quotient 5.2.

Question 16.

Answer:

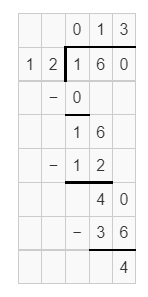
Explanation:
Dividing 160 by 12, we get the quotient 13.33.

Question 17.
Marvin is mixing the paint he will use to paint his living room. The directions to make 1 coat of paint call for him to mix 23.75 milliliters of black paint and 9.20 milliliters of white paint to achieve the correct shade of gray. How much black paint and how much white paint will he need in order to apply four coats of paint?
Answer:
Number of milliliters of black paint and white paint he needs to apply four coats of paint = 131.8.

Explanation:
Number of milliliters of black paint coat of paint call for him to mix = 23.75.
Number of milliliters of white paint to achieve the correct shade of gray = 9.20.
Number of milliliters of black paint and white paint he needs to apply four coats of paint = 4 (Number of milliliters of black paint coat of paint call for him to mix + Number of milliliters of  white paint to achieve the correct shade of gray)
= 4 (23.75 + 9.20)
= 4 × 32.95
= 131.8.

Question 18.
What is 40% of 150?
Answer:
40% of 150 = 60.

Explanation:
40% of 150 = \(\frac{40}{100}\) × 150
= \(\frac{40}{2}\) × 3
= \(\frac{20}{1}\) × 3
= 60.

Question 19.
What is 20% of \(\frac{4}{5}\)? Express the number in both decimal and fraction forms.
Answer:
20% of \(\frac{4}{5}\) = \(\frac{4}{25}\) or 0.16.

Explanation:
20% of \(\frac{4}{5}\) = \(\frac{20}{100}\) × \(\frac{4}{5}\)
= \(\frac{1}{5}\) × \(\frac{4}{5}\)
= \(\frac{4}{25}\) or 0.16.

Question 20.
Julia has a length of rope that is 17 \(\frac{1}{4}\) meters long. If 30 percent of the rope’s length has been painted blue, what length of the rope is not blue?
Answer:
Length of the rope is not blue = \(\frac{207}{40}\) or 5.175 meters.

Explanation:
Number of meters of rope that Julia has = 17 \(\frac{1}{4}\)
Length of the rope painted blue = 30%
Length of the rope is not blue = Number of meters of rope that Julia has × Length of the rope painted blue
= 17 \(\frac{1}{4}\) × 30%
= {[(17 × 4) + 1] ÷ 4} × 30%
= [(68 + 1) ÷ 4} × 30%
= \(\frac{69}{4}\) × \(\frac{30}{100}\)
= \(\frac{69}{2}\) × \(\frac{15}{100}\)
= \(\frac{69}{2}\) × \(\frac{3}{20}\)
= \(\frac{207}{40}\) or 5.175 meters.

Question 21.
Put the following decimals in order from least to greatest:
.0245, .06, .0003, .75, .029, .9, .0019, 3.084, .0925, .21
Answer:
Least to greatest:
0.003, 0.0019, 0.0245, 0.06, 0.21, 0.29, 0.75, 0.9, 0.925, 3.084.

Explanation:
0.9, 0.75, 0.21. 0.06, 0.29, 0.925, 0.003, 0.0019, 0.0245, 3.084.
Least to greatest:
0.003, 0.0019, 0.0245, 0.06, 0.21, 0.29, 0.75, 0.9, 0.925, 3.084.

Question 22.
Rob bought a scale that records weight digitally. His small luggage bag weighs 10.279 kilograms, his laptop bag weighs 15.653 kilograms, his clothing bag weighs 25.455 kilograms, and his large bag weighs 35.350 kilograms. What is the total weight of the four bags, in kilograms?
If a passenger is only allowed to carry 90 kilograms of luggage onto a flight, will Rob’s luggage exceed the limit?
Answer:
Total weight of the four bags = 86.737 kilograms.
No, Rob’s luggage will not exceed the limit because its lesser than 90 kilograms.

Explanation:
Number of kilograms his small luggage bag weighs = 10.279.
Number of kilograms his his laptop bag weighs = 15.653.
Number of kilograms his his clothing bag weighs = 25.455.
Number of kilograms his his large bag weighs = 35.350.
Total weight of the four bags = Number of kilograms his small luggage bag weighs + Number of kilograms his his laptop bag weighs + Number of kilograms his his clothing bag weighs + Number of kilograms his his large bag weighs
= 10.279 + 15.653 + 25.455 + 35.350
= 25.932 + 25.455 + 35.350
= 51.387 + 35.350
= 86.737 kilograms.

Question 23.

The chart shows how much time Brad and Simon spent practicing the clarinet last week. On which day did Brad practice for 95 minutes? _______________
On which day did Simon practice105 minutes longer than Brad? _______________
Answer:
Number of minutes brad spent on Thursday = 95.
Wednesday Simon practices 105 minutes longer than Brad.

Explanation:
Brad Practicing Time:
Number of minutes brad spent on Monday = 40.
Number of minutes brad spent on Tuesday = 110.
Number of minutes brad spent on Wednesday = 20.
Number of minutes brad spent on Thursday = 95.
Number of minutes brad spent on Friday = 25.
Simon Practicing Time:
Number of minutes Simon spent on Monday = 30.
Number of minutes Simon spent on Tuesday = 60.
Number of minutes Simon spent on Wednesday = 125.
Number of minutes Simon spent on Thursday = 75.
Number of minutes Simon spent on Friday = 30.
Difference:
Number of minutes Simon spent on Wednesday – Number of minutes brad spent on Wednesday
= 125 – 20
= 105.

Question 24.
Which city is colder in June? _______________
During which month is the difference in temperature the greatest? _______________
Answer:
Buenos Aires, Argentina city is colder in June.
During August month the difference in temperature the greatest.

Explanation:
Buenos Aires, Argentina temperature:
Temperature in June = 60°F
Temperature in July = 50°F
Temperature in August = 50°F
Temperature in September = 55°F
Seattle, Washington temperature:
Temperature in June = 70°F
Temperature in July = 75°F
Temperature in August = 80°F
Temperature in September = 70°F
Difference:
Seattle, Washington Temperature in August – Buenos Aires, Argentina Temperature in August
= 80°F – 50°F
= 30°F.
Seattle, Washington Temperature in June – Buenos Aires, Argentina Temperature in June
= 70°F – 60°F
= 10°F.
Seattle, Washington Temperature in July – Buenos Aires, Argentina Temperature in July
= 75°F – 50°F
= 25°F.
Seattle, Washington Temperature in September – Buenos Aires, Argentina Temperature in September
= 70°F – 55°F
= 15°F

Question 25.
Frank is looking at a solid figure that has two circular ends. It also has curved sides. What shape is he looking at?
Answer:
Frank is in look of a cylinder shape because it has two circular ends and curved sides.

Explanation:
Frank is looking at a solid figure that has two circular ends. It also has curved sides.
=> In mathematics, a cylinder is a three-dimensional solid that holds two parallel bases joined by a curved surface, at a fixed distance.

Question 26.
Tyler puts 5 nickels, 3 dimes, and 10 pennies into a hat. If you were to reach into that hat, what is the probability that you would pick a penny?
A dime? _______________
A nickel? _______________
Answer:
Probability that would pick a nickel penny = \(\frac{3}{18}\)
Probability that would pick a dime penny = \(\frac{5}{18}\)
Probability that would pick a pennies penny = \(\frac{10}{18}\)

Explanation:
Number of nickels Tyler puts into a hat = 5.
Number of dimes Tyler puts into a hat = 3.
Number of pennies Tyler puts into a hat = 10.
Total pennies he puts into a hat = Number of nickels Tyler puts into a hat + Number of dimes Tyler puts into a hat + Number of pennies Tyler puts into a hat
= 5 + 3 +10
= 8 + 10
= 18.
Probability that would pick a nickel penny = (Number of nickels Tyler puts into a hat ÷ Total pennies he puts into a hat)
= 5 ÷ 18
= \(\frac{5}{18}\)
Probability that would pick a dime penny = Number of dimes Tyler puts into a hat ÷ Total pennies he puts into a hat)
= 3 ÷ 18
= \(\frac{3}{18}\)
Probability that would pick a Pennies penny = Number of Pennies Tyler puts into a hat ÷ Total pennies he puts into a hat)
= 10 ÷ 18
= \(\frac{10}{18}\)

Question 27.
Which of the following triangles is

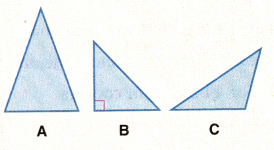
obtuse? _______________
right? _______________
acute? _______________
Answer:
Obtuse Triangle: C
Right Triangle: B
Acute Triangle: A

Explanation:
An obtuse triangle (or obtuse-angled triangle) is a triangle with one obtuse angle (greater than 90°) and two acute angles.
obtuse: C
A right-angled triangle is a type of triangle that has one of its angles equal to 90 degrees.
right: B
An acute triangle (or acute-angled triangle) is a  triangle with three acute angles (less than 90°).
acute: A

Question 28.
Calculate the following expression: 3 + (7 – 2)² + 4(5 + 3) – 6(6) = _____________
Answer:
3 + (7 – 2)² + 4(5 + 3) – 6(6) = 24.

Explanation:
3 + (7 – 2)² + 4(5 + 3) – 6(6)
= 3 + (7 – 2)² + 4(8) – 6(6)
= 3 + (5)² + 4(8) – 6(6)
= 3 + 25 + 4(8) – 6(6)
= 3 + 25 + 32 – 6(6)
= 3 + 25 + 32 – 36
= 28 + 32 – 36
= 60 – 36
= 24.

Question 29.
Write the following number using scientific notation: 2,345,836.0071.
Answer:
Scientific notation of 2,345,836.0071 = 2345836.71 x 10^-2.

Explanation:
A number is written in scientific notation when a number between 1 and 10 is multiplied by a power of 10.
2,345,836.0071 = 2345836.71 x 10^-2.

Question 30.
Michael collects postcards and state flags. His collection consists of 3 postcards and 1 flag from New Hampshire, 5 postcards and 2 flags from Florida, and 7 postcards from Ohio. If each postcard costs $.50 and each flag costs $4.50, how much did Michael spend for his collection?
Answer:
Amount of money Michael spend for his collection = $22.

Explanation:
Number of postcards from New Hampshire he collects = 3.
Number of flags from New Hampshire he collects = 1.
Number of postcards from Florida he collects = 5.
Number of flags from Florida he collects = 2.
Number of postcards from Ohio he collects = 7.
Total number of postcards he collects = Number of postcards from New Hampshire he collects + Number of postcards from Florida he collects + Number of postcards from Ohio he collects
= 3 + 5 + 7
= 10 + 7
= 17.
Total number of flags he collects = Number of flags from New Hampshire he collects + Number of postcards from Florida he collects
= 1 + 2
= 3.
Cost of each postcard = $.50
Cost of each flag = $4.50,
Amount of money Michael spend for his collection = (Total number of postcards he collects × Cost of each postcard) + (Total number of flags he collects × Cost of each flag)
= (17 × $0.50) + (3 × $4.50)
= $8.50 + $13.50
= $22.

Question 31.
Which of the following angles is

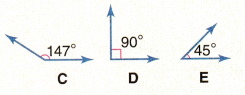
acute? _______________
right? _______________
obtuse? _______________
Answer:
Acute Triangle: E
Right Triangle: D
Obtuse Triangle: C

Explanation:
An acute triangle (or acute-angled triangle) is a  triangle with three acute angles (less than 90°).
acute: E
A right-angled triangle is a type of triangle that has one of its angles equal to 90 degrees.
right: D
An obtuse triangle (or obtuse-angled triangle) is a triangle with one obtuse angle (greater than 90°) and two acute angles.
obtuse: C

Question 32.
28 ÷ .25 = _____________
Answer:

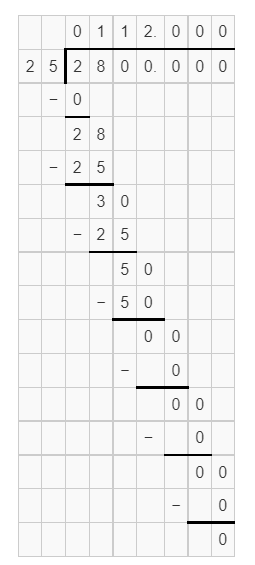
Explanation:
28 divided by 0.25, gives the quotient 112.

Question 33.
.3606 ÷ .06 = _____________
Answer:

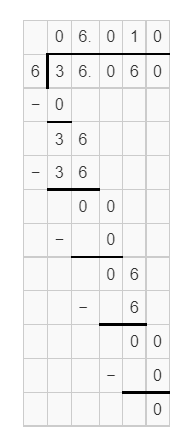
Explanation:
0.3606 divided by 0.06, gives the quotient 6.01.

Question 34.
What is \(\frac{22}{31}\) ÷ 7?
Answer:
\(\frac{22}{31}\) ÷ 7 = \(\frac{22}{217}\)

Explanation:
\(\frac{22}{31}\) ÷ 7
= \(\frac{22}{31}\) × \(\frac{1}{7}\)
= \(\frac{22}{217}\)

Question 35.
What is 18 ÷ \(\frac{4}{15}\)?
Answer:
18 ÷ \(\frac{4}{15}\) = 67 \(\frac{1}{2}\)

Explanation:
18 ÷ \(\frac{4}{15}\)
= 18 × \(\frac{15}{4}\)
= 9 × \(\frac{15}{2}\)
= \(\frac{135}{2}\)
= 67 \(\frac{1}{2}\)

Question 36.
What is \(\frac{38}{51}\) ÷ \(\frac{19}{17}\)?
Answer:
\(\frac{38}{51}\) ÷ \(\frac{19}{17}\) = \(\frac{2}{3}\)

Explanation:
\(\frac{38}{51}\) ÷ \(\frac{19}{17}\)
= \(\frac{38}{51}\) × \(\frac{17}{19}\)
= \(\frac{2}{51}\) × \(\frac{17}{1}\)
= \(\frac{2}{3}\) × \(\frac{1}{1}\)
= \(\frac{2}{3}\)

Question 37.
Latasha is in charge of providing bottled water and trail mix for her class field trip. Each student will be carrying \(\frac{3}{5}\) liters of water and \(\frac{1}{4}\) pound of trail mix during the trip. If there are 35 students on the trip, how much water and trail mix should Latasha bring for the class?
Answer:
Quantity of water and trail mix should Latasha bring for the class = 29\(\frac{3}{4}\)

Explanation:
Number of liters of water each student will be carrying = \(\frac{3}{5}\)
Number of pounds of trail mix each student will be carrying = \(\frac{1}{4}\)
Number of students = 35.
Quantity of water and trail mix should Latasha bring for the class = (Number of students × Number of liters of water each student will be carrying) + (Number of students × Number of pounds of trail mix each student will be carrying)
= (35 × \(\frac{3}{5}\)) + (35 × \(\frac{1}{4}\))
= (7 × \(\frac{3}{1}\)) + (35 × \(\frac{1}{4}\))
= \(\frac{21}{1}\) + \(\frac{35}{4}\)

Question 38.
Last week Matthew spent 5 \(\frac{1}{6}\) hours repairing his bike over a period of 3 \(\frac{1}{3}\) days. How many hours a day, on average, did Matthew spend working on his bike?
Answer:
Number of hours a day, on average, Matthew spend working on his bike = \(\frac{31}{20}\)

Explanation:
Number of hours repairing his bike last week Matthew spent = 5\(\frac{1}{6}\)
Number of days repairing his bike last week Matthew spent = 3\(\frac{1}{3}\)
Number of hours a day, on average, Matthew spend working on his bike = Number of hours repairing his bike last week Matthew spent  ÷ Number of days repairing his bike last week Matthew spent
= 5\(\frac{1}{6}\) ÷ 3\(\frac{1}{3}\)
= {[(5 × 6) + 1] ÷ 6} ÷ {[(3 × 3) + 1] ÷ 3}
= [(30 + 1) ÷ 6] ÷ [(9 + 1) ÷ 3]
= (31 ÷ 6) ÷ (10 ÷ 3)
= \(\frac{31}{6}\) ÷ \(\frac{10}{3}\)
= \(\frac{31}{6}\) × \(\frac{3}{10}\)
= \(\frac{31}{2}\) × \(\frac{1}{10}\)
= \(\frac{31}{20}\)

Question 39.
What is the decimal form of 9 \(\frac{3}{8}\)?
Answer:
Decimal form of 9 \(\frac{3}{8}\) = 9.375.

Explanation:
Decimal form of 9 \(\frac{3}{8}\) = {[(9 × 8) + 3] ÷ 8
= [(72 + 3) ÷ 8]
= (75 ÷ 8)
= 9.375.

Question 40.
What is the fraction form of 3.6?
Answer:
Fraction form of 3.6 = 7.2 ÷ 2.

Explanation:
Fraction form of 3.6:
3.6 × 2 = 7.2

Question 41.
Daniel is making chocolate chip cookies for his classmates at school. Each batch requires 3 \(\frac{2}{3}\) cups of sugar and \(\frac{1}{3}\) of a bag of chocolate chips. Create a ratio table to show the amounts Daniel will need to make 2, 3, or 4 batches of cookies.
Answer:

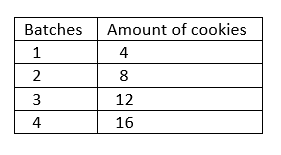
Explanation:
Number of cups of sugar each batch requires = 3\(\frac{2}{3}\)
Number of cups of of a bag of chocolate chips = \(\frac{1}{3}\)
Quantity of cups used to make each batch of cookies = Number of cups of sugar each batch requires + Number of cups of of a bag of chocolate chips
= 3\(\frac{2}{3}\) + \(\frac{1}{3}\)
= {[(3 × 3) + 2] ÷ 3} + \(\frac{1}{3}\)
= [(9 + 2) ÷ 3] + \(\frac{1}{3}\)
= \(\frac{11}{3}\) + \(\frac{1}{3}\)
= (11 + 1) ÷ 3
= 12 ÷ 3
= 4.
Quantity of cups used to make 2 batch of cookies = 2 × Quantity of cups used to make each batch of cookies
= 2 × 4
= 8.
Quantity of cups used to make 3 batch of cookies = 3 × Quantity of cups used to make each batch of cookies
= 3 × 4
= 12.
Quantity of cups used to make 4 batch of cookies = 4 × Quantity of cups used to make each batch of cookies
= 4 × 4
= 16.

Question 42.
What is \(\frac{1}{3}\) of 72%?
Answer:
\(\frac{1}{3}\) of 72% = \(\frac{6}{25}\)

Explanation:
\(\frac{1}{3}\) of 72%
= \(\frac{1}{3}\) × \(\frac{72}{100}\)
= \(\frac{1}{1}\) × \(\frac{24}{100}\)
= \(\frac{1}{1}\) × \(\frac{12}{50}\)
= \(\frac{1}{1}\) × \(\frac{6}{25}\)
= \(\frac{6}{25}\)

Question 43.
What is 60% of \(\frac{1}{4}\)
in decimal form? _____________
in fraction form? _____________
Answer:
60% of \(\frac{1}{4}\)
in decimal form – 0.15.
in fraction form – \(\frac{3}{20}\)

Explanation:
60% of \(\frac{1}{4}\)
= 60% × \(\frac{1}{4}\)
= \(\frac{60}{100}\) × \(\frac{1}{4}\)
= \(\frac{6}{10}\) × \(\frac{1}{4}\)
= \(\frac{3}{10}\) × \(\frac{1}{2}\)
= \(\frac{3}{20}\)
= 0.15.

Question 44.
What are the perimeter and area of the figure?

Perimeter _____________________
Area __________________
Answer:
Perimeter – 24 cm.
Area – 35 square cm.

Explanation:
Length of the rectangle =  7cm.
Width of the rectangle =  5cm.
Perimeter of the rectangle = 2(Length of the rectangle + Width of the rectangle)
= 2(7 + 5)
= 2 × 12
= 24 cm.
Area of the rectangle = Length of the rectangle × Width of the rectangle
= 7 × 5
= 35 square cm.

Question 45.
One inch is equivalent to 2.54 centimeters. How many inches is 4 meters? How many centimeters are in 254 inches?
__________ inches = 4 meters
254 inches = __________ centimeters
Answer:
157.48 inches = 4 meters.
254 inches = 645.16 centimeters.

Explanation:
One inch = 2.54 centimeters.
1 meter = 100 centimeters.
=> One inch × 100 = 2.54 × 1
=> One inch = 2.54 ÷ 100
=> One inch = 0.0254 meters.
4 meters = One inch × 4 = 0.0254 × ??
=> 1 × 4 ÷ 0.0254 = ??
=> 157.48 inches.
One inch = 2.54 centimeters.
254 inches = ?? centimeters
=> ?? × 1 = 2.54 × 254
=> ?? = 645.16 centimeters.

Question 46.
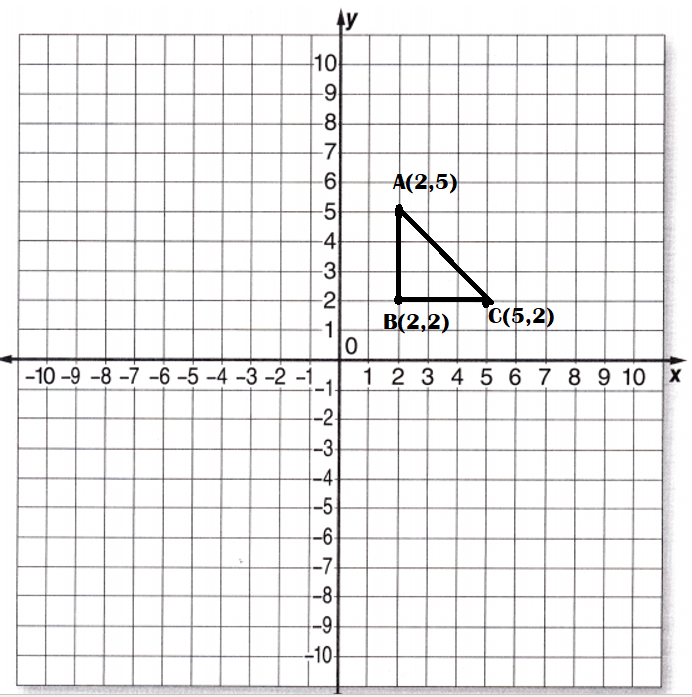
What figure is formed by connecting vertices at points A: (2, 5), B: (2, 2), and C: (5, 2)?
What is the distance between points A and B?
Answer:
Distance between points A and B:

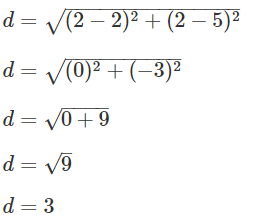
Figured formed is a triangle by point A: (2, 5), B: (2, 2), and C: (5, 2).

Explanation:
Vertices at points A: (2, 5), B: (2, 2), and C: (5, 2)
Figure formed :

Question 47.
What are the volume and surface area of the figure?

Volume _____________
Surface area ______________
Answer:
Volume – 52.
Surface area – 94.

Explanation:
Length of the cuboid = 6.5.
Breadth of the cuboid = 2.
Height of the cuboid = 4.
Volume of the cuboid = Length of the cuboid × Breadth of the cuboid × Height of the cuboid
= 6.5 × 2 × 4
= 13 × 4
= 52.
Total Surface area of cuboid = 2 (length × breadth) + 2(breadth × height) + 2(length × height)
= 2(6.5 × 2) + 2(2 × 4) + 2(6.5 × 4)
= 2(13) + 2(8) + 2(26)
= 26 + 16 + 52
= 42 + 52
= 94.

Question 48.
Write an inequality to show that a number is less than or equal to 7.
Answer:
Inequality to show that a number is less than or equal to 7:
x + 1 ≤ 7

Explanation:
Inequality to show that a number is less than or equal to 7:
To show inequality of numbers, let the number be x and less than 7.
=> x < 7.
Add 1:
x + 1 ≤ 7