Practice questions available in McGraw Hill Math Grade 6 Answer Key PDF Lesson 6.6 Adding Mixed Numbers with Unlike Denominators will engage students and is a great way of informal assessment.
McGraw-Hill Math Grade 6 Answer Key Lesson 6.6 Adding Mixed Numbers with Unlike Denominators
Exercises Add
Question 1.
1\(\frac{2}{3}\) + 3\(\frac{1}{5}\)
Answer:
1\(\frac{2}{3}\) + 3\(\frac{1}{5}\) = 4\(\frac{13}{15}\)
Explanation:
1\(\frac{2}{3}\) + 3\(\frac{1}{5}\)
= {[(1× 3) + 2] ÷ 3} + {[(3 × 5) + 1] ÷ 5}
= [(3 + 2) ÷ 3] + [(15 + 1) ÷ 5]
= \(\frac{5}{3}\) + \(\frac{16}{5}\)

Question 2.
4\(\frac{1}{7}\) + 3\(\frac{3}{5}\)
Answer:
4\(\frac{1}{7}\) + 3\(\frac{3}{5}\) = 7\(\frac{26}{35}\)
Explanation:
4\(\frac{1}{7}\) + 3\(\frac{3}{5}\)
= {[(4 × 7) + 1] ÷ 7} + {[(3 × 5) + 3] ÷ 5}
= [(28 + 1) ÷ 7] + [(15 + 3) ÷ 5]
= (29 ÷ 7) + (18 ÷ 5)
= 
Question 3.
5\(\frac{1}{9}\) + 2\(\frac{3}{7}\)
Answer:
5\(\frac{1}{9}\) + 2\(\frac{3}{7}\) = 7\(\frac{34}{63}\)
Explanation:
5\(\frac{1}{9}\) + 2\(\frac{3}{7}\)
= {[(5 × 9) + 1] ÷ 9} + {[(2 × 7) + 3] ÷ 7}
= [(45 + 1) ÷ 9] + [(14 + 3) ÷ 7]
= (46 ÷ 9) + (17 ÷ 7)

Question 4.
1\(\frac{2}{3}\) + 4\(\frac{1}{16}\)
Answer:
1\(\frac{2}{3}\) + 4\(\frac{1}{16}\) = 5\(\frac{35}{48}\)
Explanation:
1\(\frac{2}{3}\) + 4\(\frac{1}{16}\)
= {[(1 × 3) + 2] ÷ 3} + {[(4 × 16) + 1] ÷ 16}
= [(3 + 2) ÷ 3] + [(64 + 1) ÷ 16]
= (5 ÷ 3) + (65 ÷ 16)

Question 5.
10\(\frac{3}{7}\) + 2\(\frac{3}{11}\)
Answer:
10\(\frac{3}{7}\) + 2\(\frac{3}{11}\) = 12\(\frac{54}{77}\)
Explanation:
10\(\frac{3}{7}\) + 2\(\frac{3}{11}\)
= {[(10 × 7) + 3] ÷ 7} + {[(2 × 11) + 3] ÷ 11}
= [(70 + 3) ÷ 7] + [(22 + 3) ÷ 11]
= (73 ÷ 7) + (25 ÷ 11)

Question 6.
3\(\frac{1}{4}\) + 5\(\frac{2}{9}\)
Answer:
3\(\frac{1}{4}\) + 5\(\frac{2}{9}\) = 8\(\frac{17}{36}\)
Explanation:
3\(\frac{1}{4}\) + 5\(\frac{2}{9}\)
= {[(3 × 4) + 1] ÷ 4} + {[(5 × 9) + 2] ÷ 9}
= [(12 + 1) ÷ 4] + [(45 + 2) ÷ 9]
= (13 ÷ 4) + (47 ÷ 9)
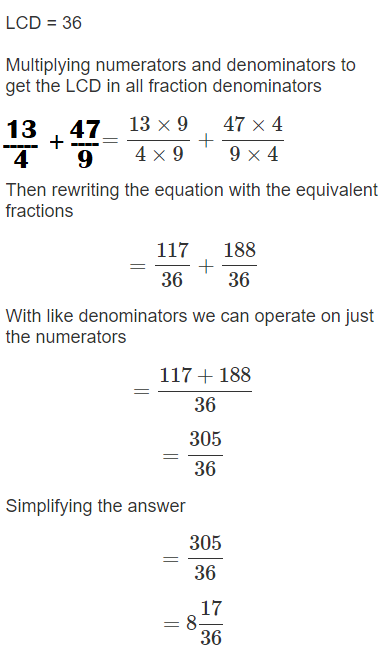
Question 7.
11\(\frac{2}{7}\) + 12\(\frac{3}{8}\)
Answer:
11\(\frac{2}{7}\) + 12\(\frac{3}{8}\) = 23\(\frac{37}{56}\)
Explanation:
11\(\frac{2}{7}\) + 12\(\frac{3}{8}\)
= {[(11 × 7) + 2] ÷ 7} + {[(12 × 8) + 3] ÷ 8}
= [(77 + 2) ÷ 7] + [(96 + 3) ÷ 8]
= (79 ÷ 7) + (99 ÷ 8)

Question 8.
12\(\frac{5}{6}\) + 1\(\frac{1}{15}\)
Answer:
12\(\frac{5}{6}\) + 1\(\frac{1}{15}\) = 13\(\frac{9}{10}\)
Explanation:
12\(\frac{5}{6}\) + 1\(\frac{1}{15}\)
= {[(12 × 6) + 5] ÷ 6} + {[(1 × 15) + 1] ÷ 15}
= [(72 + 5) ÷ 6] + [(15 + 1) ÷ 15]
= (77 ÷ 6) + (16 ÷ 15)

Question 9.
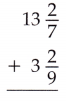
Answer:
13\(\frac{2}{7}\) + 3\(\frac{2}{9}\) = 16\(\frac{32}{63}\)
Explanation:
13\(\frac{2}{7}\) + 3\(\frac{2}{9}\)
= {[(13 × 7) + 2] ÷ 7} + {[(3 × 9) + 2] ÷ 9}
= [(91 + 2) ÷ 7] + [(27 + 2) ÷ 9]
= (93 ÷ 7) + (29 ÷ 9)
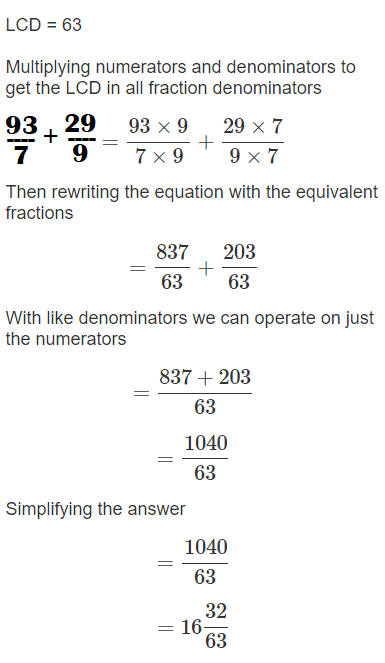
Question 10.
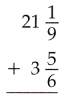
Answer:
21\(\frac{1}{9}\) + 3\(\frac{5}{6}\) = 15\(\frac{17}{18}\)
Explanation:
21\(\frac{1}{9}\) + 3\(\frac{5}{6}\)
= {[(21 × 9) + 1] ÷ 9} + {[(3 × 6) + 5] ÷ 6}
= [(108 + 1) ÷ 9] + [(18 + 5) ÷ 6]
= (109 ÷ 9) + (23 ÷ 6)

Question 11.
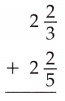
Answer:
2\(\frac{2}{3}\) + 2\(\frac{2}{5}\) = 5\(\frac{1}{15}[/latex
Explanation:
2[latex]\frac{2}{3}\) + 2\(\frac{2}{5}\)
= {[(2 × 3) + 2] ÷ 3} + {[(2 × 5) + 2] ÷ 5}
= [(6 + 2) ÷ 3] + [(10 + 2) ÷ 5]
= (8 ÷ 3) + (12 ÷ 5)

Question 12.
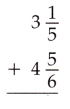
Answer:
3\(\frac{1}{5}\) + 4\(\frac{5}{6}\) = 8\(\frac{1}{30}\)
Explanation:
3\(\frac{1}{5}\) + 4\(\frac{5}{6}\)
= {[(3 × 5) + 1] ÷ 5} + {[(4 × 6) + 5] ÷ 6}
= [(15 + 1) ÷ 5] + [(24 + 5) ÷ 6]
= (16 ÷ 5) + (29 ÷ 6)

Question 13.
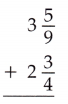
Answer:
3\(\frac{5}{9}\) + 2\(\frac{3}{4}\) = 6\(\frac{11}{36}\)
Explanation:
3\(\frac{5}{9}\) + 2\(\frac{3}{4}\)
= {[(3 × 9) + 5] ÷ 9} + {[(2 × 4) + 3] ÷ 4}
= [(27 + 5) ÷ 9] + [(8 + 3) ÷ 4]
= (32 ÷ 9) + (11 ÷ 4)

Question 14.
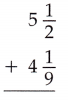
Answer:
5\(\frac{1}{2}\) + 4\(\frac{1}{9}\) = 9\(\frac{11}{18}\)
Explanation:
5\(\frac{1}{2}\) + 4\(\frac{1}{9}\)
= {[(5 × 2) + 1] ÷ 2} + {[(4 × 9) + 1] ÷ 9}
= [(10 + 1) ÷ 2] + [(36 + 1) ÷ 9]
= (11 ÷ 2) + (37 ÷ 9)

Question 15.
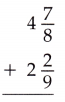
Answer:
4\(\frac{7}{8}\) + 2\(\frac{2}{9}\) = 7\(\frac{7}{72}\)
Explanation:
4\(\frac{7}{8}\) + 2\(\frac{2}{9}\)
= {[(4 × 8) + 7] ÷ 8} + {[(2 × 9) + 2] ÷ 9}
= [(32 + 7) ÷ 8] + [(18 + 2) ÷ 9]
= (39 ÷ 8) + (20 ÷ 9)

Question 16.
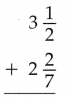
Answer:
3\(\frac{1}{2}\) + 2\(\frac{2}{7}\) = 5\(\frac{11}{14}\)
Explanation:
3\(\frac{1}{2}\) + 2\(\frac{2}{7}\)
= {[(3 × 2) + 1] ÷ 2} + {[(2 × 7) + 2] ÷ 7}
= [(6 + 1) ÷ 2] + [(14 + 2) ÷ 7]
= (7 ÷ 2) + (16 ÷ 7)
