Practice questions available in McGraw Hill Math Grade 6 Answer Key PDF Lesson 18.5 Area will engage students and is a great way of informal assessment.
McGraw-Hill Math Grade 6 Answer Key Lesson 18.5 Area
Exercises
SOLVE
Question 1.
What is the area of a square with 4 ft sides?
Answer:
Area of square = 16 square feet.
Explanation:
Side of square = 4 feet.
Area of square = Side of square × Side of square
= 4 × 4
= 16 square feet.
Question 2.
If a rectangle has sides of 2 ft and 12 ft, what is its area?
Answer:
Area of a rectangle = 24 square feet.
Explanation:
Length of a rectangle = 12 feet.
Width of a rectangle = 2 feet.
Area of a rectangle = Length of a rectangle × Width of a rectangle
= 12 × 2
= 24 square feet.
Question 3.
There are 9 sq ft in one square yard (3 ft × 3 ft). How many square feet are in a 3-yd by 4-yd rug?
Answer:
Area of the rug = 12 square yards.
Explanation:
Length of the rug = 3-yd
Width of the rug = 4-yd
Area of the rug = Length of the rug × Width of the rug
= 3 yards × 4 yards
= 12 square yards.
Question 4.
How much will the area decrease if you take away 3 feet from each side of a square with 10-ft long sides?
Answer:
91 square feet the area decrease if you take away 3 feet from each side of a square with 10-ft long sides.
Explanation:
Side of square = 3 feet.
Area of square = Side of square × Side of square
= 3 feet × 3 feet
= 9 square feet.
Side of square = 10 feet.
Area of square = Side of square × Side of square
= 10 feet × 10 feet
= 100 square feet.
Difference:
= 100 square feet – 9 square feet
= 91 square feet.
Question 5.
John walks west 20 ft, then 10 ft to the south, then 20 ft to the east, and then returns to his starting point to form a rectangle. What is the area of that rectangle?
Answer:
Area of the rectangle = 60 square feet.
Explanation:
Number of feet John walks to the west = 20 feet.
Number of feet John walks to the south = 10 feet.
Number of feet John walks to the east = 20 feet.
Number of feet John walks to the north = 10 feet
Area of the rectangle = Number of feet John walks to the west + Number of feet John walks to the south + Number of feet John walks to the east + Number of feet John walks to the north
= 20 feet + 10 feet + 20 feet + 10 feet
= 30 feet + 20 feet + 10 feet
= 50 feet + 10 feet
= 60 square feet.
Question 6.
If a square that has sides of 25 ft is split in half, what is the area of each of the pieces?
Answer:
Area of each of the pieces = 156.25 square feet.
Explanation:
If a square that has sides of 25 ft is split in half.
=> Side of the square = 25 feet ÷ 2
= 12.5 feet.
Area of each of the pieces = Side of the square × Side of the square
= 12.5 × 12.5
= 156.25 square feet.
Question 7.
A right triangle has sides of 7 ft, 24 ft, and 25 ft. What is its area?
Answer:
Area of a right triangle = 84 square feet.
Explanation:
Sides of a right triangle = 7 ft, 24 ft, and 25 ft.
Area of a right triangle = \(\frac{1}{2}\) × Base × Height
= \(\frac{1}{2}\) × 7 feet × 24 feet
= 7 feet × 12 feet
= 84 square feet.
Question 8.
Which has a larger area, a triangle with a base of 15 ft and a height 25 ft or a square with sides of 14 ft?
Answer:
Area of a square has a larger area than a triangle with a base of 15 ft and a height 25 ft.
Explanation:
Base of the triangle = 15 feet.
Height of triangle = 25 feet.
Area of the triangle = \(\frac{1}{2}\) × Base × Height
= \(\frac{1}{2}\) × 15 feet × 25 feet
= \(\frac{375}{2}\)
= 187.5 square feet.
Side of a square = 14 feet.
Area of a square = Side of a square × Side of a square
= 14 feet × 14 feet
= 196 square feet.
Question 9.
What is the area of a rectangle that is 3.2 inches by 4.8 inches?
Answer:
Area of the rectangle = 15.36 square inches.
Explanation:
Length of the rectangle = 4.8 inches
Width of the rectangle = 3.2 inches.
Area of the rectangle = Length of the rectangle × Width of the rectangle
= 4.8 × 3.2
= 15.36 square inches.
Question 10.

Answer:
Area of the rectangle = 15.
Explanation:
Length of the rectangle = 7.5.
Width of the rectangle = 2.
Area of the rectangle = Length of the rectangle × Width of the rectangle
= 7.5 × 2
= 15.
Question 11.
Kim wants to put carpet on her bedroom floor and needs to find the total area of the floor. If the floor measures 13.5 feet by 12 feet, what is the total area of the floor?
Answer:
Total area of the floor = 162 square feet.
Explanation:
Length of the floor = 13.5 feet.
Width of the floor = 12 feet.
Total area of the floor = Length of the floor × Width of the floor
= 13.5 feet × 12 feet
= 162 square feet.
Question 12.
What is the area of a square with sides of .7 inches?
Answer:
Area of the square = 0.49 square inches.
Explanation:
Side of the square = 0.7 inches.
Area of the square = Side of the square × Side of the square
= 0.7 × 0.7
= 0.49 square inches.
Question 13.
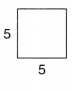
Answer:
Area of the square = 25.
Explanation:
Side of the square = 5.
Area of the square = Side of the square × Side of the square
= 5 × 5
= 25.
Question 14.
If Aaron wants to lay a tile floor in a room that is 12 feet long and 9 feet wide, how 5 many 1 ft. square tiles will he need?
Answer:
Area of the tile floor = 108 square feet.
Explanation:
Length of the tile floor = 12 feet.
Width of the tile floor = 9 feet.
Area of the tile floor = Length of the tile floor × Width of the tile floor
= 12 feet × 9 feet.
= 108 square feet.
Question 15.
What is the area of a triangle with base and height 5cm?
Answer:
Area of the triangle = 12.5 square cm.
Explanation:
Base of the triangle = 5 cm.
Height of the triangle = 5 cm.
Area of the triangle = \(\frac{1}{2}\) × Base of the triangle × Height of the triangle
= \(\frac{1}{2}\) × 5 × 5
= \(\frac{1}{2}\) × 25
= 12.5 square cm.
Question 16.
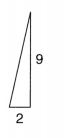
Answer:
Area of the triangle = 9.
Explanation:
Base of the triangle = 2.
Height of the triangle = 9.
Area of the triangle = \(\frac{1}{2}\) × Base of the triangle × Height of the triangle
= \(\frac{1}{2}\) × 2 × 9
= 9.
Question 17.
A sailboat has a triangular sail with an area of 12 ft2. If the height of the sail is 6 feet, how long is the base?
Answer:
Area of the triangle = 4 feet.
Explanation:
Area of the triangular sail = 12 ft2.
Height of the triangular sail = 6 feet.
Base of the triangular sail = ?? feet.
Area of the triangle = \(\frac{1}{2}\) × Base of the triangle × Height of the triangle
=> 12 square feet = \(\frac{1}{2}\) × Base of the triangle × 6 feet
=> 12 square feet = Base of the triangle × 3 feet
=> 12 ÷ 3 = Base of the triangle
=> 4 feet = Base of the triangle
Question 18.
What is the area of the figure below?
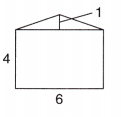
Answer:
Total area of the figure = 27.
Explanation:
Length of the rectangle = 6.
Width of the rectangle = 4.
Area of the rectangle = Length of the rectangle × Width of the rectangle
= 6 × 4
= 24.
Base of the triangle = 6.
Height of the triangle = 1.
Area of the triangle = \(\frac{1}{2}\) × Base of the triangle × Height of the triangle
= \(\frac{1}{2}\) × 6 × 1
= 3.
Total area of the figure = Area of the rectangle + Area of the triangle
= 24 + 3
= 27.
Question 19.
Erlene needs 5 square feet of fabric to make a jacket. If she buys a square of blue fabric that is 2 feet long and 2 feet wide and a triangular piece of red fabric for the hood that measures 2 feet across the base and is 1 foot high, will she have enough fabric?
Answer:
Area of the square of blue fabric = 4 square feet.
Explanation:
Area of the fabric to make a jacket Erlene needs = 5 square feet.
Side of the square of blue fabric = 2 feet.
Area of the square of blue fabric = Side of the square of blue fabric × Side of the square of blue fabric
= 2 feet × 2 feet
= 4 square feet.
Question 20.
The total area of a square is 9 inches2. If the square is cut in half diagonally, what is the area of one of the triangles?
Answer:
Area of a triangle = 4.5 Square units.
Explanation:
Total area of a square = 9 square inches.
Side of a square = √9 = 3 units.
Base of the triangle = 3 units.
Height of the triangle = 3 units.
Area of a triangle = \(\frac{1}{2}\) × Base of the triangle × Height of the triangle
= \(\frac{1}{2}\) × 3 × 3
= \(\frac{1}{2}\) × 9
= 4.5 Square units.