All the solutions provided in McGraw Hill Math Grade 5 Answer Key PDF Chapter 11 Test are as per the latest syllabus guidelines.
McGraw-Hill Math Grade 5 Chapter 11 Test Answer Key
This line plot shows the height in meters of seven young orange trees.

Question 1.
Which height is an outlier?
Answer:
The height 3\(\frac{2}{10}\) m or 3\(\frac{1}{5}\) m is an outlier.
Question 2.
How many trees have a height of 3\(\frac{7}{10}\) m?
Answer:
Two trees have a height of 3\(\frac{7}{10}\) m.
Question 3.
What is the most common height in the data set?
Answer:
The most common height in the given data set is 3\(\frac{8}{10}\) m or 3\(\frac{4}{5}\) m.
Question 4.
What is the total height of the three shortest trees?
Answer:
The height of first shortest tree is 3\(\frac{2}{10}\) m.
The height of second and third shortest tree is 3\(\frac{7}{10}\) m.
= 3\(\frac{2}{10}\) m + 3\(\frac{7}{10}\) m + 3\(\frac{7}{10}\) m
= \(\frac{32}{10}\) m + \(\frac{37}{10}\) m + \(\frac{37}{10}\) m
= \(\frac{106}{10}\) m
=10 \(\frac{6}{10}\) m or 10 \(\frac{3}{5}\) m
The total height of the three shortest trees is 10\(\frac{6}{10}\) m or 10\(\frac{3}{5}\) m.
Question 5.
What is the difference between the tallest tree and the shortest tree shown on the line plot?
Answer:
The tallest tree on the line plot is 3\(\frac{9}{10}\) m.
The shortest tree on the line plot is 3\(\frac{2}{10}\) m.
= 3\(\frac{9}{10}\) m – 3\(\frac{2}{10}\) m
= \(\frac{39}{10}\) m – \(\frac{32}{10}\) m
= \(\frac{7}{10}\) m
The difference between the tallest tree and the shortest tree is \(\frac{7}{10}\) m.
Question 6.
To find the average height, you would find the sum of all the heights shown and then divide by the number of trees. What is the average height shown on the line plot?
Answer:
The height of seven young orange trees is as below,
= 3\(\frac{2}{10}\) m + 2(3\(\frac{7}{10}\))m + 3(3\(\frac{8}{10}\)) m + 3\(\frac{9}{10}\))m
= \(\frac{32}{10}\) m + 2 (\(\frac{37}{10}\)) m + 3(\(\frac{38}{10}\)) m + \(\frac{39}{10}\) m
= \(\frac{32}{10}\) m + \(\frac{74}{10}\) m +\(\frac{114}{10}\) m + \(\frac{39}{10}\) m
= \(\frac{259}{10}\) m
The sum of all the heights of seven young orange trees is \(\frac{259}{10}\) m.
The total number of trees are seven.
The average height shown on the line plot = Sum of all the heights of seven young oranges trees/ Total number of trees
= \(\frac{259}{10}\) m/ 7
= 3.7 m
= 3\(\frac{7}{10}\) m
The average height shown on the line plot is 3\(\frac{7}{10}\) m.
Plot and label each point on the coordinate grid.
Question 7.
A (2, 3)
Answer:
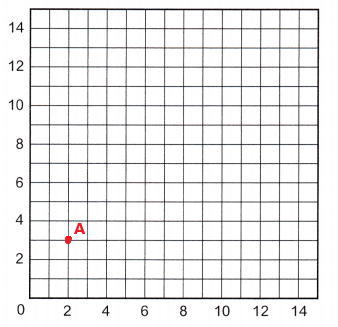
The point A (2, 3) is plotted and labeled on the grid.
Question 8.
B (6, 4)
Answer:
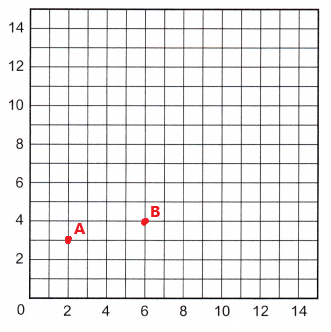
The point B (6, 4) is plotted and labeled on the grid.
Question 9.
C (4, 8)
Answer:

The point C (4, 8) is plotted and labeled on the grid.
Question 10.
D (7, 13)
Answer:
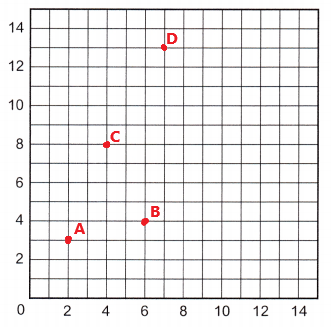
The point D (7, 13) is plotted and labeled on the grid.
Question 11.
E (10, 10)
Answer:
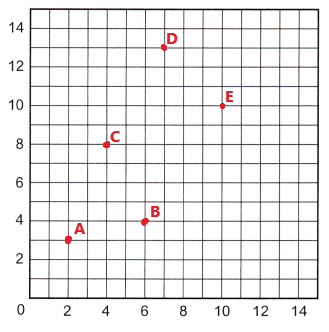
The point E (10, 10) is plotted and labeled on the grid.
Plot each point. Draw lines between the points. Identify the shape.

Question 12.
A (8, 11)
B (2, 2)
C (14, 2)
Identify the shape.
Answer:

Explanation:
After plotting and joining the given set of points we can see that a triangle having three equal sides. So, this is a equilateral triangle.
Plot each point. Draw lines between the points. Identify the shape.

Question 13.
A (2, 4)
B (2, 10)
C (8, 10)
D (8, 4)
Identify the shape.
Answer:
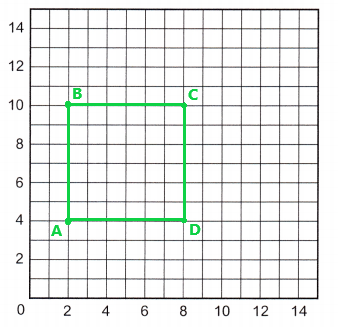
Explanation:
After plotting and joining the given set of points we can see that a quadrilateral having four equal sides. So, this is a Square.