Practice the questions of McGraw Hill Math Grade 4 Answer Key PDF Chapter 8 Test to secure good marks & knowledge in the exams.
McGraw-Hill Math Grade 4 Chapter 8 Test Answer Key
Add or subtract. Write your answers in simplest form.
Question 1.

Answer:
The Denominators of the given fractions are same so add the numerators.
3/5 + 1/5
= 3 + 1/5
= 4/5.
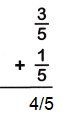
Question 2.

Answer:
The Denominators of the given fractions are same so add the numerators.
1/8 + 5/8
= 6/8
= 3/4.
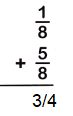
Question 3.
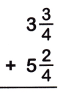
Answer:
3 x (3/4) = 15/4
5 x (2/4) = 22/4 = 11/2
Here the denominators are not equal. so, 15/4 + 11/2
= (15 x 2) + (11 x 4) ÷ 4 x 2
= 30+44/8
= 74/8
The 74/8 can be written has 9 x 1/4

Question 4.
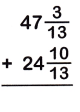
Answer:
47 x (3/13) = 614/13
24 x (10/13) = 322/13
The Denominators of the given fractions are same so add the numerators.
614/13 + 322/13 = 72
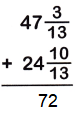
Question 5.
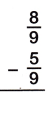
Answer:
The Denominators of the given fractions are same so subtract the numerators.
8/9 – 5/9
= 8-5/9
= 3/9
= 1/3
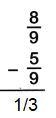
Question 6.
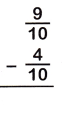
Answer:
The Denominators of the given fractions are same so subtract the numerators.
9/10 – 4/10
= 9-4/10
= 5/10
= 1/2
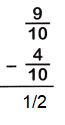
Question 7.

Answer:
9 x (5/6) = 59/6
7 x (3/6) = 45/6
The Denominators of the given fractions are same so subtract the numerators.
59/6 – 45/6
= 59-45/6
= 14/6
= 7/3
7/3 can be written as 2 x 1/3.
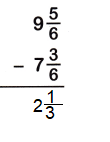
Question 8.
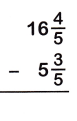
Answer:
5 x (3/5) = 54/5
16 x (4/5) =28/5
The Denominators of the given fractions are same so subtract the numerators.
54/5 – 28/5
= 54-28/5
= 26/5
26/5 can be written has 5 x 1/5
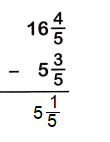
Question 9.
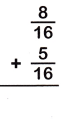
Answer:
The Denominators of the given fractions are same so add the numerators.
8/16 + 5/16
= 8+5/16
= 13/16
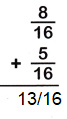
Question 10.
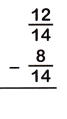
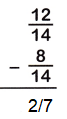
Answer:
The Denominators of the given fractions are same so subtract the numerators.
12/14 – 8/14
= 12-8/14
= 4/14
= 2/7
Question 11.
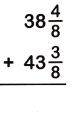
Answer:
38 x (4/8) = 308/8
43 x (3/8) = 347/8
The Denominators of the given fractions are same so add the numerators.
308/8 + 347/8
= 308+347/8
= 655/8
= 81 x 7/8
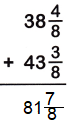
Question 12.
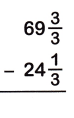
Answer:
69 x (3/3) = 210/3
24 x (1/3) = 73/3
The Denominators of the given fractions are same so subtract the numerators.
210/3 – 73/3
= 210-73/3
= 137/3
= 45 x 2/3
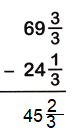
Solve. Write your answers in simplest form.
Question 13.
A family bought apples at a farmer’s market. They bought a bag of red apples that weighed 7\(\frac{4}{8}\) pounds and a bag of green apples that weighed 3\(\frac{3}{8}\) pounds on Saturday. How many pounds of apples did they buy?
Answer:
The family bought a bag of red apples = 7 x (4/8) pounds = 60/8
The family bought a bag of green apples = 3 x (3/8) pounds = 27/8
The Denominators of the given fractions are same so add the numerators.
60/8 + 27/8 = 60-27/8
= 87/8
= 10 x 7/8
Hence, the total number of apples that the family bought is 2 x (7/8) pounds.
Question 14.
Alex makes a salad for the family. He uses 4\(\frac{2}{9}\) cups of lettuce, 1\(\frac{1}{9}\) cups of tomatoes, and 2\(\frac{4}{9}\) cups of cucumbers. How many more cups of lettuce does he use than cucumbers?
Answer:
Given that,
The total number of lettuce cups = 4 x (2/9) cups = 38/9.
The total number of tomato cups = 1 x (1/9) cups = 10/9.
The total number of cucumber cups = 2 x (4/9) cups = 22/9.
Therefore the lettuce cups more than cucumber cups is 38/9 – 22/9
The Denominators of the given fractions are same so subtract the numerators.
= 38-22/9
= 16/9
= 1 x 7/9 cups.
Hence, the number of lettuce cups more than the cucumber cups is 1 x 7/9 cups.
Solve. Write your answers in simplest form.
Question 15.
Write \(\frac{4}{9}\) as a sum of fractions.
Answer:
Given that the fraction is 4/9.
The sum of the fraction of 4/9 is 1/9 + 1/9 + 1/9 + 1/9.
Question 16.
Write 1\(\frac{3}{5}\) as a sum of fractions.
Answer:
Given that the mixed fraction is 1 x (3/5)
1 x (3/5) = 8/5
The sum of the fractions of 8/5 is 1/5 + 1/5 + 1/5 + 1/5 + 1/5 + 1/5 + 1/5 +1/5.
Multiply. Write your answers in simplest form. Draw pictures if you need help.
Question 17.
4 × \(\frac{1}{3}\) = ______________
Answer:
Multiply 4 x 1/3 then you get 4/3
Question 18.
5 × \(\frac{3}{4}\) = ______________
Answer:
Multiply 5 x 3/4 then you get 23/4
Question 19.
3 × \(\frac{3}{5}\) = ______________
Answer:
Multiply 3 x 3/5 then you get 18/5
Question 20.
7 × \(\frac{4}{8}\) = ______________
Answer:
Multiply 7 x 4/8 then you get 60/8.
Solve. Write your answers in simplest form.
Question 21.
Jason is practicing for a footrace. He runs 7\(\frac{3}{8}\) miles the first week and 9\(\frac{6}{8}\) miles the second week. How many miles does Jason run in all?
Answer:
Given that,
Jason runs in the first week = 7 x (3/8) = 59/8
Jason runs in the second week = 9 x (6/8) = 78/8
The Denominators of the given fractions are same so add the numerators.
59/8 + 78/8
= 59+78/8
= 137/8
= 17 x 1/8
Hence, Jason run in all is 17 x 1/8 miles.
Question 22.
76 vehicles are in a parking lot. \(\frac{1}{4}\) of them are trucks. How many trucks are in the parking lot?
Answer:
Given that,
The total number of vehicles in the parking is 76.
The number of trucks in the parking lot is \(\frac{1}{4}\) = 1/4
Therefore 76 x 1/4 = 19.
The total number of trucks in the parking lot is 19.
Question 23.
A hardware store sold 7\(\frac{8}{10}\) feet of chain in one week. The store sold 4\(\frac{3}{10}\) feet of chain the next week. How many more feet of chain did the store sell in the first week?
Answer:
Given that,
The hardware store sold a chain in one week = 7 x (8/10) = 78/10.
The hardware store sold a chain in next week = 4 x (3/10) = 43/10.
The Denominators of the given fractions are same so subtract the numerators.
78/10 – 43/10
= 78-43/10
= 35/10
= 7/2
= 3 x 1/2
Hence, the chain sold in one week is 2 x (1/2) feet’s longer then chain sold in next week.
Question 24.
Linda travels to visit friends. She drives for a total of 23 miles. Damon also visits friends, but his trip is \(\frac{2}{3}\) as long as Linda’s. How many miles does Damon drive?
Answer:
Given that,
Linda travels to visit friends and she drives for a total of 23 miles.
Damon also visits friends, but his trip is \(\frac{2}{3}\) as long as Linda’s.
\(\frac{2}{3}\) = 2/3
Therefore Lind’s drive = 23 + 2/3 = 23 x 2/3.