Practice the questions of McGraw Hill Math Grade 4 Answer Key PDF Chapter 10 Test to secure good marks & knowledge in the exams.
McGraw-Hill Math Grade 4 Chapter 10 Test Answer Key
Place a check mark next to the best answer.
Question 1.
About how long is a paperclip?
![]()
___________ about 1 inch
___________ about 1 foot
___________ about 1 yard
Answer:

Explanation:
The paperclip is about 1 inch long.
Question 2.
About how long is a horse?

___________ about 2 centimeters
___________ about 2 kilometers
___________ about 2 meters
Answer:

Explanation:
The horse is about 2 meters long.
Multiply to find each missing number.
Question 3.
3 yd = ___________ ft
Answer:
3 yd = 9 feet
Explanation:
1 yard = 3 feet
3 yards = 3 x 3 = 9 ft
So, 3 yd = 9 ft.
Question 4.
5 mi = ___________ yd
Answer:
5 mi = 8800 yd
Explanation:
1 mile = 1760 yd
5 miles = 5 x 1760 = 8800 yd
So, 5 miles = 8800 yards.
Question 5.
4 yd = ___________ in
Answer:
4 yd = 144 in
Explanation:
1 yard = 36 inches
4 yards = 4 x 36 = 144 in
So,4 yd = 144 in.
Question 6.
13 m = ___________ cm
Answer:
13 m = 1300 cm
Explanation:
1 m = 100 cm
13 m = 13 x 100 cm
1300 cm
So, 13 cm = 1300 cm
Question 7.
48 km = ___________ m
Answer:
48 km = 48000 m
Explanation:
1 km = 1000 m
48 km = 48 x 1000 m
= 48000 m
So, 48 km = 48000 m.
Question 8.
3 mi = ___________ ft
Answer:
3 mi = 15,480 ft
Explanation:
1 mi = 5,280 ft
3 mi = 3 x 5280 ft
= 15,480 ft
So, 3 mi = 15,480 ft.
Question 9.
11 yd = ___________ in
Answer:
11 yd = 396 in
Explanation:
1 yard = 36 inches
11 yards = 11 x 36 = in
So,11 yd = 396 in.
Question 10.
17 m = ___________ cm
Answer:
17m = 1700 cm
Explanation:
1 m = 100 cm
17 m = 17 x 100 cm
= 1700 cm
So, 17 m = 1700cm.
Question 11.
5 mi = ___________ ft
Answer:
5 mi = 26,400 ft
Explanation:
1 mi = 5280 ft
5 mi = 5 x 5280 ft
26,400
So, 5 mi = 26,400 ft.
Question 12.
Draw a table to show the following data. Then convert each length to inches. Show both lengths in the table.
Maple Tree: 32 feet
Oak Tree: 75 feet
Birch Tree: 56 feet
Pine Tree: 95 feet
Answer:
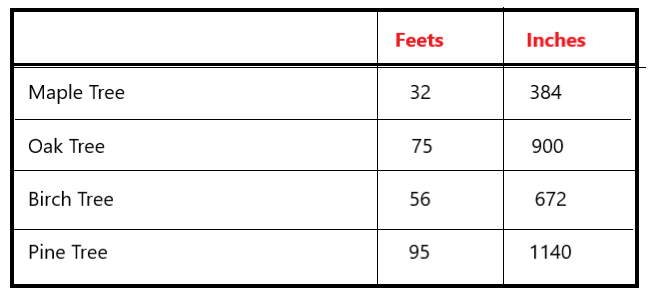
Explanation:
I drew a table to show the given data
1 feet = 12 inches
So, i converted each length from feet to inches.
Question 13.
Draw a table to show the following data. Then convert each length to centimeters. Show both lengths in the table.
Height of Garden Shed: 3 meters
Height of Garage: 4 meters
Height of House: 22 meters
Height of Mailbox: 1 meter
Answer:
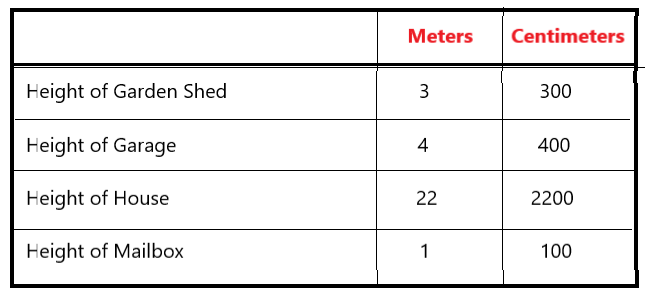
Explanation:
I drew a table to show the given data
1 meter = 100 centimeters
So, i converted each length from meters to centimeters.
Question 14.
What is the area of the rectangle?

Answer:
75 square inches
Explanation:
Area of a rectangle = length x width
Length of the given figure = 15 in
Width of the given figure = 5 in
Area – l x w = 15 x 5 = 75
So, the area of the given figure is 75 square inches.
Question 15.
What is the area of the square?

Answer:
169 square meters
Explanation:
Area of a square = length x width
Length of the given figure = 13 m
Width of the given figure = 13 m
Area – l x w = 13 x 13 = 169
So, the area of the given figure is 169 square meters.
Question 16.
What is the perimeter of the rectangle?

Answer:
54 kilometers
Explanation:
Perimeter of a rectangle = (2 x length) + (2 x width)
Length of the given figure = 18 km
Width of the given figure = 9 km
Perimeter = (2 x l) + (2 x w)
= (2 x 18) + (2 x 9)
= 36 + 18
= 54
So, perimeter of the given rectangle is 54 kilometers.
Solve.
Question 17.
Lauren and her brother went hiking. They hiked 44\(\frac{3}{8}\) kilometers along the Atlanta Trail. They also hiked 36\(\frac{2}{8}\) kilometers along the Hopper Trail. How many kilometers did they hike in all?
Answer:
80\(\frac{5}{8}\)
Explanation:
Lauren and her brother went hiking
They hiked 44\(\frac{3}{8}\) kilometers along the Atlanta Trail
They also hiked 36\(\frac{2}{8}\) kilometers along the Hopper Trail
44\(\frac{3}{8}\) + 36\(\frac{2}{8}\) = 80\(\frac{5}{8}\)
They hike 80\(\frac{5}{8}\) kilometers in all.
Question 18.
A fabric store has a sale. 22\(\frac{3}{5}\) yards of black fabric are sold the first day and 19\(\frac{1}{5}\) yards are sold the second day. 16\(\frac{1}{5}\) yards of black fabric are leftover. How many yards of black fabric were in the store to begin with?
Answer:
58 yards
Explanation:
A fabric store has a sale
22\(\frac{3}{5}\) yards of black fabric are sold the first day
19\(\frac{1}{5}\) yards are sold the second day
16\(\frac{1}{5}\) yards of black fabric are leftover
Add to find the total
22\(\frac{3}{5}\) + 19\(\frac{1}{5}\) + 16\(\frac{1}{5}\) = 58 yards
So, 58 yards of black fabric were in the store to begin.
Question 19.
Mr. Harrison is an architect. He designs a rectangular living room that is 8 meters wide and 11 meters long. What is the area of the living room?
Answer:
88 square meters
Explanation:
Mr. Harrison is an architect
He designs a rectangular living room that is 8 meters wide and 11 meters long
Area of a rectangle = length x width
Length of the living room = 11 meters
Width of the living room = 8 meters
Area – l x w = 11 x 8 = 88
So, the area of the living room is 8 square meters
Question 20.
What is the perimeter of the living room?
Answer:
38 meters
Explanation:
Perimeter of a rectangle = (2 x length) + (2 x width)
Length of the living room = 11 meters
Width of the living room = 8 meters
Perimeter = (2 x l) + (2 x w)
= (2 x 11) + (2 x 8)
= 22 + 16
= 38
So, perimeter of the living room is 38 meters.
Question 21.
Karen has a new roll of tape. She uses 3\(\frac{1}{6}\) feet to tape one package. She uses 5\(\frac{2}{6}\) feet to tape another package. Then she uses 4\(\frac{1}{6}\) feet to tape a third package. She has 12\(\frac{2}{6}\) feet of tape left over. How many feet of tape did she begin with?
Answer:
25 feet
Explanation:
Karen has a new roll of tape
She uses 3\(\frac{1}{6}\) feet to tape one package
She uses 5\(\frac{2}{6}\) feet to tape another package
Then she uses 4\(\frac{1}{6}\) feet to tape a third package
She has 12\(\frac{2}{6}\) feet of tape left over
Add to find the total
3\(\frac{1}{6}\) + 5\(\frac{2}{6}\) + 4\(\frac{1}{6}\) + 12\(\frac{2}{6}\) = 25 feet
So, Karen has 25 feet of tape with her at the beginning.