Go Math Grade 7 Answer Key Chapter 13 Theoretical Probability and Simulations: Students of 7th standard can Download the Answer Key of Go Math Chapter 13 from here. The Go Math Grade 7 Answer Key Chapter 13 Theoretical Probability and Simulations consists of the concepts like experimental and theoretical probability. We have provided a brief explanation for each and every problem to improve your math skills.
Go Math Grade 7 Answer Key Chapter 13 Theoretical Probability and Simulations
Theoretical Probability is the most interesting chapter in mathematics. Probability tells us how likely something is to happen in the long run. We can calculate the probability by looking at the outcomes of an experiment or by reasoning about the possible outcomes. If you understand the concepts of probability this is the scoring topic in the exams.
Tap on the below Go Math Grade 7 Answer Key Chapter 13 Theoretical Probability and Simulations link which is given topic-wise to get the solution with an explanation. Students can gradually improve their conceptual understanding of Math by following the HMH Go Math Grade 7 Chapter 13 Theoretical Probability and Simulations Answer Key pdf.
Chapter 13 Theoretical Probability and Simulations – Lesson: 1
Chapter 13 Theoretical Probability and Simulati+ons – Lesson: 2
Chapter 13 Theoretical Probability and Simulations – Lesson: 3
Chapter 13 Theoretical Probability and Simulations – Lesson: 4
Chapter 13 Theoretical Probability and Simulations – Lesson: 5
- 13.1, 13.2 Theoretical Probability of Simple and Compound Events – Page No. 423
- Selected Response – Page No. 424
Chapter 13 Theoretical Probability and Simulations – Lesson: 6
Chapter 13 Theoretical Probability and Simulations – Lesson: 7
Chapter 13 Theoretical Probability and Simulations – Lesson: 8
Guided Practice – Page No. 402
At a school fair, you have a choice of randomly picking a ball from Basket A or Basket B. Basket A has 5 green balls, 3 red balls, and 8 yellow balls. Basket B has 7 green balls, 4 red balls, and 9 yellow balls. You can win a digital book reader if you pick a red ball.
Question 1.
Complete the chart. Write each answer in simplest form.
Type below:
______________
Answer:
We complete the table:
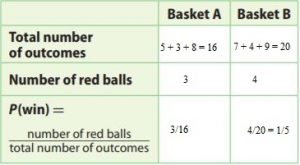
Question 2.
Which basket should you choose if you want the better chance of winning?
______
Answer: Basket B
Explanation:
In Exercise 1 we determined the probabilities Pa, Pb to pick a red ball from basket A, B
Pa = \(\frac{3}{16}\)
Pb = \(\frac{1}{5}\)
We compare the two probabilities
Pa = \(\frac{3}{16}\) . \(\frac{5}{5}\) = \(\frac{15}{80}\)
Pb = \(\frac{1}{5}\) . \(\frac{5}{5}\) = \(\frac{16}{80}\)
\(\frac{16}{80}\) > \(\frac{15}{80}\)
Pb > Pa
Since Pb > Pa, the better chance to win is in choosing Basket B.
A spinner has 11 equal-sized sections marked 1 through 11. Find each probability.
Question 3.
You spin once and land on an odd number.
\(\frac{□}{□}\)
Answer: \(\frac{6}{11}\)
Explanation:
We are given an 11 equal sized sections marked 1-11:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11
We compute the probability that spinning once we would land on an odd number (1, 3, 5, 7, 9, 11):
P(odd) = number of odd sections/total number of sections = \(\frac{6}{11}\)
Question 4.
You spin once and land on an even number.
\(\frac{□}{□}\)
Answer: \(\frac{5}{11}\)
Explanation:
We are given an 11 equal sized sections marked 1-11:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11
P(even) = number of even sections/total number of sections = \(\frac{5}{11}\)
We compute the probability that spinning once we would land on an even number (2, 4, 6, 8, 10)
You roll a number cube once.
Question 5.
What is the theoretical probability that you roll a 3 or 4?
\(\frac{□}{□}\)
Answer: \(\frac{1}{3}\)
Explanation:
P(3 or 4) = number of 3 or 4/total number of numbers on the number cube
\(\frac{2}{6}\) = \(\frac{1}{3}\)
Question 6.
Suppose you rolled the number cube 199 more times. Would you expect the experimental probability of rolling a 3 or 4 to be the same as your answer to Exercise 5?
Type below:
______________
Answer:
When rolling a number cube a large number of times, we expect the experimental probability not to be the same, but to get closer and closer to the theoretical probability.
Since 199 is not such a big number, we should not expect the experimental probability to be extremely close \(\frac{1}{3}\), but close enough.
Essential Question Check-In
Question 7.
How can you find the probability of a simple event if the total number of equally likely outcomes is 20?
Type below:
______________
Answer:
P(Simple event) = 1/total number of equally likely events
= \(\frac{1}{20}\)
Independent Practice – Page No. 403
Find the probability of each event. Write each answer as a fraction in simplest form, as a decimal to the nearest hundredth, and as a percent to the nearest whole number.
Question 8.
You spin the spinner shown. The spinner lands on yellow.
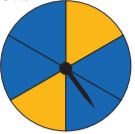
Type below:
______________
Answer: \(\frac{2}{6}\)
Explanation:
There are 2 yellow and 4 blue and we landed on yellow what is the probability of landing on yellow.
The probability is \(\frac{2}{6}\) because there are 2 yellow and the rest is blue.
Question 9.
You spin the spinner shown. The spinner lands on blue or green.
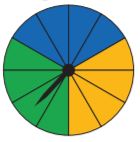
Type below:
______________
Answer: 67%
Explanation:
The yellow area, the blue area, and the green area have 3 sections each from the whole area.
We determine the probability that the spinner lands on a blue or green sections:
P(spinner lands on blue or green) = (the number of blue sections + the number of green sections)/the total number f sections
= (4 + 4)/12 = \(\frac{8}{12}\) = \(\frac{2}{3}\)
\(\frac{2}{3}\) ≈ 0.67 = 67%
Question 10.
A jar contains 4 cherry cough drops and 10 honey cough drops. You choose one cough drop without looking. The cough drop is cherry.
Type below:
______________
Answer: 28%
Explanation:
We are given the data:
A jar contains 4 cherry cough drops and 10 honey cough drops.
P(to pick a cherry drop) = (the number of cherry drops)/the total number of drops
4/(4 + 10) = \(\frac{4}{14}\) = \(\frac{2}{7}\)
\(\frac{2}{3}\) ≈ 0.28 = 28%
Question 11.
You pick one card at random from a standard deck of 52 playing cards. You pick a black card.
Type below:
______________
Answer: 50%
Explanation:
We are given the data
You pick one card at random from a standard deck of 52 playing cards.
26 red cards
26 black cards
P(to pick a black card) = the number of black cards/the total number of cards
Question 12.
There are 12 pieces of fruit in a bowl. Five are lemons and the rest are limes. You choose a piece of fruit without looking. The piece of fruit is a lime.
Type below:
______________
Answer: 58%
Explanation:
There are 12 pieces of fruit in a bowl. Five are lemons and the rest are limes.
12 fruits:
5 lemons
7 limes
P(to pick a lime) =the number of lines/the total number of fruits
W determine the probability that we pick a lime:
\(\frac{7}{12}\) ≈ 0.58 = 58%
Question 13.
You choose a movie CD at random from a case containing 8 comedy CDs, 5 science fiction CDs, and 7 adventure CDs. The CD is not a comedy.
Type below:
______________
Answer: 60%
Explanation:
We are given the data:
8 comedy CDs
5 science fiction CDs
7 adventure CDs
P(to pick a CD which is not a comedy) = (the number of Sf CDs + the number of adventure CDs)/ the total number of CDs
= (5 + 7)/(8 + 5 + 7) = \(\frac{12}{20}\) = \(\frac{3}{5}\) = 0.60 = 60%
Question 14.
You roll a number cube. You roll a number that is greater than 2 and less than 5.
Type below:
______________
Answer: 33%
Explanation:
Rolling a number greater than 2 and less than 5 means to roll one of the numbers:
3, 4
P(to roll 3 or 4) = the number of 3 or 4 numbers/the total number of numbers
= (1 + 1)/6 = \(\frac{2}{6}\) = \(\frac{1}{3}\) = 0.33 = 33%
Question 15.
Communicate Mathematical Ideas
The theoretical probability of a given event is \(\frac{9}{13}\). Explain what each number represents.
Type below:
______________
Answer:
The theoretical probability is the ratio between the number of favorable outcomes and the number of possible outcomes. The numerator 9 describes the number of desired events, while the denominator 13 describes the total number of events.
\(\frac{9}{13}\)
Question 16.
Leona has 4 nickels, 6 pennies, 4 dimes, and 2 quarters in a change purse. Leona lets her little sister Daisy pick a coin at random. If Daisy is equally likely to pick each type of coin, what is the probability that her coin is worth more than five cents? Explain.
\(\frac{□}{□}\)
Answer: \(\frac{3}{8}\)
Explanation:
Leona has 4 nickels, 6 pennies, 4 dimes, and 2 quarters in a change purse. Leona lets her little sister Daisy pick a coin at random.
1 penny = 1 cent
1 nickel = 5 cents
1 dime = 10 cents
1 quarter = 25 cents
We determine the probability that she picks a coin which is worth more than 5 cents is:
P(to pick a coin worth more than 5 cents) = the number of dimes+the number of quarters/the total number of coins
= (4 + 2)/(4 + 6 + 4 + 2) = \(\frac{6}{16}\) = \(\frac{3}{8}\) = 0.375 = 37.5%
H.O.T. – Page No. 404
Focus on Higher Order Thinking
Question 17.
Critique Reasoning
A bowl of flower seeds contains 5 petunia seeds and 15 begonia seeds. Riley calculated the probability that a randomly selected seed is a petunia seed as \(\frac{1}{3}\). Describe and correct Riley’s error.
Type below:
______________
Answer:
We are given the data
5 petunia seeds
15 begonia seeds
P(to pick a petunia seed) = the number of petunia seeds/the total number of seeds
We determine the probability that a randomly selected seed is the petunia seed
5/(5 + 15) = 5/20 = 1/4
Wrong:
Riley made the mistake in dividing the number of petunia seeds by the number of begonia seeds instead of dividing the number of petunia seeds to the total number of seeds:
P(to pick a petunia seed) = the number of petunia seeds/the total number of begonia seeds
= 5/15 = 1/3
Question 18.
There are 20 seventh graders and 15 eighth graders in a club. A club president will be chosen at random.
a. Analyze Relationships
Compare the probabilities of choosing a seventh grader or an eighth grader.
Type below:
______________
Answer:
We are given the data:
20 seventh graders
15 eighth graders
P(to pick a seventh-grader) = the number of seventh-graders/the total number of members
= 20/(20 + 15) = 20/35 = 4/7
We determine the probability of choosing a seventh-grader:
P(to pick an eighth-grader) = the number of eighth-graders/the total number of members
= 15/(20 + 15) = 15/35 = 3/7
Since 4/7 > 3/7, the probability of choosing a seventh-grader is higher than the probability of choosing an eighth-grader.
Question 18.
b. Critical Thinking
If a student from one grade is more likely to be chosen than a student from the other, is the method unfair? Explain.
Type below:
______________
Answer:
The method is not unfair because the number of seventh graders is greater than the number of eighth members (20 > 15), thus the seventh graders should be represented at a higher degree than the eighth graders.
A jar contains 8 red marbles, 10 blue ones, and 2 yellow ones. One marble is chosen at random. The color is recorded in the table, and then it is returned to the jar. This is repeated 40 times.
Question 19.
Communicate Mathematical Ideas
Use proportional reasoning to explain how you know that for each color, the theoretical and experimental probabilities are not the same.
Type below:
______________
Answer:
We are given the data
8 red marbles
10 blue marbles
2 yellow marbles
We determine the theoretical probability Pt of choosing each type of marble:
Pt(to pick a red marble) = the number of red marbles/the total number of marbles
= 8/(8 + 10 + 2) = 8/20 = 4/10
Pt(to pick a blue marble) = the number of blue marbles/the total number of marbles
= 10/(8 + 10 + 2) = 10/20 = 5/10
Pt(to pick a yellow marble) = the number of yellow marbles/the total number of marbles
= 2/(8 + 10 + 2) = 2/20 = 1/10
We determine the theoretical probability Pe of choosing each type of marble
Pe(to pick a red marble) = the number of red marbles/the total number of marbles
14/14+16+10 = 14/40 = 7/20
Pe(to pick a blue marble) = the number of blue marbles/the total number of marbles
16/14+16+10 = 16/40 = 8/20
Pe(to pick a yellow marble) = the number of yellow marbles/the total number of marbles
10/14+16+10 = 10/40 = 5/20
We notice that the number of red marbles is 4 times the number of yellow marbles, thus the theoretical probability to choose a red marble is 4 times greater than the one of choosing a yellow marble, while the experimental case shows that the probability of choosing a red marble is less than 1.5 times greater than the one of choosing a yellow one.
In the same way, we notice that the number of blue marbles is 5 times the number of yellow marbles, thus the theoretical probability to choose a blue marble is 5 times greater than the one of choosing a yellow marble, while the experimental case shows that the probability of choosing a blue marble is less than 2 times greater than the one of choosing a yellow one.
The exact probabilities are computed above.
Question 20.
Persevere in Problem Solving
For which color marble is the experimental probability closest to the theoretical probability? Explain.
______________
Answer:
We are given the data
8 red marbles
10 blue marbles
2 yellow marbles
Pt(to pick a red marble) = 8/20 = 4/10
Pt(to pick a blue marble) = 10/20 = 5/10
Pt(to pick a yellow marble) = 2/20 = 1/10
Pe(to pick a red marble) = 14/40 = 7/20
Pe(to pick a blue marble) = 16/40 = 8/20
Pe(to pick a yellow marble) = 10/40 = 5/20
|\(\frac{7}{20}\) – \(\frac{8}{20}\)| = \(\frac{1}{20}\)
|\(\frac{8}{20}\) – \(\frac{10}{20}\)| = \(\frac{2}{20}\)
|\(\frac{5}{20}\) – \(\frac{2}{20}\)| = \(\frac{3}{20}\)
\(\frac{1}{20}\) < \(\frac{2}{20}\) < \(\frac{3}{20}\)
Thus the answer is red.
Guided Practice – Page No. 408
Drake rolls two fair number cubes.
Question 1.
Complete the table to find the sample space for rolling a particular product on two number cubes.
Type below:
______________
Answer:
We complete the table to find the sample space for rolling a particular product on two number cubes:
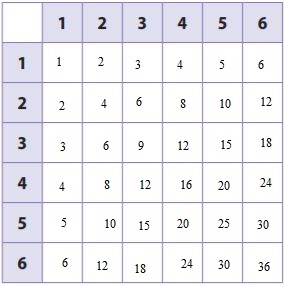
Question 2.
What is the probability that the product of the two numbers Drake rolls is a multiple of 4?
\(\frac{□}{□}\)
Answer: \(\frac{5}{12}\)
Explanation:

We find the products which are multiplies of 4:
4, 4, 8, 12, 12, 4, 8, 12, 14, 20, 24, 20, 12, 24, 36.
The number of multiples of 4 is 15.
The total number of products is
6 × 6 = 36
We determine the probability that the product is multiple of 4:
\(\frac{15}{36}\) = \(\frac{5}{12}\)
Question 3.
What is the probability that the product of the two numbers Drake rolls is less than 13?
\(\frac{□}{□}\)
Answer: \(\frac{23}{36}\)
Explanation:

We find products which are less than 13:
1, 2, 3, 4, 5, 6, 2, 4, 6, 8, 10, 12, 3, 6, 9, 12, 4, 8, 12, 5, 10, 6, 12
The number of products of less than 13 is 6 × 6 = 36.
The total number of products is
23/36
You flip three coins and want to explore probabilities of certain events.
Question 4.
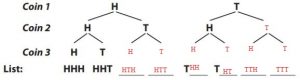
Complete the tree diagram and make a list to find the sample space.
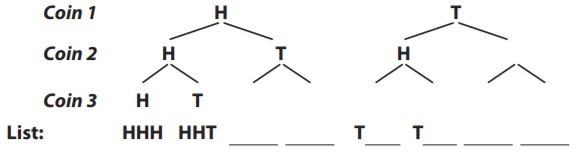
Type below:
______________
Answer:
We complete the given tree diagram placing one H and one T under each H and each T:
Question 5.
How many outcomes are in the sample space?
_______
Answer: 8 outcomes
Explanation:

Since each coin can land in two possible ways, the total possible number of outcomes is
2³ = 8
Thus there are 8 outcomes in the sample space.
Question 6.
List all the ways to get three tails.
Type below:
______________
Answer:
We are given the tree diagram we determined in Exercise 4:

The list of the 8 possible outcoes is
HHH, HHT, HTH, HTT, THH, THT, TTH, TTT
We list the outcomes containing 3 tails is TTT.
Question 7.
Complete the expression to find the probability of getting three tails.
\(\frac{□}{□}\)
Answer: \(\frac{1}{8}\)
Explanation:
P = number of outcomes with 3T/ total number of possible outcomes
The probability of getting three tails when three coins are flipped is \(\frac{1}{8}\)
Question 8.
What is the probability of getting exactly two heads?
\(\frac{□}{□}\)
Answer: \(\frac{3}{8}\)
Explanation:
The list of the 8 possible outcomes is:
HHH, HHT, HTH, HTT, THH, THT, TTH, TTT
We list the outcomes of 2H
HHT, HTH, THH
There are 3 ways to obtain exactly two heads is HHT, HTH, THH
P = number of outcomes with 3H/ total number of possible outcomes
P = \(\frac{3}{8}\)
Essential Question Check-In
Question 9.
There are 6 ways a given compound event can occur. What else do you need to know to find the theoretical probability of the event?
Type below:
______________
Answer:
We know that there are 6 ways in which a given compound event can occur and thus there are 6 favorable outcomes.
favorable outcomes = 6
The probability is the number of favorable outcomes divided by the number of possible outcomes
P(event) = favorable outcomes/possible outcomes
Since we know the number of favorable outcomes, we also require the number of possible outcomes in order to determine the probability.
Independent Practice – Page No. 409
In Exercises 10–12, use the following information. Mattias gets dressed in the dark one morning and chooses his clothes at random. He chooses a shirt (green, red, or yellow), a pair of pants (black or blue), and a pair of shoes (checkered or red).
Question 10.
Use the space below to make a tree diagram to find the sample space.
Type below:
______________
Answer:
The sample space is:
Green Blue Red
Green Blue Checkered
Green Black Red
Green Black Checkered
Red Blue Red
Red Blue Checkered
Red Black Red
Red Black Checkered
Yellow Blue Red
Yellow Blue Checkered
yellow Black Red
Yellow Black Checkered
Question 11.
What is the probability that Mattias picks an outfit at random that includes red shoes?
\(\frac{□}{□}\)
Answer: \(\frac{1}{2}\)
Explanation:
Shirt Pants Shoes:
Green Blue Red
Green Blue Checkered
Green Black Red
Green Black Checkered
Red Blue Red
Red Blue Checkered
Red Black Red
Red Black Checkered
Yellow Blue Red
Yellow Blue Checkered
Yellow Black Red
Yellow Black Checkered
P = the number of outfits with red shoes/the total number of outfits
P = \(\frac{6}{12}\)
P = \(\frac{1}{2}\)
Question 12.
What is the probability that no part of Mattias’s outfit is red?
\(\frac{□}{□}\)
Answer: \(\frac{1}{3}\)
Explanation:
Shirt Pants Shoes:
Green Blue Red
Green Blue Checkered
Green Black Red
Green Black Checkered
Red Blue Red
Red Blue Checkered
Red Black Red
Red Black Checkered
Yellow Blue Red
Yellow Blue Checkered
Yellow Black Red
Yellow Black Checkered
P = the number of outfits with no red shoes/the total number of outfits
P = \(\frac{4}{12}\)
P = \(\frac{1}{3}\)
Question 13.
Rhee and Pamela are two of the five members of a band. Every week, the band picks two members at random to play on their own for five minutes. What is the probability that Rhee and Pamela are chosen this week?
\(\frac{□}{□}\)
Answer: \(\frac{1}{10}\)
Explanation:
Let’s note the 5 members of the band:
R = Rhee
P = Pamela
A, B, C = the other 3 members
The list of the possible outcomes is:
RP, RA, RB, RC, PR, PA, PB, AP, AR, AB, AC, BP, BR, BA, BC, CP, CR, CA, CB.
P = the number of outcomes containing P and R/the total number of outcomes
P = \(\frac{2}{20}\)
P = \(\frac{1}{10}\)
Question 14.
Ben rolls two number cubes. What is the probability that the sum of the numbers he rolls is less than 6?
\(\frac{□}{□}\)
Answer: \(\frac{5}{18}\)
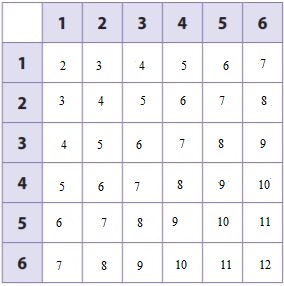
The sums less than 6 are:
2, 3, 4, 5, 3, 4, 5, 4, 5, 5
P = the number of sums less than 6/the total number of sums
P = \(\frac{10}{36}\)
P = \(\frac{5}{18}\)
Question 15.
Nhan is getting dressed. He considers two different shirts, three pairs of pants, and three pairs of shoes. He chooses one of each of the articles at random. What is the probability that he will wear his jeans but not his sneakers?
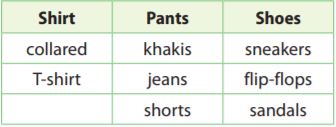
\(\frac{□}{□}\)
Answer: \(\frac{2}{9}\)
Explanation:
We are given the data
Shirt: collared/T-shirt
Pants: Khakis/jeans/shorts
Shoes: sneakers/flip-flops/sandals
We determine the outcomes including jeans and not sneakers
P = the outcome including jeans and not sneakers/all possible outcomes
P = \(\frac{4}{18}\) = \(\frac{2}{9}\)
Question 16.
Communicate Mathematical Ideas
A ski resort has 3 chair lifts, each with access to 6 ski trails. Explain how you can find the number of possible outcomes when choosing a chair lift and a ski trail without making a list, a tree diagram, or table.
Type below:
______________
Answer: 18
Explanation:
We are given the data:
Chair lifts: Chair lift 1/chair lift 2/chair lift 3
Ski trails: ski trail 1/ski trail 2/ski trail 3/ski trail 4/ski trail 5/ski trail 6
The sample space for choosing one of each is the product between the number of chair lifts and the number of ski lifts:
3 × 6 = 18
Question 17.
Explain the Error
For breakfast, Sarah can choose eggs, granola or oatmeal as a main course, and orange juice or milk for a drink. Sarah says that the sample space for choosing one of each contains 32 = 9 outcomes. What is her error? Explain.
Type below:
______________
Answer:
We are given the data:
Main course: eggs/granola/oatmeal
Drink: orange juice/milk
The sample space for choosing one of each is:
3 × 2 = 6
eggs-orange juice
eggs-milk
granola-orange juice
granola-milk
oatmeal-orange juice
oatmeal-milk
The error made by Sarah is that she considered only the number of main courses and forgetting the number of drinks.
Page No. 410
Question 18.
Represent Real-World Problems
A new shoe comes in two colors, black or red, and in sizes from 5 to 12, including half sizes. If a pair of the shoes is chosen at random for a store display, what is the probability it will be red and size 9 or larger?
\(\frac{□}{□}\)
Answer: \(\frac{7}{30}\)
Explanation:
We are given the data
Colors: black/red
Sizes: 5/5.5/6/6.5/7/7.5/8/8.5/9/9.5/10/10.5/11/11.5/12
The possible outcomes of red shoes with size greater or equal 9 are
red 9
red 9.5
red 10
red 10.5
red 11
red 11.5
red 12
P = the number of red shoes with size greater or equal 9/the total number of outcomes
P = 7/(2 × 15) = \(\frac{7}{30}\)
H.O.T.
Focus on Higher Order Thinking
Question 19.
Analyze Relationships
At a diner, Sondra tells the server, “Give me one item from each column.” Gretchen says, “Give me one main dish and a vegetable.” Who has a greater probability of getting a meal that includes salmon? Explain.
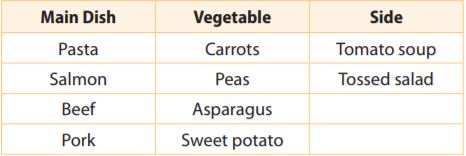
______________
Answer:
We are given the data:
Main Dish: Pasta/salmon/beef/pork
Vegetable: carrots/peas/asparagus/sweet potato
Side: tomato soup/tossed salad
Psondra = (1 . 4 . 2)/(4 . 4 . 2) = \(\frac{8}{32}\) = \(\frac{1}{4}\)
Pgretchen = 4/16 = \(\frac{1}{4}\)
Question 20.
The digits 1 through 5 are used for a set of locker codes.
a. Look for a Pattern
Suppose the digits cannot repeat. Find the number of possible two-digit codes and three-digit codes. Describe any pattern and use it to predict the number of possible five-digit codes.
Type below:
______________
Answer: 20, 60, 120
Explanation:
We are given the data
Digits: 1, 2, 3, 4, 5
We find the two digits codes when digits do not repeat
12, 13, 14, 15
21, 23, 24, 25
31, 32, 34, 35
41, 42, 43, 45
51, 52, 53, 54
There are 5 × 4 = 20 possible codes.
We find the three digits codes when digits do not repeat:
123, 124, 125
132, 134, 135
142, 143, 145
152, 153, 154
213, 214, 215
231, 124, 135
…
….
512, 513, 514
521, 523, 524
531, 532, 534
541, 542, 543
There are 5 × 4 × 3 = 60 possible outcomes
If we use 5 digits and none can repeat, the first digit can be one of the numbers 1 2 3 4 5, the second digit can be one of the 4 remaining numbers, the third digit is one of the 3 remaining numbers, the fourth digit is one of the two remaining numbers, thus the number of possible outcomes is:
5 × 4 × 3 × 2 = 120
Question 20.
b. Look for a Pattern
Repeat part a, but allow digits to repeat.
Type below:
______________
Answer:
We find the two digits codes when digits can repeat:
11, 12, 13, 14, 15,
21, 22, 23, 24, 25
31, 32, 33, 34, 35
41, 42, 43, 44, 45
51, 52, 53, 54, 55
There are 5 . 5 = 25 possible codes.
There are 5 × 5 × 5 = 125 possible codes.
If we use 5 digits and they can repeat, the first digit can be one of the numbers 1 2 3 4 5, the second digit can be one of the same numbers 1 2 3 4 5, the third digit is one of the 5 numbers, the fourth digit is one of the 5 numbers, the fifth digit is one of the 5 numbers, thus the number of possible outcomes is
5 × 5 × 5 × 5 × 5 = 3125
Question 20.
c. Justify Reasoning
Suppose that a gym plans to issue numbered locker codes by choosing the digits at random. Should the gym use codes in which the digits can repeat or not? Justify your reasoning.
Type below:
______________
Answer:
The probability P1 to get a 2 digits code when digits do not repeat and the probability P2 to get a 2 digits code when digits can repeat:
P1 = 1/20
P2 = 1/25
The probability P1 to get a 3 digits code when digits do not repeat and the probability P2 to get a 3 digits code when digits can repeat:
P1 = 1/60
P2 = 1/125
The probability P1 to get a 5 digits code when digits do not repeat and the probability P2 to get a 5 digits code when digits can repeat:
P1 = 1/120
P2 = 1/3125
Thus the gym should use codes in which digits can repeat because the probability to be guessed is much smaller.
Guided Practice – Page No. 414
Question 1.
Bob works at a construction company. He has an equally likely chance to be assigned to work different crews every day. He can be assigned to work on crews building apartments, condominiums, or houses. If he works 18 days a month, about how many times should he expect to be assigned to the house crew?
_______ times
Answer:
Step 1:
Apartment: \(\frac{1}{3}\) Condo: \(\frac{1}{3}\) House: \(\frac{1}{3}\)
Probability of being assigned to the house crew: \(\frac{1}{3}\)
Step 2:
\(\frac{1}{3}\) = \(\frac{x}{18}\)
x = 6
6 times out of 18.
Question 2.
During a raffle drawing, half of the ticket holders will receive a prize. The winners are equally likely to win one of three prizes: a book, a gift certificate to a restaurant, or a movie ticket. If there are 300 ticket holders, predict the number of people who will win a movie ticket.
_______ people
Answer: 50 people
Explanation:
If 300 people buy tickets and half of them will receive a prize then 300 × 1/2 = 150 ticket holders will receive a prize. If they are equally likely to win one of the three prizes, then the probability of winning a movie ticket is 1/3. The number of people who will win a movie ticket is then 1/3 × 150 = 50 people.
Question 3.
In Mr. Jawarani’s first period math class, there are 9 students with hazel eyes, 10 students with brown eyes, 7 students with blue eyes, and 2 students with green eyes. Mr. Jawarani picks a student at random. Which color eyes is the student most likely to have? Explain.
______________
Answer: Brown
Explanation:
There are more students with brown eyes then any other colored eyes so if he picks a student at random, they will most likely have brown eyes.
Essential Question Check-In
Question 4.
How do you make predictions using theoretical probability?
Type below:
______________
Answer:
To make a prediction using theoretical probability, you can multiply the theoretical probability by the number of events to get a prediction. You can find the prediction by setting the theoretical probability equal to the ratio of x/number of events and then solving for x, where x is the prediction.
Independent Practice – Page No. 415
Question 5.
A bag contains 6 red marbles, 2 white marbles, and 1 gray marble. You randomly pick out a marble, record its color, and put it back in the bag. You repeat this process 45 times. How many white or gray marbles do you expect to get?
_______ marbles
Answer: 15
Explanation:
Given that there are 6 red marbles, 2 white marbles, and 1 gray marble, which are thus 6 + 2 + 1 = 9 marbles in total.
possible outcomes = 9
2 + 1 = 3 of the marbles are either white or gray and thus there are 3 favorable outcomes.
favorable outcomes = 3
The probability is the number of favorable outcomes divided by the number of possible outcomes.
P(white or gray) = favorable outcomes/possible outcomes = \(\frac{3}{9}\)
= \(\frac{1}{3}\)
The predicted number of white or gray marbles is then obtained by multiplying the number of repetitions by the probability.
Prediction = Number of repetitions × P (white or gray)
= 45 × \(\frac{1}{3}\)
= 15
Thus we predict that we obtain a white or gray marble about 15 times.
Question 6.
Using the blank circle below, draw a spinner with 8 equal sections and 3 colors—red, green, and yellow. The spinner should be such that you are equally likely to land on green or yellow, but more likely to land on red than either on green or yellow.

Type below:
______________
Answer:
A possible spinner would be to have 4 red sections, 2 green sections, and 2 yellow sections. That way there is an equal chance of landing on yellow and green and there is a more likely chance of landing on yellow and green and there is a more likely chance of landing on red than landing on green or landing on yellow.
A second possible spinner could be to have 6 red sections, 1 yellow section, and 1 green section. This would still give an equal chance to land on green or yellow and a higher chance to land on red than to land on green or land on yellow.
Use the following for Exercises 7–9. In a standard 52-card deck, half of the cards are red and half are black. The 52 cards are divided evenly into 4 suits: spades, hearts, diamonds, and clubs. Each suit has three face cards (jack, queen, king), and an ace. Each suit also has 9 cards numbered from 2 to 10.
Question 7.
Dawn draws 1 card, replaces it, and draws another card. Is it more likely that she draws 2 red cards or 2 face cards?
______________
Answer: 2 red cards
Explanation:
There are 26 red cards in the deck and 12 face cards in the deck so it is more likely to draw two red cards than it is to draw two face cards.
Question 8.
Luis draws 1 card from a deck, 39 times. Predict how many times he draws an ace.
_______ times
Answer: About 3 times
Explanation:
A standard deck of cards contains 52 cards, of which 26 are red and 26 are black, 13 are of each suit (hearts, diamonds, spades, clubs), and of which 4 are of each denomination (A, 2 to 10, J, Q, K). The face cards are the jacks J, queens Q, and kings K.
There are 52 cards in the deck of cards and thus there 52 possible outcomes.
possible outcomes = 52
4 of the 52 cards in a standard deck of cards area aces and thus there are 4 favorable outcomes.
favorable outcomes = 4
The probability is the number of favorable outcomes divided by the number of possible outcomes.
P(white or gray) = favorable outcomes/possible outcomes = \(\frac{4}{52}\)
= \(\frac{1}{13}\)
The predicted number of aces is then obtained by multiplying the number of draws by the probability.
Prediction = Number of draws × P(Ace)
= 39 × \(\frac{1}{3}\)
Thus we predict that 3 of the drawn cards will be aces.
Question 9.
Suppose a solitaire player has played 1,000 games. Predict how many times the player turned over a red card as the first card.
_______ times
Answer: 500 times
Explanation:
A standard deck of cards contains 52 cards, of which 26 are red and 26 are black, 13 are of each suit (hearts, diamonds, spades, clubs) and of which 4 are of each denomination (A, 2 to 10, J, Q, K). The face cards are the jacks J, queens Q and kings K.
There are 52 cards in the deck of cards and thus there 52 possible outcomes.
possible outcomes = 52
26 of the 52 cards in a standard deck of cards are red. This then implies that there are 26 favorable outcomes.
favorable outcomes = 26
The probability is the number of favorable outcomes divided by the number of possible outcomes
P(red) = favorable outcomes/possible outcomes = \(\frac{26}{52}\) = 1/2
The predicted number of aces is then obtained by multiplying the number of draws by the probability.
Prediction = Number of draws × P(Red)
= 1000 × \(\frac{1}{2}\)
= 500
Thus we predict that 500 of the drawn cards will be red.
Question 10.
John and O’Neal are playing a board game in which they roll two number cubes. John needs to get a sum of 8 on the number cubes to win. O’Neal needs a sum of 11. If they take turns rolling the number cube, who is more likely to win? Explain.
______________
Answer: John
Explanation:
To get a sum of 8, John can roll the following numbers:
2, 6
3, 5
4, 4
5, 3
6, 2
To get a sum of 11, O’Neal can roll the following numbers:
5, 6
6, 5
Since there are more ways to roll a sum of 8 than there are to roll a sum of 11, John is more likely to win.
Question 11.
Every day, Navya’s teacher randomly picks a number from 1 to 20 to be the number of the day. The number of the day can be repeated. There are 180 days in the school year. Predict how many days the number of the day will be greater than 15.
_______ days
Answer: 45 days
Explanation:
There are 20 numbers from 1 to 20 and thus there are 20 possible outcomes.
possible outcomes = 20
5 of the 20 numbers from 1 to 20 are greater than 15 (16, 17, 18, 19, 20) and thus there are 5 favorable outcomes.
favorable outcomes = 5
The probability is the number of favorable outcomes divided by the number of possible outcomes
P(greater than 15) = favorable outcomes/possible outcomes = \(\frac{5}{20}\) = \(\frac{1}{4}\)
The predicted is the number of favorable outcomes divided by the number of possible outcomes/
Prediction = Number of days × P(Greater than 15)
180 × \(\frac{1}{4}\)
= 45
Thus we predict that 45 of the days have a number greater than 15.
Question 12.
Eben rolls two standard number cubes 36 times. Predict how many times he will roll a sum of 4.
_______ times
Answer: 3 times
Explanation:
A number cube has 6 possible outcomes: 1, 2, 3, 4, 5, 6.
There are then 6 × 6 = 36 possible outcomes when rolling 2 dice.
possible outcomes = 6 . 6 = 36
3 of the outcomes in the image below result in a sum of 4 ((1, 3), (2, 2), (3, 1)) and thus there are 3 favorable outcomes.
favorable outcomes = 3
The probability is the number of favorable outcomes divided by the number of possible outcomes
P(sum is 4) = favorable outcomes/possible outcomes = \(\frac{3}{36}\) = 1/12
The predicted is the number of rolls that result in a sum of 4 is then obtained by multiplying the number of rolls by the probability.
Prediction = Number of rolls × P(sum is 4)
= 36 × 1/12
= 3
Thus we predict that 3 of the rolls result in a sum of 4.
Question 13.
Communicate Mathematical Ideas
Can you always show that a prediction based on theoretical probability is true by performing the event often enough? If so, explain why. If not, describe a situation that justifies your response.
Type below:
______________
Answer:
You cannot show that a prediction based on theoretical probability is true by performing the event often enough. The prediction value will get closer to the actual value as more events are performed but will not always equal the actual value.
Page No. 416
Question 14.
Represent Real-World Problems
Give a real-world example of an experiment in which all of the outcomes are not equally likely. Can you make a prediction for this experiment, using theoretical probability?
Type below:
______________
Answer:
A real work example of an experiment in which all of the outcomes are not equally likely could be spinning a spinner that has 1 red section, 2 orange sections, and 3 blue sections, and the sections are of the same size. Since there are not the same number of sections for each other, the outcomes of red, orange, and blue do not have the same probabilities. A prediction can still be made because the theoretical probabilities of landing on each color can be found. If you wanted to predict the number of times you would land on blue in 100 spins, you would first need to find the theoretical probability of landing on blue. Since there are 3 blue sections and a total of 6 sections, the theoretical probability is \(\frac{3}{6}\) = \(\frac{1}{2}\). The prediction would then be \(\frac{1}{2}\) × 100 = 50 times.
H.O.T.
Focus on Higher Order Thinking
Question 15.
Critical Thinking
Pierre asks Sherry a question involving the theoretical probability of a compound event in which you flip a coin and draw a marble from a bag of marbles. The bag of marbles contains 3 white marbles, 8 green marbles, and 9 black marbles. Sherry’s answer, which is correct, is \(\frac{12}{40}\). What was Pierre’s question?
Type below:
______________
Answer: What is the probability of drawing a white or black marble and flipping heads?
Question 16.
Make a Prediction
Horace is going to roll a standard number cube and flip a coin. He wonders if it is more likely that he rolls a 5 and the coin lands on heads, or that he rolls a 5 or the coin lands on heads. Which event do you think is more likely to happen? Find the probability of both events to justify or reject your initial prediction.
Type below:
______________
Answer:
It is more likely that he rolls a 5 or flips heads than it is to roll a 5 and flip heads. This is because the probability of two events occurring at the same time is always less than the probability of one or another event occurring. The probability of rolling a 5 is 1/6 and the probability of flipping heads is 1/2 so the probability of both occurring is 1/6 × 1/2 = 1/12.
There are 12 possible outcomes to rolling a number cube and flipping a coin since there are 6 outcomes for the cube and 2 outcomes for the coin and 6 × 2 = 12.
Of those 12 outcomes, 7 of them are rolling a 5 or flipping heads (1H, 2H, 3H, 4H, 5H, 6H, 5T). The probability of rolling a 5 or flipping heads is then 7/12 which is greater than 1/12.
Question 17.
Communicate Mathematical Ideas
Cecil solved a theoretical prediction problem and got this answer: “The spinner will land on the red section 4.5 times.” Is it possible to have a prediction that is not a whole number? If so, give an example.
Type below:
______________
Answer: Yes
It is possible if what is being predicted does not have to be a whole number, like time. A possible example could be, the theoretical probability that there will be 50 people in a line at a store during a one-hour interval is 1/12. What is the predicted number of hours that there will be 50 people in line if the store is open for 9 hours? The prediction would then be 1/12 × 9 = 0.75 hours.
Guided Practice – Page No. 420
There is a 30% chance that T’Shana’s county will have a drought during any given year. She performs a simulation to find the experimental probability of a drought in at least 1 of the next 4 years.
Question 1.
T’Shana’s model involves the whole numbers from 1 to 10. Complete the description of her model.
Type below:
______________
Answer:
Since the chance of drought is 30%, let the numbers 1 to 3 represent a drought year and the numbers 4 to 10 represent a year without a drought. Since you are concerned with the number of droughts in the next 4 years, generate 4 random numbers in each trial.
Question 2.
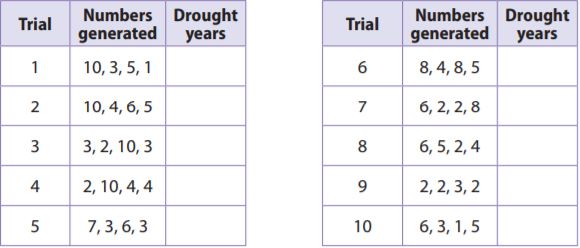
Suppose T’Shana used the model described in Exercise 1 and got the results shown in the table. Complete the table.
Type below:
______________
Answer:
The number of drought years is the number of times 1 to 3 was generated in each trial so count the number of times in each trial that the number 1 to 3 occurred:
Question 3.
According to the simulation, what is the experimental probability that there will be a drought in the county in at least 1 of the next 4 years?
\(\frac{□}{□}\)
Answer: \(\frac{4}{5}\)
Explanation:
There are 10 trials and thus there are 10 possible outcomes.
possible outcomes = 10
In the previous exercise, we obtained at least 1 drought year in 8 of the 10 trials and thus there are 8 favorable outcomes.
favorable outcomes = 8
The probability is the number of favorable outcomes divided by the number of possible outcomes.
P(At least 1 drought year) = favorable outcomes/possible outcomes = \(\frac{8}{10}\)
= \(\frac{4}{5}\) = 0.8 = 80%
Essential Question Check-In
Question 4.
You want to generate random numbers to simulate an event with a 75% chance of occurring. Describe a model you could use.
Type below:
______________
Answer:
75% in fraction form is \(\frac{3}{4}\) so you can randomly generate numbers from 1 to 4. The numbers 1 to 3 would mean success and 4 would mean unsuccessful.
Independent Practice – Page No. 421
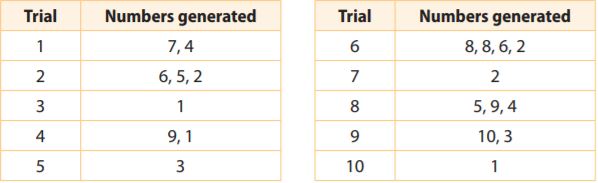
Every contestant on a game show has a 40% chance of winning. In the simulation below, the numbers 1–4 represent a winner, and the numbers 5–10 represent a nonwinner. Numbers were generated until one that represented a winner was produced.
Question 5.
In how many of the trials did it take exactly 4 contestants to get a winner?
_____ trial(s)
Answer: 1
Explanation:
Only trial 6 took 4 contestants to get a winner so 1 trial.
Question 6.
Based on the simulation, what is the experimental probability that it will take exactly 4 contestants to get a winner?
\(\frac{□}{□}\)
Answer: \(\frac{1}{10}\)
Explanation:
We have data about 10 trials and thus there are 10 possible outcomes.
possible outcomes = 10
1 of the 10 trials required exactly 4 numbers to get a winner and thus there is 1 favorable outcome.
favorable outcomes = 1
The probability is the number of favorable outcomes divided by the number of possible outcomes
P(exactly 4 contestants) = favorable outcomes/possible outcomes = \(\frac{1}{10}\) = 0.1 = 10%
Over a 100-year period, the probability that a hurricane struck Rob’s city in any given year was 20%. Rob performed a simulation to find an experimental probability that a hurricane would strike the city in at least 4 of the next 10 years. In Rob’s simulation, 1 represents a year with a hurricane.
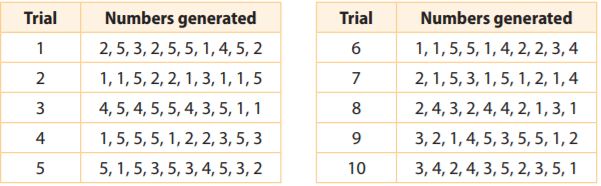
Question 7.
According to Rob’s simulation, what was the experimental probability that a hurricane would strike the city in at least 4 of the next 10 years?
\(\frac{□}{□}\)
Answer: \(\frac{1}{5}\)
Explanation:
We have been given data about 10 trials and thus there are 10 possible outcomes.
possible outcomes = 10
A 1 represents a hurricane. We then note that trial 2 and trial 7 both have at least 4 ones and thus there are 4 trials that result in at least 4 hurricanes.
Thus there are 2 favorable outcomes.
favorable outcomes = 2
The probability is the number of favorable outcomes divided by the number of possible outcomes
P(At least 4) = favorable outcomes/possible outcomes = \(\frac{2}{10}\) = \(\frac{1}{5}\)
= 0.2 = 20%
Question 8.
Analyze Relationships
Suppose that over the 10 years following Rob’s simulation, there was actually 1 year in which a hurricane struck. How did this compare to the results of Rob’s simulation?
Type below:
______________
Answer:
If a hurricane struck in 1 year the next 10 years following the simulation, it would match with the results of his simulation. In 3 of his trials, exactly 1 year had a hurricane which means the experimental probability that there will be 1 hurricane in 10 years is \(\frac{3}{10}\).
In all of the trials, there was at least 1 year with a hurricane which means the experimental probability is 100% that a hurricane will occur the next 10 years.
Page No. 422
Question 9.
Communicate Mathematical Ideas
You generate three random whole numbers from 1 to 10. Do you think that it is unlikely or even impossible that all of the numbers could be 10? Explain?
Type below:
______________
Answer:
It is unlikely that all three numbers would be 10. The theoretical probability that a random whole number from 1 to 10 is 10 is 1/10.
The theoretical probability that three random whole numbers from 1 to 10 are all 10s is then \(\frac{1}{10}\) × \(\frac{1}{10}\) × \(\frac{1}{10}\) = \(\frac{1}{1000}\).
This is a very small probability so it is unlikely.
Question 10.
Erika collects baseball cards, and 60% of the packs contain a player from her favorite team. Use a simulation to find an experimental probability that she has to buy exactly 2 packs before she gets a player from her favorite team
Type below:
______________
Answer:
Generate random numbers from 1 to 10 using 10 trials. Since 60% of the packs contain a player from her favorite team, let the numbers 1 to 6 represent a pack with a player from her favorite team and the numbers 7 to 10 represent packs without a player from her favorite team.
Out of 10 trials she had to buy exactly 10 packs before getting a player from her favorite team only in 2 trials so the experimental probability is \(\frac{2}{10}\) = \(\frac{1}{5}\).
H.O.T.
Focus on Higher Order Thinking
Question 11.
Represent Real-World Problems
When Kate plays basketball, she usually makes 37.5% of her shots. Design and conduct a simulation to find the experimental probability that she makes at least 3 of her next 10 shots. Justify the model for your simulation.
Type below:
______________
Answer: \(\frac{7}{10}\)
Explanation:
Since 37.5% = 3/8 perform simulation by randomly generating 10 members from 1 to 8 where the numbers 1 to 3 are when she makes the shot and 4 to 8 are when she doesn’t make the shot. Perform 10 trials.
She made at least 3 shots in 7 of the 10 trials so the experimental probability is \(\frac{7}{10}\)
Question 12.
Justify Reasoning
George and Susannah used a simulation to simulate the flipping of 8 coins 50 times. In all of the trials, at least 5 heads came up. What can you say about their simulation? Explain.
Type below:
______________
Answer:
If at least 5 heads came up in every trial, then the simulation they used does not accurately model flipping a coin 8 times. Since each coin has a theoretical probability of 1/2 and \(\frac{1}{2}\) × 8 = 4, there should be around 4 heads in each trial. Getting at least 5 heads in every trial means that the coin is more likely to land on heads than to land on tails.
13.1, 13.2 Theoretical Probability of Simple and Compound Events – Page No. 423
Find the probability of each event. Write your answer as a fraction, as a decimal, and as a percent.
Question 1.
You choose a marble at random from a bag containing 12 red, 12 blue, 15 green, 9 yellow, and 12 black marbles. The marble is red.
Type below:
______________
Answer:
The bag contains 12 red, 12 blue, 15 green, 9 yellow, and 12 black marbles, which are thus 12 + 12 + 15 + 9 + 12 = 60 marbles in total and thus there are 60 possible outcomes.
possible outcomes = 60
12 of the 60 marbles are red and thus there are 12 favorable outcomes.
favorable outcomes = 12
The probability is the number of favorable outcomes divided by the number of possible outcomes
P(red) = favorable outcomes/possible outcomes = \(\frac{12}{60}\) = 1/5 = 0.2 = 20%
Question 2.
You draw a card at random from a shuffled deck of 52 cards. The deck has four 13-card suits (diamonds, hearts, clubs, spades). The card is a diamond or a spade.
Type below:
______________
Answer:
A standard deck of cards contains 52 cards, of which 26 are red and 26 are black, 13 are of each suit (hearts, diamonds, spades, clubs) and of which 4 are of each denomination (A, 2 to 10, J, Q, K). The face cards are the jacks J, queens Q and kings K.
There are 52 cards in the deck of cards and thus there 52 possible outcomes.
possible outcomes = 52
13 of the cards are diamonds and 13 of the cards are spades, thus there are 13 + 13 = 26 cards that are diamonds or spades. This then implies that there are 26 favorable outcomes.
favorable outcomes = 26
The probability is the number of favorable outcomes divided by the number of possible outcomes
P(red) = favorable outcomes/possible outcomes = \(\frac{26}{52}\) = 1/2 = 50%
13.3 Making Predictions with Theoretical Probability
Question 3.
A bag contains 23 red marbles, 25 green marbles, and 18 blue marbles. You choose a marble at random from the bag. What color marble will you most likely choose?
______________
Answer: Green
Explanation:
There are more green marbles than any other color so you are more likely to choose a green marble.
13.4 Using Technology to Conduct a Simulation
Question 4.
Bay City has a 25% chance of having a flood in any given decade. The table shows the results of a simulation using random numbers to find the experimental probability that there will be a flood in Bay City in at least 1 of the next 5 decades. In the table, the number 1 represents a decade with a flood. The numbers 2 through 5 represent a decade without a flood.
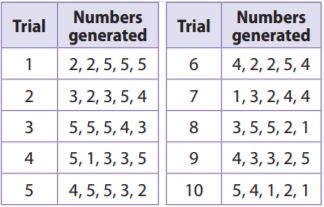
According to the simulation, what is the experimental probability of a flood in Bay City in at least 1 of the next 5 decades?
\(\frac{□}{□}\)
Answer: \(\frac{2}{5}\)
Explanation:
We have been given information about 10 trials and thus there are 10 possible outcomes.
possible outcomes = 10
The number 1 represents a decade with a flood. We then note that 4 of the 10 trials contained at least one 1 and thus there are 4 favorable outcomes.
favorable outcomes = 4
The probability is the number of favorable outcomes divided by the number of possible outcomes
P(Flood) = favorable outcomes/possible outcomes = 4/10 = \(\frac{2}{5}\)
Essential Question
Question 5.
How can you use theoretical probability to make predictions in real-world situations?
Type below:
______________
Answer:
You can use theoretical probabilities to make predictions by multiplying the theoretical probability times the number of events.
An example would be flipping a coin 50 times and wanting to predict the number of heads.
Since the theoretical probability of landing on heads is 1/2, a prediction is
50 × 1/2 = 25 heads.
Selected Response – Page No. 424
Question 1.
What is the probability of flipping two fair coins and having both show tails?
Options:
a. \(\frac{1}{8}\)
b. \(\frac{1}{4}\)
c. \(\frac{1}{3}\)
d. \(\frac{1}{2}\)
Answer: \(\frac{1}{4}\)
Explanation:
Each coin has 2 possible outcomes: Heads H and tails T
We then note that there are 4 possible outcomes for the 2 coins: HH, HT, TH, TT
Possible outcomes = 4
1 of the 4 possible outcomes results in two tails TT and thus there is 1 favorable outcome.
favorable outcomes = 1
The probability is the number of favorable outcomes divided by the number of possible outcomes
P(two tails) = favorable outcomes/possible outcomes = \(\frac{1}{4}\)
Thus the correct answer is option B.
Question 2.
A bag contains 8 white marbles and 2 black marbles. You pick out a marble, record its color, and put the marble back in the bag. If you repeat this process 45 times, how many times would you expect to remove a white marble from the bag?
Options:
a. 9
b. 32
c. 36
d. 40
Answer: 36
Explanation:
The bag contains 8 white marbles and 2 black marbles, which are thus 8 + 2 = 10 marbles in total and thus there are 10 possible outcomes.
possible outcomes = 10
We note that 8 of the marbles in the bag are white and thus there are 8 favorable outcomes.
favorable outcomes = 8
The probability is the number of favorable outcomes divided by the number of possible outcomes
P(white) = favorable outcomes/possible outcomes = \(\frac{8}{10}\) = \(\frac{4}{5}\)
The predicted number of times we select a white marble is then obtained by multiplying the number of repetitions by the probability.
Prediction = Number of repetitions × \(\frac{4}{5}\)
= 45 × \(\frac{4}{5}\)
= 9 × 4 = 36
Thus we predict that we will get a white marble about 36 times.
Thus the correct answer is option C.
Question 3.
Philip rolls a standard number cube 24 times. Which is the best prediction for the number of times he will roll a number that is even and less than 4?
Options:
a. 2
b. 3
c. 4
d. 6
Answer: 4
Explanation:
A number cube has 6 possible outcomes: 1, 2, 3, 4, 5, 6.
possible outcomes = 6
1 of the 6 possible outcomes results in an even number less than 4, that is the outcome 2.
favorable outcome = 1
The probability is the number of favorable outcomes divided by the number of possible outcomes
P(even and less than 4) = favorable outcomes/possible outcomes = 1/6
The predicted number of times we select an even number less than 4 is then obtained by multiplying the number of rolls by the probability.
Prediction = Number of rolls × P(even and less than 4)
= 24 × 1/6
= 4
Thus we predict that we roll an even number less than 4 about 4 times.
Thus the correct answer is option C.
Question 4.
A set of cards includes 24 yellow cards, 18 green cards, and 18 blue cards. What is the probability that a card chosen at random is not green?
Options:
a. \(\frac{3}{10}\)
b. \(\frac{4}{10}\)
c. \(\frac{3}{5}\)
d. \(\frac{7}{10}\)
Answer: \(\frac{7}{10}\)
Explanation:
The set of cards includes 24 yellow, 18 green and 18 blue cards, which are thus 24 + 18 + 18 = 60 cards in total and thus there are 60 possible outcomes.
possible outcomes = 60
18 of the 60 cards are green and thus 60 – 18 = 42 of the 60 cards are not green. This then implies that there are 42 favorable outcomes.
favorable outcomes = 42
The probability is the number of favorable outcomes divided by the number of possible outcomes
P(not green) = favorable outcomes/possible outcomes = 42/60 = \(\frac{7}{10}\)
Thus the correct answer is option D.
Question 5.
A rectangle made of square tiles measures 10 tiles long and 8 tiles wide. What is the width of a similar rectangle whose length is 15 tiles?
Options:
a. 3 tiles
b. 12 tiles
c. 13 tiles
d. 18.75 tiles
Answer: 12 tiles
Explanation:
Write the proportion relating to the lengths and widths of each rectangle.
length/width = 10/8 = 15/w
10w = 120
w = 12
Thus the correct answer is option B.
Question 6.
The Fernandez family drove 273 miles in 5.25 hours. How far would they have driven at that rate in 4 hours?
Options:
a. 208 miles
b. 220 miles
c. 280 miles
d. 358 miles
Answer: 208 miles
Explanation:
Write the proportion relating the number of miles and hours.
miles/hours = 273/5.25 = m/4
5.25m = 1092
m = 208 miles
Thus the correct answer is option A.
Question 7.
There are 20 tennis balls in a bag. Five are orange, 7 are white, 2 are yellow, and 6 are green. You choose one at random. Which color ball are you least likely to choose?
Options:
a. green
b. orange
c. white
d. yellow
Answer: yellow
Explanation:
The color with the fewest number of balls is yellow so you are least likely to choose yellow.
Thus the correct answer is option D.
Mini-Task
Question 8.
Center County has had a 1 in 6 (or about 16.7%) chance of a tornado in any given decade. In a simulation to consider the probability of tornadoes in the next 5 decades, Ava rolled a number cube. She let a 1 represent a decade with a tornado, and 2–6 represent decades without tornadoes. What experimental probability did Ava find for each event?
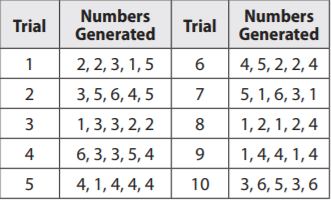
a. That Center County has a tornado in at least one of the next five decades.
\(\frac{□}{□}\)
Answer: \(\frac{3}{5}\)
Explanation:
We have been given the data about 10 trials and thus there are 10 possible outcomes.
possible outcomes = 10
The number 1 represents a tornado. We then note that 6 of the 10 trials contain at least one 1 and thus 6 of the 10 trials resulting in at least one tornado. This then implies that there are 6 favorable outcomes.
favorable outcomes = 6
The probability is the number of favorable outcomes divided by the number of possible outcomes
P(at least one tornado) = favorable outcomes/possible outcomes = 6/10 = \(\frac{3}{5}\)
Question 8.
b. That Center County has a tornado in exactly one of the next five decades
\(\frac{□}{□}\)
Answer: \(\frac{3}{10}\)
Explanation:
We have been given data about 10 trials and thus there are 10 possible outcomes.
possible outcomes = 10
The number 1 represents a tornado. We then note that 3 of the 10 trials contain at least one 1 and thus 3 of the 10 trials resulting in exactly one tornado. This then implies that there are 3 favorable outcomes.
favorable outcomes = 3
The probability is the number of favorable outcomes divided by the number of possible outcomes
P(exactly one tornado) = favorable outcomes/possible outcomes = 3/10 = 0.3
EXERCISES – Page No. 425
Find the probability of each event.
Question 1.
Rolling a 5 on a fair number cube.
\(\frac{□}{□}\)
Answer: \(\frac{1}{6}\)
Explanation:
A number cube has 6 possible outcomes: 1, 2, 3, 4, 5, 6
possible outcomes = 6
We note that 1 of the 6 possible outcomes results in a 5 and thus there is a favorable outcome.
favorable outcomes = 1
The probability is the number of favorable outcomes divided by the number of possible outcomes.
P(5) = favorable outcomes/possible outcomes
\(\frac{1}{6}\) ≈ 0.1667 = 16.67%
Question 2.
Picking a 7 from a standard deck of 52 cards. A standard deck includes 4 cards of each number from 2 to 10.
\(\frac{□}{□}\)
Answer: \(\frac{1}{13}\)
Explanation:
There are 52 cards in the standard deck of cards and thus there are 52 possible outcomes.
possible outcomes = 52
We note that 4 of the 52 cards are 7’s and thus there are 4 favorable outcomes.
favorable outcomes = 4
The probability is the number of favorable outcomes divided by the number of possible outcomes.
P(7) = favorable outcomes/possible outcomes
4/52 = \(\frac{1}{13}\) ≈ 0.0769 = 7.69%
Question 3.
Picking a blue marble from a bag of 4 red marbles, 6 blue marbles, and 1 white marble.
\(\frac{□}{□}\)
Answer: \(\frac{6}{11}\)
Explanation:
The bag contains 4 red, 6 blue, and 1 white marble, thus the bag contains 4 + 6 + 1 = 11 marbles in total and thus there are 11 possible outcomes.
possible outcomes = 11
We note that 6 of the 11 marbles in the bag are blue and thus there are 6 favorable outcomes.
favorable outcomes = 6
The probability is the number of favorable outcomes divided by the number of possible outcomes.
P(blue) = favorable outcomes/possible outcomes = \(\frac{6}{11}\) ≈ 0.5455 = 54.55%
Question 4.
Rolling a number greater than 7 on a 12-sided number cube.
\(\frac{□}{□}\)
Answer: \(\frac{5}{12}\)
Explanation:
A 12 side number cube has 12 possible outcomes: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12.
possible outcomes = 12
We note that 5 of the 12 possible outcomes result in a number greater than 7 (that is 8, 9, 10, 11, 12) and thus there are 5 favorable outcomes.
favorable outcomes = 5
The probability is the number of favorable outcomes divided by the number of possible outcomes:
P(Greater than 7) = favorable outcomes/possible outcomes = \(\frac{5}{12}\) ≈ 0.4167 = 41.67%
Page No. 426
Question 5.
Christopher picked coins randomly from his piggy bank and got the numbers of coins shown in the table. Find each experimental probability.
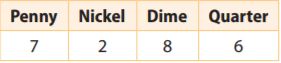
a. The next coin that Christopher picks is a quarter.
\(\frac{□}{□}\)
Answer: \(\frac{6}{23}\)
Explanation:
The table contains 7 pennies, 2 nickels, 8 dimes and 6 quarters, which are 7 + 2 + 8 + 6 = 23 coins in total and thus there are 23 possible outcomes.
possible outcomes = 23
We note that 6 of the 23 coins are quarters and thus there are 6 favorable outcomes.
favorable outcomes = 6
The probability is the number of favorable outcomes divided by the number of possible outcomes:
P(Quarter) = favorable outcomes/possible outcomes = \(\frac{6}{23}\) ≈ 0.2609 = 26.09%
Question 5.
b. The next coin that Christopher picks is not a quarter.
\(\frac{□}{□}\)
Answer: \(\frac{17}{23}\)
Explanation:
The sum of the probabilities of an event and its complement is always equal to 1.
P(not a Quarter) + P(Quarter) = 1
Let us then determine the probability of picking the marble that is not marked with the number 5.
P(not a Quarter) + P(Quarter) = 1
P(not a Quarter) = 1 – P(Quarter)
1 – \(\frac{6}{23}\)
= \(\frac{17}{23}\) ≈ 0.7391 = 73..91%
Question 5.
c. The next coin that Christopher picks is a penny or a nickel.
\(\frac{□}{□}\)
Answer: \(\frac{9}{23}\)
Explanation:
The table contains 7 pennies, 2 nickels, 8 dimes and 6 quarters, which are 7 + 2 + 8 + 6 = 23 coins in total and thus there are 23 possible outcomes.
possible outcomes = 23
There are 7 pennies and 2 nickels, thus 7 + 2 = 9 of the coins are pennies or nickels and thus there are 9 favorable outcomes.
favorable outcomes = 9
The probability is the number of favorable outcomes divided by the number of possible outcomes:
P(Penny or nickel) = favorable outcomes/possible outcomes = \(\frac{9}{23}\) ≈ 0.3913 = 39.13%
Question 6.
A grocery store manager found that 54% of customers usually bring their own bags. In one afternoon, 82 out of 124 customers brought their own grocery bags. Did a greater or lesser number of people than usual bring their own bags?
_____________
Answer: Greater
Explanation:
54% of 124 is 0.54 × 124 ≈ 67 so more customers than usual brought their own bag.
EXERCISES – Page No. 427
Find the probability of each event.
Question 1.
Graciela picks a white mouse at random from a bin of 8 white mice, 2 gray mice, and 2 brown mice.
\(\frac{□}{□}\)
Answer: \(\frac{2}{3}\)
Explanation:
There are 8 white, 2 gray, and 2 brown mice, thus there are 8 + 2 + 2 = 12 mice in total and thus there are 12 possible outcomes.
possible outcomes = 12
8 of the mice are white and thus there are 8 favorable outcomes
favorable outcomes = 8
The probability is the number of favorable outcomes divided by the number of possible outcomes:
P(white) = favorable outcomes/possible outcomes = \(\frac{8}{12}\) ≈ 0.6667 = 66.67%
Question 2.
Theo spins a spinner that has 12 equal sections marked 1 through 12. It does not land on 1.
\(\frac{□}{□}\)
Answer: \(\frac{11}{12}\)
Explanation:
There are 12 numbers from 1 to 12 and thus there are 12 possible outcomes.
possible outcomes = 12
11 of the 12 numbers from 1 to 12 are not 1 and thus there are 11 favorable outcomes
favorable outcomes = 11
The probability is the number of favorable outcomes divided by the number of possible outcomes:
P(not 1) = favorable outcomes/possible outcomes = \(\frac{11}{12}\) ≈ 0.9167 = 91.67%
Question 3.
Tania flips a coin three times. The coin lands on heads twice and on tails once, not necessarily in that order.
\(\frac{□}{□}\)
Answer: \(\frac{3}{8}\)
Explanation:
A fair coin has 2 possible outcomes: Heads and Tails T.
There are then 8 possible outcomes when tossing 3 coins: HHH, HHT, HTH, HTT, THH, THT, TTH, TTT.
possible outcomes = 8
We note that 3 of the possible outcomes result in two heads and one tail HHT, HTH, TTH and thus there are 3 favorable outcomes
favorable outcomes = 3
The probability is the number of favorable outcomes divided by the number of possible outcomes:
P(two heads and one tail) = favorable outcomes/possible outcomes = \(\frac{3}{8}\)
Question 4.
Students are randomly assigned two-digit codes. Each digit is either 1, 2, 3, or 4. Guy is given the number 11.
\(\frac{□}{□}\)
Answer: \(\frac{1}{16}\)
Explanation:
Each digit has 4 possible outcomes so there are 4 × 4 = 16 possible two-digit numbers with digits of 1, 2, 3 or 4. There is only one way to 11 as the two-digit number so the probability is \(\frac{1}{16}\)
Question 5.
Patty tosses a coin and rolls a number cube.
a. Find the probability that the coin lands on heads and the cube lands on an even number.
\(\frac{□}{□}\)
Answer:
A coin has 2 possible outcomes: heads H and tails T.
A number cube has 6 possible outcomes: 1, 2, 3, 4, 5, 6
We then note that there are 2 . 6 = 12 possible outcomes for the coin and the number cube: H1, H2, H3, H4, H5, H6, T1, T2, T3, T4, T5, T6
possible outcomes = 12
We then note that 3 of the 12 possible outcomes result in heads and an even number: H2, H4, H6.
favorable outcomes = 3
The probability is the number of favorable outcomes divided by the number of possible outcomes:
P(heads and even) = favorable outcomes/possible outcomes = \(\frac{3}{12}\) = \(\frac{1}{4}\)
Question 5.
b. Patty tosses the coin and rolls the number cube 60 times. Predict how many times the coin will land on heads and the cube will land on an even number.
______ times
Answer:
The predicted number of repetitions resulting in heads and an even number is then obtained by multiplying the number of repetitions by the probability.
Prediction = Number of repetitions × P
= 60 × \(\frac{1}{4}\)
= 15
Thus we predict taht we obtain heads with an even number about 15 times.
Question 6.
Rajan’s school is having a raffle. The school sold raffle tickets with 3-digit numbers. Each digit is either 1, 2, or 3. The school also sold 2 tickets with the number 000. Which number is more likely to be picked, 123 or 000?
____________
Answer: 000
Explanation:
There is only 1 ticket that has the number 123 and 2 tickets that have 000 so it is more likely that 000 will be picked.
Page No. 428
Question 7.
Suppose you know that over the last 10 years, the probability that your town would have at least one major storm was 40%. Describe a simulation that you could use to find the experimental probability that your town will have at least one major storm in at least 3 of the next 5 years.
Type below:
____________
Answer:
Since the probability is 40% = 4/10 = 2/5, randomly generate numbers from 1 to 5 where 1 and 2 is a year with a major storm and 3 to 5 is a year without a major storm.
Unit 6 Performance Tasks
Question 8.
Meteorologist
A meteorologist predicts a 20% chance of rain for the next two nights and a 75% chance of rain on the third night.
a. On which night is it most likely to rain? On that night, is it likely to rain or unlikely to rain?
Type below:
____________
Answer: 3rd night
Explanation:
The third night it is most likely to rain since the probability of rain is higher that night. Since the probability of 75% is greater than 50%, it is likely that it will rain.
Question 8.
b. Tara would like to go camping for the next 3 nights, but will not go if it is likely to rain on all 3 nights. Should she go? Use probability to justify your answer.
Type below:
____________
Answer:
The probability that it will rain all three nights is 0.2 × 0.2 × 0.75 = 0.03 = 3%. It is unlikely that it will rain all 3 nights since the probability is 3% so she should go.
Question 9.
Sinead tossed 4 coins at the same time. She did this 50 times, and 6 of those times, all 4 coins showed the same result (heads or tails).
a. Find the experimental probability that all 4 coins show the same result when tossed.
\(\frac{□}{□}\)
Answer: \(\frac{3}{25}\)
Explanation:
The 4 coins were tossed 50 times and thus there are 50 possible outcomes.
possible outcomes = 50
The result showed that all 4 coins have the same result on 6 of the 50 tosses.
favorable outcomes = 6
The probability is the number of favorable outcomes divided by the number of possible outcomes:
P(Same result) = favorable outcomes/possible outcomes = \(\frac{6}{50}\) = \(\frac{3}{25}\)
Question 9.
b. Can you determine the experimental probability that no coin shows heads? Explain.
Type below:
____________
Answer:
The 4 coins were tossed 50 times and thus there are 50 possible outcomes.
possible outcomes = 50
The probability is the number of favorable outcomes divided by the number of possible outcomes:
P(No heads) = favorable outcomes/possible outcomes
Since we know the number of possible outcomes, we require the knowledge of the number of favorable outcomes to determine the probability.
That is, we require the knowledge of how many of the tosses resulted in no heads. Since this has not been given, we cannot determine the experimental probability that no coin show heads.
Question 9.
c. Suppose Sinead tosses the coins 125 more times. Use experimental probability to predict the number of times that all 4 coins will show heads or tails. Show your work.
_______ times
Answer:
The predicted number of times that all 4 coins will show heads or tails is then obtained by multiplying the number of times by the probability.
Since the coins were tossed 50 times initially and now were tossed 125 more times, the coins were tossed 50 + 125 = 175 times in total.
Prediction = Number of times × P
= 175 × \(\frac{3}{25}\)
= 7 × 3 = 21
Thus we predict that we obtain that all 4 coins will show heads or tails about 21 times.
Selected Response – Page No. 429
Question 1.
A pizza parlor offers thin, thick, and traditional style pizza crusts. You can get pepperoni, beef, mushrooms, olives, or peppers for toppings. You order a one-topping pizza. How many outcomes are in the sample space?
Options:
a. 3
b. 5
c. 8
d. 15
Answer: 15
Explanation:
The Fundamental Counting Principle (also called the counting rule) is a way to figure out the number of outcomes in a probability problem. Basically, you multiply the events together to get the total number of outcomes.
Crust: 3 ways (thin, thick, traditional)
Topping: 5 ways (pepperoni, beef, mushrooms, olives, peppers)
Use the Fundamental Counting Principle:
3 × 5 = 15
Thus there are 15 possible outcomes in the sample space.
Thus the correct answer is option D.
Question 2.
A bag contains 9 purple marbles, 2 blue marbles, and 4 pink marbles. The probability of randomly drawing a blue marble is \(\frac{2}{15}\). What is the probability of not drawing a blue marble?
Options:
a. \(\frac{2}{15}\)
b. \(\frac{4}{15}\)
c. \(\frac{11}{15}\)
d. \(\frac{13}{15}\)
Answer: \(\frac{13}{15}\)
Explanation:
Given,
P(blue) = \(\frac{2}{15}\)
The sum of the probabilities of an event and its complement is always equal to 1.
P(not blue) + P(blue) = 1
Let us determine the probability of picking the marble that is not marked with the number 5.
P(not blue) = 1 – P(blue)
= 1 – \(\frac{2}{15}\)
= \(\frac{15}{15}\) – \(\frac{2}{15}\)
= \(\frac{13}{15}\)
Thus the correct answer is option D.
Question 3.
During the month of April, Dora kept track of the bugs she saw in her garden. She saw a ladybug on 23 days of the month. What is the experimental probability that she will see a ladybug on May 1?
Options:
a. \(\frac{1}{23}\)
b. \(\frac{7}{30}\)
c. \(\frac{1}{2}\)
d. \(\frac{23}{30}\)
Answer: \(\frac{23}{30}\)
Explanation:
There are 30 days in the month of April and thus there are 30 possible outcomes.
possible outcomes = 30
A ladybug was seen on 23 of the 30 days and thus there are 23 favorable outcomes.
favorable outcomes = 23
The probability is the number of favorable outcomes divided by the number of possible outcomes:
P(see ladybug) = favorable outcomes/possible outcomes = \(\frac{23}{30}\)
Thus the correct answer is option D.
Question 4.
Ryan flips a coin 8 times and gets tails all 8 times. What is the experimental probability that Ryan will get heads the next time he flips the coin?
Options:
a. 1
b. \(\frac{1}{2}\)
c. \(\frac{1}{8}\)
d. 0
Answer: 0
Explanation:
The coin was flipped 8 times and thus there are 8 possible outcomes.
possible outcomes = 5
All 8 flips resulted in tails and thus heads occurred on 0 of the flips, which implies that there are 0 favorable outcomes.
favorable outcomes = 0
The probability is the number of favorable outcomes divided by the number of possible outcomes:
P(heads) = favorable outcomes/possible outcomes = \(\frac{0}{8}\) = 0
Thus the correct answer is option D.
Question 5.
A used guitar is on sale for $280. Derek offers the seller \(\frac{3}{4}\) of the advertised price. How much does Derek offer for the guitar?
Options:
a. $180
b. $210
c. $240
d. $270
Answer: $210
Explanation:
Since 280(3/4) = 210, he offered $210 for the guitar.
Thus the correct answer is option B.
Question 6.
Jay tossed two coins several times and then recorded the results in the table below
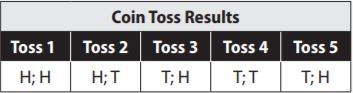
What is the experimental probability that the coins will land on different sides on his next toss?
Options:
a. \(\frac{1}{5}\)
b. \(\frac{2}{5}\)
c. \(\frac{3}{5}\)
d. \(\frac{4}{5}\)
Answer: \(\frac{3}{5}\)
Explanation:
We have the coin toss results of 5 tosses and thus there are 5 possible outcomes.
possible outcomes = 5
Wwe note that 3 of the 5 tosses resulted in two different sides (H, T or T, H) and thus there are 3 favorable outcomes.
The probability is the number of favorable outcomes divided by the number of possible outcomes:
P(different sides) = favorable outcomes/possible outcomes = \(\frac{3}{5}\)
Thus the correct answer is option C.
Question 7.
What is the probability of tossing two fair coins and having exactly one land tails side up?
Options:
a. \(\frac{1}{8}\)
b. \(\frac{1}{4}\)
c. \(\frac{1}{3}\)
d. \(\frac{1}{2}\)
Answer: \(\frac{1}{2}\)
Explanation:
Each coin has 2 possible outcomes: Heads H and Tails T.
When tossing 2 fair coins, then there are 4 possible outcomes: HH, HT, TH, TT.
possible outcomes = 4
We note that 2 of the 4 possible outcomes result in exactly one tail (TH or HT) and thus there are 2 favorable outcomes.
favorable outcomes = 2
The probability is the number of favorable outcomes divided by the number of possible outcomes:
P(exacly one tail) = favorable outcomes/possible outcomes = \(\frac{2}{4}\) = \(\frac{1}{2}\)
Thus the correct answer is option D.
Question 8.
Find the percent change from 60 to 96.
Options:
a. 37.5% decrease
b. 37.5% increase
c. 60% decrease
d. 60% increase
Answer: 60% increase
Explanation:
Percent change = (amount of change)/(original amount).
The amount of change is 96 – 60 = 36 and the original amount is 60.
The percent change is then 36/60 = 0.6 = 60%.
Since the amounts got larger, it is an increase.
Thus the correct answer is option D.
Question 9.
A bag contains 6 white beads and 4 black beads. You pick out a bead, record its color, and put the bead back in the bag. You repeat this process 35 times. Which is the best prediction of how many times you would expect to remove a white bead from the bag?
Options:
a. 6
b. 10
c. 18
d. 21
Answer: 21
Explanation:
The bag contains 6 white and 4 black beads, which are thus 6 + 4 = 10 beads in total and thus there are 10 favorable outcomes.
possible outcomes = 10
6 of the 10 beads are white and thus there are 6 favorable outcomes.
favorable outcomes = 6
The probability is the number of favorable outcomes divided by the number of possible outcomes:
P(white) = favorable outcomes/possible outcomes = 6/10 = 3/5 = 0.6 = 60%
The predicted number of selected white beads is then obtained by multiplying the number of repetitions by the probability.
Prediction = Number of repetitions × P(white)
35 × 6/10
= 210/10
= 21
Thus we predict that we removed 21 white beads from the bag.
Thus the correct answer is option D.
Question 10.
A set of cards includes 20 yellow cards, 16 green cards, and 24 blue cards. What is the probability that a blue card is chosen at random?
Options:
a. 0.04
b. 0.24
c. 0.4
d. 0.66
Answer: 0.4
Explanation:
There are 20 yellow, 16 green and 24 blue cards, which are thus 20 + 16 + 21 = 60 cards and thus there are 60 possible outcomes.
possible outcomes = 60
24 of the 60 cards are blue and thus there are 24 favorable outcomes.
favorable outcomes = 24
The probability is the number of favorable outcomes divided by the number of possible outcomes:
P(blue) = favorable outcomes/possible outcomes = \(\frac{24}{60}\) = \(\frac{2}{5}\)
Thus the correct answer is option C.
Page No. 430
Question 11.
Jason, Erik, and Jamie are friends in art class. The teacher randomly chooses 2 of the 21 students in the class to work together on a project. What is the probability that two of these three friends will be chosen?
Options:
a. \(\frac{1}{105}\)
b. \(\frac{1}{70}\)
c. \(\frac{34}{140}\)
d. \(\frac{4}{50}\)
Answer: \(\frac{1}{70}\)
Explanation:
The probability that one of the friends is chosen as the first student is 3/21 = 1/7 since there are 3 friends and 21 total students.
The probability that a second friend is chosen is then 2/20 = 1/10 since there are 2 remaining friends and a total of 20 remaining students.
The probability that two friends is chosen is then (1/7)(1/10) = \(\frac{1}{70}\)
Thus the correct answer is option B.
Question 12.
Philip rolls a number cube 12 times. Which is the best prediction for the number of times that he will roll a number that is odd and less than 5?
Options:
a. 2
b. 3
c. 4
d. 6
Answer: 4
Explanation:
A number cube has 6 possible outcomes: 1, 2, 3, 4, 5, 6
possible outcomes = 6
2 of the 6 possible outcomes are odd and less than 5
favorable outcomes = 2
The probability is the number of favorable outcomes divided by the number of possible outcomes:
P(odd and less than 5) = favorable outcomes/possible outcomes = \(\frac{2}{6}\) = \(\frac{1}{3}\)
The predicted number of odd numbers less than 5 that is rolled is then obtained by multiplying the number of rolls by the probability.
Prediction = Number of rolls × P(odd and less than 5)
= 12 × \(\frac{1}{3}\)
= 4
Thus 4 of the trolls are expected to result in an odd number less than 5.
Thus the correct answer is option C.
Question 13.
A survey reveals that one airline’s flights have a 92% probability of being on time. Based on this, out of 4000 flights in a year, how many flights would you predict will arrive on time?
Options:
a. 368
b. 386
c. 3680
d. 3860
Answer: 3680
Explanation:
Given,
P(on time) = 92% = 0.92
The predicted number of flights that arrive on time is then obtained by multiplying the number of flights by the probability.
Prediction = Number of flights × P(on time)
= 4000 × 0.92
= 3680
Thus we predict that about 3680 of the flights are on time.
Thus the correct answer is option C.
Question 14.
Matt’s house number is a two-digit number. Neither of the digits is 0 and the house number is even. What is the probability that Matt’s house number is 18?
Options:
a. \(\frac{1}{45}\)
b. \(\frac{1}{36}\)
c. \(\frac{1}{18}\)
d. \(\frac{1}{16}\)
Answer: \(\frac{1}{36}\)
Explanation:
The Fundamental Counting Principle (also called the counting rule) is a way to figure out the number of outcomes in a probability problem. Basically, you multiply the events together to get the total number of outcomes.
There are 9 digits excluding 0 (1, 2, 3, 4, 5, 6, 7, 8, 9) and there are 4 even digits excluding 0 (2, 4, 6, 8). By the fundamental counting principle, there are then 9 . 4 =36 two digit numbers that do not contain a 0 and that are even. Thus there are 36 possible outcomes.
possible outcomes = 36
18 is 1 of the 36 possible outcomes and thus there is 1 favorable outcome.
favorable outcomes = 1
The probability is the number of favorable outcomes divided by the number of possible outcomes:
P(blue) = favorable outcomes/possible outcomes = \(\frac{1}{36}\)
Thus the correct answer is option B.
Mini-Tasks
Question 15.
Laura picked a crayon randomly from a box, recorded the color, and then placed it back in the box. She repeated the process and recorded the results in the table.

Find each experimental probability. Write your answers in simplest form.
a. The next crayon Laura picks is red.
\(\frac{□}{□}\)
Answer:
There are 5 red, 6 blue, 7 yellow and 2 green crayons, which are thus 5 + 6 + 7 + 2 = 20 crayons in total and thus there are 20 possible outcomes.
possible outcomes = 20
5 of the 20 crayons are red and thus there are 5 favorable outcomes.
favorable outcomes = 5
The probability is the number of favorable outcomes divided by the number of possible outcomes:
P(red) = favorable outcomes/possible outcomes = \(\frac{5}{20}\) = \(\frac{1}{4}\)
Question 15.
b. The next crayon Laura picks is not red.
\(\frac{□}{□}\)
Answer:
The sum of the probabilities of an event and its complement is always equal to 1.
P(not red) + P(red) = 1
Let us then determine the probability of picking the marble that is not marked with the number 5.
P(not red) = 1 – P(red)
= 1 – 1/4
= 3/4
Question 16.
For breakfast, Trevor has a choice of 3 types of bagels (plain, sesame, or multigrain), 2 types of eggs (scrambled or poached), and 2 juices (orange or apple).
a. Use the space below to make a tree diagram to find the sample space.
Type below:
_____________
Answer:
There are 3 types of bagels and thus we draw a root with 3 possible children labeled plain, sesame, and multigrain.
There are 2 types of eggs, thus we draw 2 children for each of the 3 previous children and label these two children as scrambled and poached.
There are 2 juices, thus we draw 2 children for each of the 2 previous children and label these two children as orange or apple.
Question 16.
b. If he chooses at random, what is the probability that Trevor eats a breakfast that has orange juice?
\(\frac{□}{□}\)
Answer: \(\frac{1}{2}\)
Explanation:
The bottom row of the tree diagram of part (a) contains 12 elements and thus there are 12 possible outcomes.
possible outcomes = 12
6 of the labels in the bottom row are “orange” and thus there are 6 favorable outcomes.
favorable outcomes = 6
The probability is the number of favorable outcomes divided by the number of possible outcomes:
P(orange juice) = favorable outcomes/possible outcomes = \(\frac{6}{12}\) = \(\frac{1}{2}\)
Conclusion:
In this lesson, we will look into experimental probability and theoretical probability. The solutions prepared in this chapter are made by the math experts. So, refer to the Go Math Grade 7 Answer Key Chapter 13 Theoretical Probability and Simulations while practicing for the exams. Follow our Go Math Answer Key to get the step by step explanation for all the chapters of 7th grade.
