Boost your math skills by referring to the Go Math Grade 4 Answer Key Homework FL Chapter 6 Fraction Equivalence and Comparison Review/Test. With the support of this HMH Go Math Grade 4 Review/Test Answer Key you score good marks in the exam.
Go Math Grade 4 Answer Key Homework FL Chapter 6 Fraction Equivalence and Comparison Review/Test
Go Math Grade 4 Answer Key Homework FL Review/Test covers all the topics in Chapter 6 Fraction Equivalence and Comparison. Explore the knowledge of your child by giving the question from Review/Test. Just hit on the link and download it. Go Math Grade 4 Answer Key Homework FL Chapter 6 Fraction Equivalence and Comparison Review/Test.
Chapter 6: Review/Test
- Review/Test – Page No. 261
- Review/Test – Page No. 262
- Review/Test – Page No. 263
- Review/Test – Page No. 264
Review/Test – Page No. 261
Choose the best term from the box.
Question 1.
A ________________ is a common multiple of two or more denominators.
________
Answer:
A common denominator is a common multiple of two or more denominators..
Question 2.
A fraction is in _________________ when the numerator and denominator have only 1 as a common factor
________
Answer:
A fraction is in simplest form when the numerator and denominator have only 1 as a common factor.
Question 3.
A ________________ is a known size or amount that helps you understand another size or amount.
________
Answer:
A benchmark is a known size or amount that helps you understand another size or amount.
Write two equivalent fractions.
Question 4.
\(\frac{4}{6}\)
Answer: \(\frac{6}{9}\) and \(\frac{8}{12}\).
Explanation:
To find equivalent fractions we will multiply its numerator and denominator by the same number. Firstly we will calculate GCF for the given fraction i.e \(\frac{4}{6}\), the GCF for (4,6) is 2. As GCF is not equal to 1, we will divide the numerator and denominator by 2. By dividing with 2 we will get the fraction as \(\frac{2}{3}\). Now we will multiply the numerator and denominator with 3,
So the fraction will be 3(\(\frac{2}{3}\))
= \(\frac{6}{9}\). For the second equivalent fraction, we will multiply numerator and denominator with 4,
So the fraction will be 4(\(\frac{2}{3}\))
= \(\frac{8}{12}\).
So, the two equivalent fractions of \(\frac{4}{6}\) are \(\frac{6}{9}\) and \(\frac{8}{12}\).
Question 5.
\(\frac{6}{10}\)
Answer: \(\frac{9}{15}\) and \(\frac{12}{20}\).
Explanation:
To find equivalent fractions we will multiply its numerator and denominator by the same number. Firstly we will calculate GCF for the given fraction i.e \(\frac{6}{10}\), the GCF for (6,10) is 2. As GCF is not equal to 1, we will divide the numerator and denominator by 2. By dividing with 2 we will get the fraction as \(\frac{3}{5}\). Now we will multiply the numerator and denominator with 3,
So the fraction will be 3(\(\frac{3}{5}\))
= \(\frac{9}{15}\). For the second equivalent fraction, we will multiply numerator and denominator with 4,
So the fraction will be 4(\(\frac{3}{5}\))
= \(\frac{12}{20}\).
So, the two equivalent fractions of \(\frac{3}{5}\) are \(\frac{9}{15}\) and \(\frac{12}{20}\).
Question 6.
\(\frac{2}{8}\)
Answer: \(\frac{3}{12}\) and \(\frac{4}{16}\).
Explanation:
To find equivalent fractions we will multiply its numerator and denominator by the same number. Firstly we will calculate GCF for the given fraction i.e \(\frac{2}{8}\), the GCF for (2,8) is 2. As GCF is not equal to 1, we will divide the numerator and denominator by 2. By dividing with 2 we will get the fraction as \(\frac{1}{4}\). Now we will multiply the numerator and denominator with 3,
So the fraction will be 3(\(\frac{1}{4}\))
= \(\frac{3}{12}\). For the second equivalent fraction, we will multiply numerator and denominator with 4,
So the fraction will be 4(\(\frac{1}{4}\))
= \(\frac{4}{16}\).
So, the two equivalent fractions of \(\frac{2}{8}\) are \(\frac{3}{12}\) and \(\frac{4}{16}\).
Write each pair of fractions as a pair of fractions with a common denominator.
Question 7.
\(\frac{3}{4} \text { and } \frac{7}{8}\)
Answer: \(\frac{6}{8}\) , \(\frac{7}{8}\).
Explanation:
To get the common denominators we will multiply \(\frac{3}{4}\) with 2, so that the fraction will be \(\frac{6}{8}\). As the other fraction is \(\frac{7}{8}\). So the denominators are the same.
Question 8.
\(\frac{2}{3} \text { and } \frac{1}{4}\)
Answer: \(\frac{8}{12}\) and \(\frac{3}{12}\).
Explanation:
To get the common denominators we will multiply \(\frac{2}{3}\) with 4 and \(\frac{1}{4}\) with 3, so that the fractions will be \(\frac{8}{12}\) and \(\frac{3}{12}\). So the denominators are same.
Question 9.
\(\frac{7}{10} \text { and } \frac{4}{5}\)
Answer: \(\frac{7}{10}\) and \(\frac{8}{10}\).
Explanation:
To get the common denominators we will multiply \(\frac{4}{5}\) with 2, so that the fraction will be \(\frac{8}{10}\). As the other fraction is \(\frac{7}{10}\). And the denominators are same.
Compare. Write <, >, or 5.
Question 10.
\(\frac{5}{8}\) _____ \(\frac{5}{12}\)
Answer: \(\frac{5}{8}\) > \(\frac{5}{12}\).
Explanation:
To compare \(\frac{5}{8}\) and \(\frac{5}{12}\) first we will find LCM of 8 and 12.
And the LCM of (8,12) is 24. Now we will multiply \(\frac{5}{8}\) with 3 and \(\frac{5}{12}\) with 2, so the fraction will be \(\frac{15}{24}\) and the other fraction is \(\frac{10}{24}\).
So \(\frac{15}{24}\) is greater than \(\frac{10}{24}\).
Question 11.
\(\frac{10}{12}\) _____ \(\frac{5}{6}\)
Answer: \(\frac{10}{12}\) = \(\frac{5}{6}\).
Explanation:
To compare \(\frac{10}{12}\) and \(\frac{5}{6}\),first we will find LCM of 12 and 6.
And the LCM of (12,6) is 12. Now we will multiply \(\frac{5}{6}\) with 2, so the fraction will be \(\frac{10}{12}\) and the other fraction is \(\frac{10}{12}\).
So \(\frac{10}{12}\) is equal to \(\frac{10}{12}\).
Question 12.
\(\frac{1}{2}\) _____ \(\frac{3}{10}\)
Answer: \(\frac{1}{2}\) > \(\frac{3}{10}\).
Explanation:
To compare \(\frac{1}{2}\) and \(\frac{3}{10}\) first we will find LCM of 2 and 10.
And the LCM of (2,10) is 10. Now we will multiply \(\frac{1}{2}\) with 5, so the fraction will be \(\frac{5}{10}\) and the other fraction is \(\frac{3}{10}\).
So \(\frac{5}{10}\) is greater than \(\frac{3}{10}\).
Question 13.
\(\frac{1}{4}\) _____ \(\frac{1}{3}\)
Answer: \(\frac{1}{4}\) < \(\frac{1}{3}\).
Explanation:
To compare \(\frac{1}{4}\) and \(\frac{1}{3}\) first we will find LCM of 4 and 3.
And the LCM of (4,3) is 12. Now we will multiply \(\frac{1}{4}\) with 3 and \(\frac{1}{3}\) with 4, so the fraction will be \(\frac{3}{12}\) and the other fraction is \(\frac{4}{12}\).
So \(\frac{3}{12}\) is less than \(\frac{4}{12}\).
Write the fractions in order from least to greatest.
Question 14.
\(\frac{2}{3}, \frac{3}{4}, \frac{1}{6}\)
Answer: \(\frac{1}{6}\) < \(\frac{2}{3}\)< \(\frac{3}{4}\).
Explanation:
To write the fraction from least to greatest we will find LCM of 3,4,6. And the LCM of (3,4,6) is 12. Now we will multiply
\(\frac{2}{3}\) with 4 and \(\frac{3}{4}\) with 3 and \(\frac{1}{6}\) with 2, so the fraction will be
\(\frac{8}{12}\) and \(\frac{9}{12}\), \(\frac{2}{12}\)
So \(\frac{2}{12}\) is less than \(\frac{8}{12}\) is less than \(\frac{9}{12}\).
Question 15.
\(\frac{7}{10}, \frac{4}{5}, \frac{1}{2}, \frac{4}{12}\)
Answer: \(\frac{4}{12}\) < \(\frac{1}{2}\)< \(\frac{7}{10}\)< \(\frac{4}{5}\).
Explanation:
To write the fraction from least to greatest we will find LCM of 10,5,2,12. And the LCM of (10,5,2,12) is 60. Now we will multiply
\(\frac{7}{10}\) with 6 and \(\frac{4}{5}\) with 12 and \(\frac{1}{2}\) with 30 and \(\frac{4}{12}\) with 5 , so the fraction will be
\(\frac{42}{60}\) and \(\frac{48}{60}\), \(\frac{30}{60}\), \(\frac{20}{60}\)
So \(\frac{20}{60}\) is less than \(\frac{30}{60}\) is less than \(\frac{42}{60}\) is less than
\(\frac{48}{60}\).
Review/Test – Page No. 262
Fill in the bubble completely to show your answer.
Question 16.
Paco needs at least \(\frac{3}{8}\) yard of twine to build a model ship. How much twine could he buy?
Options:
a. \(\frac{3}{10}\) yard
b. \(\frac{1}{4}\) yard
c. \(\frac{3}{5}\) yard
d. \(\frac{1}{8}\) yard
Answer: c.
Explanation:
a) 3/10 yard. As we know that for two rational numbers with the same numerator but with different denominators the number whose denominator is smaller is a greater quantity.
Hence 3/10 < 3/8. And option a is incorrect.
b) 1/4 yard. As to compare to rational numbers we have to either make the numerator equal or their denominator equal. Hence here we multiply and divide 1/4 by 2 to get 8 in the denominator. As 2/8 < 3/8
since the denominator is the same and the number with the same denominator but with different numerators are compared as whose numerator is greater is a greater quantity. And the option b is incorrect.
c) 3/4 yard. As both the numbers have the same numerator but different denominator and we know that for two rational numbers with the same numerator but with different denominators the number whose denominator is smaller is a greater quantity. As 3/8 < 3/4, so option c is correct.
d) 1/8 yard. As both the numbers have the same denominator and we know that for two rational numbers with the same denominator but with the different numerators, the number whose numerator is smaller is a smaller quantity. So 1/8 < 3/8 and the option d is incorrect.
Question 17.
Rachel, Nancy, and Diego were in a fishing competition. Rachel’s fish was \(\frac{7}{8}\) foot long, Nancy’s fish was \(\frac{1}{4}\) foot long, and Diego’s fish was \(\frac{1}{2}\) foot long. What are the lengths of the fish in order from least to greatest?
Options:
a. \(\frac{7}{8}\) foot, \(\frac{1}{2}\) foot, \(\frac{1}{4}\) foot
b. \(\frac{1}{2}\) foot, \(\frac{7}{8}\) foot, \(\frac{1}{4}\) foot
c. \(\frac{7}{8}\) foot, \(\frac{1}{4}\) foot, \(\frac{1}{2}\) foot
d. \(\frac{1}{4}\) foot, \(\frac{1}{2}\) foot, \(\frac{7}{8}\) foot
Answer: d
Explanation:
As Rachel’s fish was \(\frac{7}{8}\) foot long, Nancy’s fish was \(\frac{1}{4}\) foot long, Diego’s fish was \(\frac{1}{2}\) foot long, so to find the lengths of the fish in order from least to greatest we will find the LCM of (8,4,2), so the LCM of (8,4,2) is 8 and we will multiply \(\frac{1}{4}\) with 2 and \(\frac{1}{2}\) with 4, so the fraction will be \(\frac{2}{8}\) and \(\frac{4}{8}\). The lengths of the fish in order from least to greatest are \(\frac{2}{8}\), latex]\frac{4}{8}[/latex], latex]\frac{7}{8}[/latex]
Question 18.
Amy needs \(\frac{6}{8}\) gallon of fruit juice to make punch. She needs an equal amount of sparkling water. How much sparkling water does she need?
Options:
a. \(\frac{2}{8}\) gallon
b. \(\frac{1}{2}\) gallon
c. \(\frac{2}{3}\) gallon
d. \(\frac{3}{4}\) gallon
Answer: d
Explanation:
Amy needs \(\frac{6}{8}\) gallon of fruit juice to make punch and she needs an equal amount of sparkling water, so Amy needs \(\frac{6}{8}\) or \(\frac{3}{4}\) gallon.
Question 19.
Gavin is building a model of a kitchen. In the model, \(\frac{2}{5}\) of the floor tiles are white, \(\frac{1}{2}\) of the floor tiles are yellow, and \(\frac{1}{10}\) of the floor tiles are brown. How many floor tiles could be in the model?
Options:
a. 2
b. 5
c. 10
d. 17
Answer: c
Explanation:
As Gavin is building a model of a kitchen and \(\frac{2}{5}\) of the floor tiles are white, \(\frac{1}{2}\) of the floor tiles are yellow, and \(\frac{1}{10}\) of the floor tiles are brown. To find the total number of tiles we will add up all color tiles. For that, we will multiply \(\frac{1}{2}\) with 5 and \(\frac{2}{5}\) with 2 to set the denominators equal. Then the fractions will be \(\frac{5}{10}\) and \(\frac{4}{10}\). Now add all three
\(\frac{5}{10}\)+\(\frac{4}{10}\)+\(\frac{1}{10}\)
= 10.
So the number of floor tiles modeled is 10
Review/Test – Page No. 263
Fill in the bubble completely to show your answer.
Question 20.
Bill has enough money to buy no more than \(\frac{1}{2}\) pound of cheese. How much cheese could he buy?
Options:
a. \(\frac{1}{3}\) pound
b. \(\frac{4}{6}\) pound
c. \(\frac{5}{8}\) pound
d. \(\frac{3}{4}\) pound
Answer: a
Explanation:
As Bill has enough money to buy no more than \(\frac{1}{2}\) pound of cheese, so he needs to buy \(\frac{1}{3}\) pounds.
Question 21.
Students planted 6 equal-size gardens on Earth Day. They divided each garden into 3 equal sections and planted herbs in 2 of the 3 sections. What fraction of the gardens did the students plant with herbs?
Options:
a. \(\frac{3}{6}\)
b. \(\frac{2}{6}\)
c. \(\frac{6}{18}\)
d. \(\frac{12}{18}\)
Answer: d
Explanation:
As students planted 6 equal-size gardens on Earth Day, and they divided each garden into 3 equal sections and planted herbs in 2 of the 3 sections, so the fraction of the gardens did the students plant with herbs are we need to multiply 6×3 and will get 18 sections in all gardens, then we need to multiply 2×6 and get 12 sections are herbs. So, 12 out of 18 are herbs i.e \(\frac{12}{18}\).
Question 22.
Noah and Leslie live the same distance from school. Which could be the distances they live from school?
Options:
a. \(\frac{7}{100}\) kilometer and \(\frac{7}{10}\) kilometer
b. \(\frac{5}{10}\) kilometer and \(\frac{1}{5}\) kilometer
c. \(\frac{80}{100}\) kilometer and \(\frac{8}{10}\) kilometer
d. \(\frac{6}{10}\) kilometer and \(\frac{2}{5}\) kilometer
Answer: c.
Explanation:
The option c is correct, as \(\frac{80}{100}\) km is equal to \(\frac{8}{10}\) when it is reduced.
Question 23.
Keiko needs \(\frac{8}{12}\) yard of fabric to finish her quilt. What is \(\frac{8}{12}\) written in simplest form?
Options:
a. \(\frac{4}{6}\)
b. \(\frac{2}{3}\)
c. \(\frac{3}{4}\)
d. \(\frac{1}{2}\)
Answer: b
Explanation:
As Keiko needs \(\frac{8}{12}\) yard of fabric to finish her quilt and the simplest form of \(\frac{8}{12}\) is \(\frac{2}{3}\).
Review/Test – Page No. 264
Question 24.
Sam needs \(\frac{4}{6}\) cup of laundry detergent for his laundry. The cap on top of the laundry detergent holds \(\frac{1}{3}\) cup. He has 1 capful of detergent. Does he have enough? Explain.
Answer: Sam does not have enough.
Explanation:
As Sam needs \(\frac{4}{6}\) cup of laundry detergent for his laundry and the cap holds only \(\frac{1}{3}\) and Sam has 1 capful of detergent, and Sam needs 2 cups instead of 1 cup because \(\frac{4}{6}\) is equivalent to \(\frac{2}{3}\) and Sam only has \(\frac{1}{3}\) cup, so he needs 2 cups.
Question 25.
The table shows the distances of some places in town from the school.
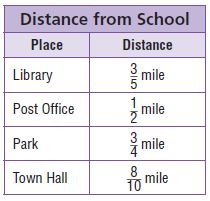
A. Are any of the places shown in the table closer than \(\frac{1}{2}\) mile to school? Explain how you know.
Answer: Library \(\frac{3}{5}\) mile.
Explanation:
To find which place is closer, we will find the LCM of the denominators i.e (5,2,4,10). And the LCM of (5,2,4,10) is 20, so we will divide \(\frac{3}{5}\) with 4, \(\frac{1}{2}\) with 10, \(\frac{3}{4}\) with 5 and \(\frac{8}{10}\) with 2. So that the fractions will have same denominators and we can find easily which place is closer. And the fractions after multiplying are \(\frac{12}{20}\), \(\frac{10}{20}\), \(\frac{15}{20}\) and \(\frac{16}{20}\). So the places closer than \(\frac{1}{2}\) mile to school are post office which is \(\frac{10}{20}\) mile and next place is library which is \(\frac{12}{20}\) mile.
Question 25.
B. Are any of the places shown in the table the same distance from school? Explain how you know.
Answer: Yes.
Question 25.
C. Which place is farthest from school? Explain.
Answer: Townhall.
Explanation:
Townhall is the farthest from the school as it’s distance is \(\frac{8}{10}\) mile.
Conclusion:
The students of 4th grade can check all chapters in Go Math Grade Answer Key in pdf format so that your learning will kick start in an effective manner. We have given a brief explanation of each and every question on our Go Math Grade 4 Answer Key Homework FL Chapter 6 Fraction Equivalence and Comparison Review/Test. We suggest the students understand the concepts and apply them in the real world.
