Go Math Grade 4 Chapter 13 Answer Key Pdf: Hello students!!! Are you searching for the Grade 4 Answer Key of Go Math Chapter 13 Algebra: Perimeter and Area. Then what are you waiting for Download Go Math Grade 4 Answer Key Chapter 13 Algebra: Perimeter and Area pdf for free of cost here. Make our Go Math Grade 4 Chapter 13 Solution Key as a reference while practicing for your exams. Check out the topics covered in Go Math Grade 4 Answer Key Chapter 13 Algebra: Perimeter and Area from the below.
Algebra: Perimeter and Area Go Math Grade 4 Chapter 13 Answer Key Pdf
Students can get the solution for only for the exercises and homework problems but also for the Mid-Chapter checkpoint and review test. So, the students who are practicing seriously for the exams can go through the Go Math 4th Grade Key of Chapter 13 Perimeter and Area. You can test your knowledge by solving the problems in this HMH Go Math Grade 4 Answer Key Chapter Perimeter and Area.
Common Core – New – Page No. 721
Perimeter
Find the perimeter of the rectangle or square.
Question 1.
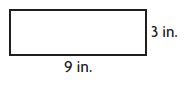
9+3+9+3=24
24 inches
Explanation:
Length = 9 inches
Width = 3 inches
Perimeter of the rectangle = l + w + l + w
9+3+9+3=24
Therefore the Perimeter of the rectangle = 24 inches.
Question 2.

_____ meters
Answer: 32 meters
Explanation:
Side of a square = 8 meters
The perimeter of a square = 4a
= 4 × 8 meters = 32 meters
Thus the perimeter of a square = 32 meters.
Question 3.
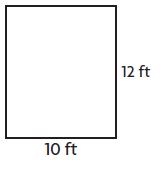
_____ feet
Answer: 44 feet
Explanation:
Length = 10 ft
Width = 12 ft
Perimeter of the rectangle = l + w + l + w
P = 10 + 12 + 10 + 12 = 20 + 24 = 44 feets
Thus the perimeter of the rectangle = 44 feet.
Remember: perimeter is the total distance around the outside, which can be found by adding together the length of each side. In the case of a rectangle, opposite sides are equal in length, so the perimeter is twice its width plus twice its height.
Question 4.
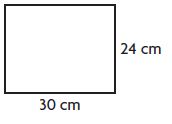
_____ centimeters
Answer: 108 centimeters
Explanation:
Length = 30 cm
Width = 24 cm
Perimeter of the rectangle = l + w + l + w
= 30 + 24 + 30 + 24 = 60 + 48
= 108 centimeters
Therefore the perimeter of the rectangle = 108 centimeters
Question 5.

_____ inches
Answer: 216 inches
Explanation:
Length = 25 in.
Width = 83 in.
Perimeter of the rectangle = l + w + l + w
= 25 + 83 + 25 + 83
= 216 inches
Thus the perimeter of the rectangle = 216 inches
Question 6.
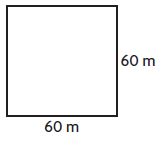
_____ meters
Answer: 240 meters
Explanation:
The side of a square = 60 meters
The perimeter of the square = 4a
= 4 × 60 meters = 240 meters
Thus the perimeter of the square = 240 meters.
Problem Solving
Question 7.
Troy is making a flag shaped like a square. Each side measures 12 inches. He wants to add ribbon along the edges. He has 36 inches of ribbon. Does he have enough ribbon? Explain.
_____
Answer: No. He needs 48 inches of ribbon.
Explanation:
Troy is making a flag shaped like a square. Each side measures 12 inches.
He wants to add a ribbon along the edges.
He has 36 inches of ribbon.
36 inches + 12 inches = 48 inches
Question 8.
The width of the Ochoa Community Pool is 20 feet. The length is twice as long as its width. What is the perimeter of the pool?
_____ feet
Answer: 120 feet
Explanation:
The width of the Ochoa Community Pool is 20 feet.
The length is twice as long as its width.
Length = 2 × 20 feet = 40 feet
Perimeter of the rectangle = l + w + l + w
= 40 + 20 + 40 + 20 = 120 feet
Thus the perimeter of the pool is 120 feet.
Common Core – New – Page No. 722
Lesson Check
Question 1.
What is the perimeter of a square window with sides 36 inches long?
Options:
a. 40 inches
b. 72 inches
c. 144 inches
d. 1,296 inches
Answer: 144 inches
Explanation:
Given, Side of a square = 36 inches
The perimeter of the square = 4 × side = 4a
= 4 × 36 inches = 144 inches
Thus the perimeter of the square = 144 inches
The correct answer is option C.
Question 2.
What is the perimeter of the rectangle below?
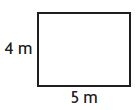
Options:
a. 11 meters
b. 14 meters
c. 18 meters
d. 400 meters
Answer: 18 meters
Explanation:
Length of the rectangle = 5 meter
Width of the rectangle = 4 meters
The perimeter of the rectangle = l + w + l + w
= 5 + 4 + 5 + 4 = 18 meters
Thus the correct answer is option C.
Spiral Review
Question 3.
Which is the most reasonable estimate for the measure of the angle Natalie drew?
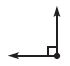
Options:
a. 30°
b. 90°
c. 180°
d. 210°
Answer: 90°
Explanation:
By seeing the above figure we can say that it is the right angle.
The correct answer is option B.
Question 4.
Ethan has 3 pounds of mixed nuts. How many ounces of mixed nuts does Ethan have?
Options:
a. 30 ounces
b. 36 ounces
c. 48 ounces
d. 54 ounces
Answer: 48 ounces
Explanation:
Given that, Ethan has 3 pounds of mixed nuts.
1 pound = 16 ounces
3 pounds = 3 × 16 ounces = 48 ounces
Therefore the correct answer is option C.
Question 5.
How many lines of symmetry does the shape below appear to have?
Options:
a. 0
b. 1
c. 2
d. more than 2
Answer: 1
Explanation:
The above shape has 1 line of symmetry.
The correct answer is option B.
Question 6.
Which of the following comparisons is correct?
Options:
a. 0.70 > 7.0
b. 0.7 = 0.70
c. 0.7 < 0.70
d. 0.70 = 0.07
Answer: 0.7 = 0.70
Explanation:
a. 0.70 > 7.0
7.0 = 7
0.7 is less than 7
b. 0.7 = 0.70
0.7 is nothing but 0.70
So, the comparision is correct.
The answer is option B.
Page No. 725
Question 1.
Find the area of the rectangle.
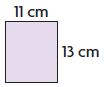
A = _____ square cm
Answer: 143 square cm
Explanation:
Length = 11 cm
Width = 13 cm
Area of the rectangle = l × w
= 11 cm × 13 cm = 143 square cm
Therefore the area of the rectangle = 143 square cm
Find the area of the rectangle or square.
Question 2.

A = _____ square inches
Answer: 14 square inches
Explanation:
Length = 7 inches
Width = 2 inches
Area of the rectangle = l × w
= 7 inches × 2 inches = 14 inches
Therefore the area of the rectangle = 14 square inches
Question 3.
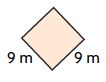
A = _____ square meters
Answer: 81 square meters
Explanation:
Side of the square = 9 m
Area of a square = s × s
= 9 m × 9 m = 81 square meters
Thus the area of a square = 81 square meters
Question 4.
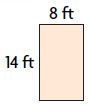
A = _____ square feet
Answer: 112 square feet
Explanation:
Length = 8 feet
Width = 14 feet
Area of the rectangle = l × w
= 8 feet × 14 feet = 112 square feet
Therefore, area of the rectangle = 112 square feet
Find the area of the rectangle or square.
Question 5.

A = _____ square feet
Answer: 65 square feet
Explanation:
Length of the rectangle = 13 ft
Width of the rectangle = 5 feet
Area of a rectangle = l × w
= 13 feet × 5 feet = 65 square feet
Thus, the area of the rectangle = 65 square feet
Question 6.
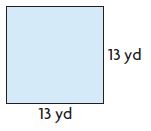
A = _____ square yards
Answer: 169 square yards
Explanation:
Side of the square = 13 yards
Area of a square = s × s
= 13 yards × 13 yards = 169 square yards
Therefore, the area of a square = 169 square yards
Question 7.
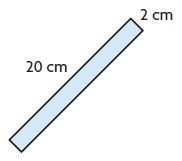
A = _____ square centimeters
Answer: 40 square centimeters
Explanation:
Length of the rectangle = 20 cm
Width of the rectangle = 2 cm
Area of a rectangle = l × w
= 20 cm × 2 cm = 40 square centimeters
Therefore the area of the rectangle = 40 square centimeters.
Practice: Copy and Solve Find the area of the rectangle.
Question 8.
base: 16 feet
height: 6 feet
A = _____ square feet
Answer: 96 square feet
Explanation:
base: 16 feet
height: 6 feet
Area of a rectangle = b ×h
= 16 feet × 6 feet = 96 square feet
Thus the area of the rectangle = 96 square feet
Question 9.
base: 9 yards
height: 17 yards
A = _____ square yards
Answer: 153 square yards
Explanation:
base: 9 yards
height: 17 yards
Area of a rectangle = b × h
9 yards × 17 yards = 153 square yards
The area of the rectangle = 153 square yards
Question 10.
base: 14 centimeters
height: 11 centimeters
A = _____ square centimeters
Answer: 154 square centimeters
Explanation:
base: 14 centimeters
height: 11 centimeters
Area of a rectangle = b × h
14 centimeters × 11 centimeters = 154 square centimeters
The area of the rectangle = 154 square centimeters
Question 11.
Terry’s rectangular yard is 15 meters by 18 meters. Todd’s rectangular yard is 20 meters by 9 meters. How much greater is the area of Terry’s yard than Todd’s yard?
_____ square meters
Answer: 90 square meters
Explanation:
Given,
Terry’s rectangular yard is 15 meters by 18 meters.
Todd’s rectangular yard is 20 meters by 9 meters.
Terry’s rectangular yard:
Area of a rectangle = b × h
= 15 meters × 18 meters = 270 square meters
Todd’s rectangular yard:
Area of a rectangle = b × h
20 meters × 9 meters = 180 square meters
270 square meters – 180 square meters = 90 square meters
Terry’s yard is 90 square meters greater than Todd’s yard.
Question 12.
Reason Quantitatively Carmen sewed a square baby quilt that measures 36 inches on each side. What is the area of the quilt?
A = _____ square inches
Answer: 1296 square inches
Explanation:
Carmen sewed a square baby quilt that measures 36 inches on each side.
Area of a square = s × s
= 36 inches × 36 inches = 1296 square inches
Therefore the area of the quilt is 1296 square inches.
Page No. 726

Question 13.
Nancy and Luke are drawing plans for rectangular flower gardens. In Nancy’s plan, the garden is 18 feet by 12 feet. In Luke’s plan, the garden is 15 feet by 15 feet. Who drew the garden plan with the greater area? What is the area?
a. What do you need to find?
Type below:
__________
Answer: I need to find who drew the garden plan with the greater area.
Question 13.
b. What formula will you use?
Type below:
__________
Answer: I will Area of rectangle and Area of a square formula
Question 13.
c. What units will you use to write the answer?
Type below:
__________
Answer: Square feet units
Question 13.
d. Show the steps to solve the problem.
Type below:
__________
Answer:
First, we need to find the area of Nancy’s plan
Length = 18 feet
Width = 12 feet
Area of a rectangle = l × w
A = 18 feet × 12 feet = 216 square feet
And now we need to find the area of Luke’s plan
A = s × s
A = 15 feet × 15 feet = 225 square feet
Question 13.
e. Complete the sentences.
The area of Nancy’s garden is _______.
The area of Luke’s garden is _______.
_______ garden has the greater area.
Type below:
__________
Answer:
The area of Nancy’s garden is 216 square feet.
The area of Luke’s garden is 225 square feet.
Luke’s garden has a greater area.
Question 14.
Victor wants to buy fertilizer for his yard. The yard is 35 feet by 55 feet. The directions on the bag of fertilizer say that one bag will cover 1,250 square feet. How many bags of fertilizer should Victor buy to be sure that he covers the entire yard?
______ bags
Answer: 2 bags
Explanation:
Given that,
Victor wants to buy fertilizer for his yard. The yard is 35 feet by 55 feet.
The directions on the bag of fertilizer say that one bag will cover 1,250 square feet.
A = b × h
A = 35 feet × 55 feet
A = 1925 square feet
1925 square feet is greater than 1,250 square feet.
So, Victor has to buy 2 bags to be sure that he covers the entire yard.
Question 15.
Tuan is an artist. He is painting on a large canvas that is 45 inches wide. The height of the canvas is 9 inches less than the width. What is the area of Tuan’s canvas?
A = ______ square inches
Answer: 1620 square inches
Explanation:
Tuan is an artist. He is painting on a large canvas that is 45 inches wide.
The height of the canvas is 9 inches less than the width.
So, h = 45 – 9 = 36 inches
A = b × h
A = 45 inches × 36 inches
A = 1,620 square inches
Therefore the area of Tuan’s canvas is 1620 square inches.
Common Core – New – Page No. 727
Area
Find the area of the rectangle or square.
Question 1.
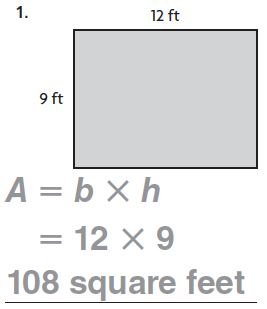
Question 2.

______ square yards
Answer: 64 square yards
Explanation:
Side of the square = 8 yards
Area of the square = s × s
8 yards × 8 yards = 64 square yards
Therefore, The area of the square is 64 square yards.
Question 3.
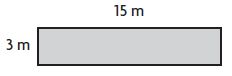
_____ square meters
Answer: 45 square meters
Explanation:
Length of the rectangle = 15 m
Width of the rectangle = 3 m
Area of the rectangle = b × h
= 15 m × 3 m = 45 square meters
Thus the area of the rectangle is 45 square meters.
Question 4.
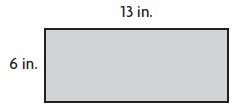
______ square inches
Answer: 78 square inches
Explanation:
The base of the rectangle = 13 in.
Height of the rectangle = 6 in.
Area of the rectangle = b × h
13 in. × 6 in. = 78 square inches
Thus the area of the rectangle is 78 square inches.
Question 5.
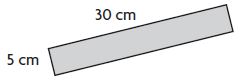
______ square centimeters
Answer: 150 square centimeters
Explanation:
The base of the rectangle = 30 cm
Height of the rectangle = 5 cm
Area of the rectangle = b × h
30 cm × 5 cm = 150 square centimeters
Therefore, the area of the rectangle = 150 square centimeters
Question 6.
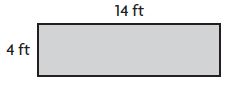
______ square feet
Answer: 56 square feet
Explanation:
The base of the rectangle = 14 feet
Height of the rectangle = 4 feet
Area of the rectangle = b × h
14 feet × 4 feet = 56 square feet
Therefore, the area of the rectangle = 56 square feet.
Problem Solving
Question 7.
Meghan is putting wallpaper on a wall that measures 8 feet by 12 feet. How much wallpaper does Meghan need to cover the wall?
______ square feet wallpaper
Answer: 96 square feet
Explanation:
Meghan is putting wallpaper on a wall that measures 8 feet by 12 feet.
The base of the rectangle = 8 feet
Height of the rectangle = 12 feet
Area of the rectangle = b × h
8 feet × 12 feet = 96 square feet
Thus the Area of the rectangle = 96 square feet
Question 8.
Bryson is laying down sod in his yard to grow a new lawn. Each piece of sod is a 1-foot by 1-foot square. How many pieces of sod will Bryson need to cover his yard if his yard measures 30 feet by 14 feet?
______ pieces
Answer: 420 pieces
Explanation:
Bryson is laying down sod in his yard to grow a new lawn.
Each piece of sod is a 1-foot by 1-foot square.
The base of the rectangle = 30 feet
Height of the rectangle = 14 feet
Area of the rectangle = b × h
= 30 feet × 14 feet = 420 sq. ft.
Therefore Bryson needs 420 pieces of sod to cover his yard.
Common Core – New – Page No. 728
Lesson Check
Question 1.
Ellie and Heather drew floor models of their living rooms. Ellie’s model represented 20 feet by 15 feet. Heather’s model represented 18 feet by 18 feet. Whose floor model represents the greater area? How much greater?
Options:
a. Ellie; 138 square feet
b. Heather; 24 square feet
c. Ellie; 300 square feet
d. Heather; 324 square feet
Answer: Heather; 24 square feet
Explanation:
Given,
Ellie and Heather drew floor models of their living rooms.
Ellie’s model represented 20 feet by 15 feet.
Heather’s model represented 18 feet by 18 feet.
Area of Ellie’s model = 20 feet × 15 feet = 300 square feet
Area of Heather’s model = 18 feet × 18 feet = 324 square feet
Now subtract the area of Ellie’s model from Heather’s model = 324 square feet – 300 square feet = 24 square feet
Thus the area of Heather’s model is greater than Ellie’s model
The correct answer is option B.
Question 2.
Tyra is laying down square carpet pieces in her photography studio. Each square carpet piece is 1 yard by 1 yard. If Tyra’s photography studio is 7 yards long and 4 yards wide, how many pieces of square carpet will Tyra need?
Options:
a. 10
b. 11
c. 22
d. 28
Answer: 28
Explanation:
Tyra is laying down square carpet pieces in her photography studio.
Each square carpet piece is 1 yard by 1 yard. Tyra’s photography studio is 7 yards long and 4 yards wide
Area of the rectangle = b × h
= 7 yards × 4 yards
= 28 square yards
Thus the correct answer is option D.
Spiral Review
Question 3.
Typically, blood fully circulates through the human body 8 times each minute. How many times does blood circulate through the body in 1 hour?
Options:
a. 48
b. 240
c. 480
d. 4,800
Answer: 480
Explanation:
Blood fully circulates through the human body 8 times each minute.
1 minute = 60 seconds
8 × 60 seconds = 480 seconds
The correct answer is option C.
Question 4.
Each of the 28 students in Romi’s class raised at least $25 during the jump-a-thon. What is the least amount of money the class raised?
Options:
a. $5,200
b. $700
c. $660
d. $196
Answer: $700
Explanation:
Each of the 28 students in Romi’s class raised at least $25 during the jump-a-thon.
Multiply number od students with $25
28 × $25 = $700
The correct answer is option B.
Question 5.
What is the perimeter of the shape below if 1 square is equal to 1 square foot?

Options:
a. 12 feet
b. 14 feet
c. 24 feet
d. 28 feet
Answer: 28 feet
Explanation:
Given that 1 square is equal to 1 square foot
There are 14 squares
Length = 14 squares
Width = 2 squares
Area of the rectangle = l × w = 14 × 2 = 28 sq. feets
The correct answer is option D.
Question 6.
Ryan is making small meat loaves. Each small meat loaf uses \(\frac{3}{4}\) pound of meat. How much meat does Ryan need to make 8 small meat loaves?
Options:
a. 4 pounds
b. 6 pounds
c. 8 pounds
d. 10 \(\frac{2}{3}\) pounds
Answer: 6 pounds
Explanation:
Ryan is making small meatloaves.
Each small meatloaf uses \(\frac{3}{4}\) pound of meat.
Ryan need to make 8 small meatloaves.
\(\frac{3}{4}\) × 8 = 6 pounds
The correct answer is option B.
Page No. 731
Question 1.
Explain how to find the total area of the figure.
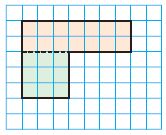
A = ______ square units
Answer: 23 square units
Explanation:
Rectangle:
Each square box = 1 unit
There are 7 units
Base = 7 units
Height = 2 units
The area of the figure = b × h
A = 7 units × 2 units = 14 square units
Square:
The side is 3 units
Area of the square = 3 units × 3 units = 9 square units
Add both the areas = 14 square units + 9 square units = 23 square units
Therefore the area of the above figure is 23 square units.
Find the area of the combined rectangles.
Question 2.
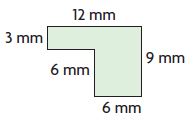
A = ______ square mm
Answer: 72 square mm
Explanation:
Area of top rectangle = b × h
Base = 12 mm
Height = 3 mm
A = 12 mm × 3 mm = 36 square mm
Area of square = s × s
s = 6 mm
A = 6 mm × 6 mm = 36 square mm
Area of the figure = 36 square mm + 36 square mm = 72 square mm
Thus the area of the above figure is 72 square mm.
Question 3.
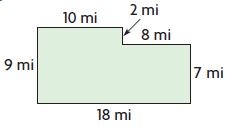
A = ______ square miles
Answer: 146 square miles
Explanation:
Area of rectangle = b × h
Area of the first rectangle = 10 mi × 9 mi
A = 90 square miles
Area of the second rectangle = 8 mi × 7 mi
A = 56 square miles
Area of the figure = Area of first rectangle + Area of the second rectangle
Area of the figure = 90 square mi + 56 square miles
Thus the Area of the figure = 146 square miles
Question 4.
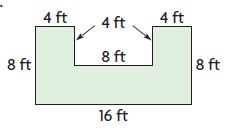
A = ______ square feet
Answer: 96 square feet
Explanation:
There are 2 squares and one rectangle in this figure
Area of the square = s × s
A = 4 ft × 4 ft = 16 square ft
Area of the square = s × s
A = 4 ft × 4 ft = 16 square ft
Area of the rectangle = b × h
A = 16 ft × 4 ft = 64 square ft
Area of the figure = 16 square ft + 16 square ft + 64 square ft
Thus the Area of the figure = 96 square feet.
Find the area of the combined rectangles.
Question 5.
Attend to Precision Jamie’s mom wants to enlarge her rectangular garden by adding a new rectangular section. The garden is now 96 square yards. What will the total area of the garden be after she adds the new section?
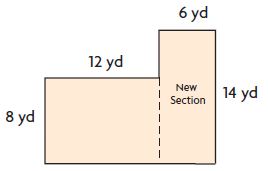
A = ______ square yards
Answer: 180 square yards
Explanation:
There are 2 rectangles in the above figure
Area of rectangle = b × h
A = 12 yard × 8 yards = 96 square yards
Area of rectangle = b × h
A = 6 yards × 14 yards = 84 square yards
Area of the figure = 96 square yards + 84 square yards
Therefore the area of the figure = 180 square yards.
Question 6.
Explain how to find the perimeter and area of the combined rectangles at the right.
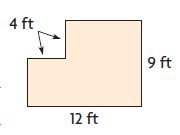
P = ______ feet; A = ______ square feet
Answer: A = 92 square feet; P = 52 feet
Explanation:
There are 2 rectangle in the figure
Area of rectangle = b × h
A = 5 ft × 4 ft = 20 square ft
Area of rectangle = b × h
A = 8 ft × 9 ft = 72 square ft
Area of the figure = 20 square ft + 72 square ft = 92 square ft
Perimeter of the rectangle = 2l + 2w
P = 2 × 5 + 2 × 4 = 10 + 8 = 18 feet
Perimeter of the rectangle = 2l + 2w
P = 2 × 8 + 2 × 9 = 16 + 18 = 34 feet
Perimeter of the figure = 52 feet
Page No. 732

Question 7.
The diagram shows the layout of Mandy’s garden. The garden is the shape of combined rectangles. What is the area of the garden?
a. What do you need to find?
Type below:
__________
Answer: I need to find the area of the garden.
Question 7.
b. How can you divide the figure to help you find the total area?
Type below:
__________
Answer: I will divide the figure into 3 parts to find the total area
Question 7.
c. What operations will you use to find the answer?
Type below:
__________
Answer: I will use the addition operation to find the area.
Question 7.
d. Draw a diagram to show how you divided the figure. Then show the steps to solve the problem.
Type below:
__________
Answer:
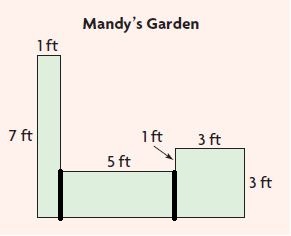
There are 2 rectangles and 1 square in this figure.
Area of rectangle = b × h
Base = 1 ft
H = 7 ft
A = 1 ft × 7 ft = 7 square ft
Area of rectangle = b × h
Base = 5 ft
H = 2 ft
A = 5 ft × 2 ft = 10 square ft
Area of the square = s × s
A = 3 ft × 3 ft = 9 square ft
Total area = 7 square ft + 10 square ft + 9 square ft
= 26 square ft
Question 8.
Workers are painting a large letter L for an outdoor sign. The diagram shows the dimensions of the L. For numbers 8a–8c, select Yes or No to tell whether you can add the products to find the area that the workers will paint.

8a. 2 × 8 and 2 × 4
i. yes
ii. no
Answer: Yes
Explanation:
There are 2 rectangles in the above figure
B = 2 ft
H = 8 ft
A = 2 × 8
B = 4 ft
H = 2 ft
A = 4 × 2
Thus the above statement is correct.
Question 8.
8b. 2 × 6 and 2 × 8
i. yes
ii. no
Answer: No
There are 2 rectangles in the above figure
B = 6 ft
H = 2 ft
A = 2 × 6
Then 2 will be subtracted from 8 = 6
So, the above statement 2 × 6 and 2 × 8 is false.
Question 8.
8c. 2 × 6 and 6 × 2
i. yes
ii. no
Answer: Yes
Explanation:
There are 2 rectangles in the above figure
B = 6 ft
H = 2 ft
A = 6 × 2
B = 2 ft
H = 6 ft
A = 2 × 6
Thus the above statement is true.
Common Core – New – Page No. 733
Area of Combined Rectangles
Find the area of the combined rectangles.
Question 1.

Question 2.

______ square feet
Answer: 143 square feet
Explanation:
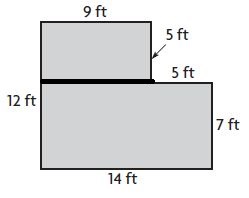
Area of A = 9 ft × 5 ft = 45 sq. ft.
Area of B = 14 ft. × 7 ft. = 98 sq. ft.
Total Area = Area of A + Area of B
= 45 sq. ft. + 98 sq. ft. = 143 square feet
Therefore the total Area = 143 square feet
Question 3.
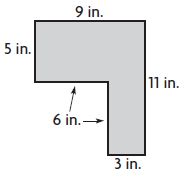
______ square inches
Answer: 63 square inches
Explanation:

Area of A = 9 in. × 5 in. = 45 square inches
Area of B = 6 inches × 3 inches = 18 square inches
Total Area = Area of A + Area of B
Total Area = 45 square inches + 18 square inches
Total Area = 63 square inches
Question 4.
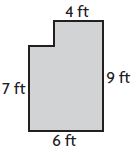
______ square feet
Answer: 50 square feet
Explanation:
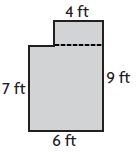
Area of A = 4 feet × 2 feet = 8 square feet
Area of B = 7 feet × 6 feet = 42 square feet
Total Area = Area of A + Area of B
Total Area = 8 square feet + 42 square feet
Total Area = 50 square feet
Question 5.
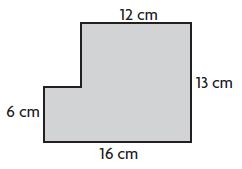
______ square centimeters
Answer: 180 square centimeters
Explanation:
Area of A = 12 cm × 7 cm = 84 square cm
Area of B = 16 cm × 6 cm = 96 square cm
Total Area = Area of A + Area of B
Total Area = 84 square cm + 96 square cm
Total Area = 180 square centimeters
Question 6.
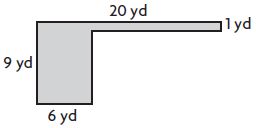
______ square yards
Answer: 68 square yards
Explanation:
Area of A = 14 yd × 1 yd = 14 square yards
Area of B = 9 yd × 6 yd = 54 square yards
Total Area = Area of A + Area of B
Total Area = 14 square yards + 54 square yards
Total Area = 68 square yards
Problem Solving
Use the diagram for 7–8.
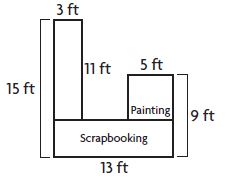
Nadia makes the diagram below to represent the counter space she wants to build in her craft room.
Question 7.
What is the area of the space that Nadia has shown for scrapbooking?
______ square feet
Answer: 52 square feet
Explanation:
Length = 13 feet
Width = 9 feet – 5 feet = 4 feet
Area of scrapbooking = l × w
= 13 feet × 4 feet
= 52 square feet
Therefore the area of the space that Nadia has shown for scrapbooking is 52 square feet.
Question 8.
What is the area of the space she has shown for painting?
______ square feet
Answer: 25 square feet
Explanation:
The space for painting is a square.
Side of the square is 5 feet
Area of the square = 5 feet × 5 feet
= 25 square feet
Thus the area of the space she has shown for painting is 25 square feet.
Common Core – New – Page No. 734
Lesson Check
Question 1.
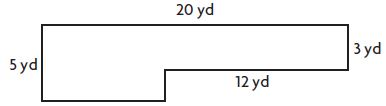
What is the area of the combined rectangles below?
Options:
a. 136 square yards
b. 100 square yards
c. 76 square yards
d. 64 square yards
Answer: 76 square yards
Explanation:
Area of 1st rectangle = 5 yards × 8 yards = 40 square yards
Area of 2nd rectangle = 12 yards × 3 yards = 36 square yards
Area of the figure = Area of 1st rectangle + Area of 2nd rectangle
Area of the figure = 40 square yards + 36 square yards
Therefore, the Area of the figure is 76 square yards.
So, the correct answer is option C.
Question 2.
Marquis is redecorating his bedroom. What could Marquis use the area formula to find?
Options:
a. how much space should be in a storage box
b. what length of wood is needed for a shelf
c. the amount of paint needed to cover a wall
d. how much water will fill up his new aquarium
Answer: the amount of paint needed to cover a wall
Spiral Review
Question 3.
Giraffes are the tallest land animals. A male giraffe can grow as tall as 6 yards. How tall would the giraffe be in feet?
Options:
a. 2 feet
b. 6 feet
c. 12 feet
d. 18 feet
Answer: 18 feet
Explanation:
Giraffes are the tallest land animals. A male giraffe can grow as tall as 6 yards.
6 yards + 6 yards + 6 yards = 18 yards
The correct answer is option D.
Question 4.
Drew purchased 3 books for $24. The cost of each book was a multiple of 4. Which of the following could be the prices of the 3 books?
Options:
a. $4, $10, $10
b. $4, $8, $12
c. $5, $8, $11
d. $3, $7, $14
Answer: $4, $8, $12
Explanation:
Given that,
Drew purchased 3 books for $24.
The cost of each book was a multiple of 4.
So, the prices of books will be multiple of 4.
That means $4 × 1, $4 × 2, $4 × 3
= $4, $8, $12
The correct answer is option B.
Question 5.
Esmeralda has a magnet in the shape of a square. Each side of the magnet is 3 inches long. What is the perimeter of her magnet?
Options:
a. 3 inches
b. 7 inches
c. 9 inches
d. 12 inches
Answer: 12 inches
Explanation:
Esmeralda has a magnet in the shape of a square. Each side of the magnet is 3 inches long.
Side = 3 inches
The perimeter of the square = 4s
P = 4 × 3 = 12 inches
The correct answer is option D.
Question 6.
What is the area of the rectangle below?

Options:
a. 63 square feet
b. 32 square feet
c. 18 square feet
d. 16 square feet
Answer: 63 square feet
Explanation:
Area of the rectangle = base × height
Base = 9 feet
Height = 7 feet
A = 9 feet × 7 feet
A = 63 square feet
Thus the correct answer is option A.
Page No. 735
Choose the best term from the box.

Question 1.
A square that is 1 unit wide and 1 unit long is a ________.
__________
Answer: Square unit
Question 2.
The _______ of a two-dimensional figure can be any side.
__________
Answer: Base
Question 3.
A set of symbols that expresses a mathematical rule is called a ______.
__________
Answer: Formula
Question 4.
The ______ is the distance around a shape.
__________
Answer: Perimeter
Find the perimeter and area of the rectangle or square.
Question 5.
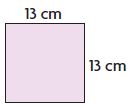
Perimeter = ______ cm
Area = ______ square cm
Answer:
Perimeter = 52 cm
Area = 169 square cm
Explanation:
P = 4s
P = 4 × 13 = 52 cm
A = s × s
A = 13 × 13 = 169 square cm
Question 6.

Perimeter = ______ ft
Area = ______ square ft
Answer:
Perimeter: 48 ft
Area = 63 square ft
Explanation:
Base = 21 ft
Height = 3 ft
P = 2l +2w
P = 2 (21 ft + 3 ft)
P = 2 × 24 = 48 feet
A = b × h
A = 21 × 3
A = 63 square ft
Question 7.
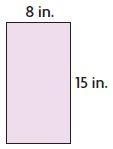
Perimeter = ______ in.
Area = ______ square in.
Answer:
Perimeter = 46 in.
Area = 120 square in.
Explanation:
P = 2l +2w
P = 2 × 15 + 2 × 8
P = 30 + 16 = 46 inches
A = l × w
A = 15 × 8 = 120 square inches
Question 8.
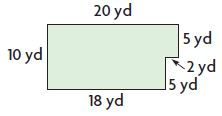
Area = ____ square yd
Answer:
Area of the rectangle = 20 yards × 5 yards = 100 square yards
Area of the rectangle = 18 yards × 5 yards = 90 square yards
Area of the figure = 100 square yards + 90 square yards = 190 square yards
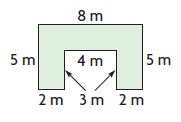
Question 9.
Area = ____ square meters
Answer:
A = b × h
A = 5 m × 2 m = 10 square meters
A = b × h
A = 5 m × 2 m = 10 square meters
A = b × h
A = 4 m × 2 m = 8 square meters
Now add all the areas
10 square meters + 10 square meters + 8 square meters
= 28 square meters
Therefore the area of the figures is 28 square meters
Question 10.

Area = ____ square feet
Answer:
Area of the rectangle = b × h
A = 14 ft × 2 ft = 28 square feet
A = s × s
A = 8 ft × 8 ft = 64 square feet
Area of the figures = 64 square feet + 28 square feet
Therefore Area of the figure = 92 square feet
Page No. 736
Question 11.
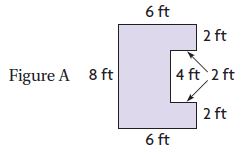
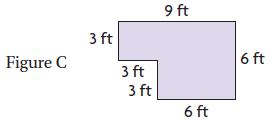
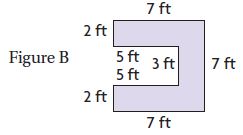
Which figure has the greatest perimeter?
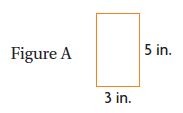
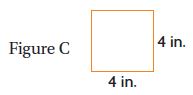


________
Answer: Figure B has the highest perimeter.
Explanation:

P = 2l +2w
P = 2 × 3 + 2 ×5 = 6 + 10 = 16

P = 2 × 6 + 2 × 3 = 12 + 6 = 18
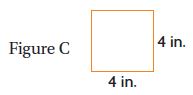
P = 4a = 4 × 4 = 16

P = 2 × 4 + 2 × 3 = 8+ 6 = 14
Thus the greatest perimeter is figure B.
Question 12.
Which figure has an area of 108 square centimeters?
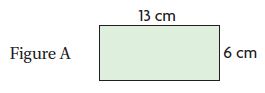
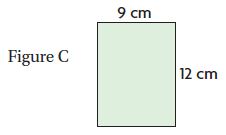
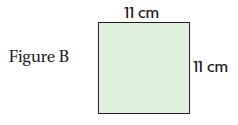
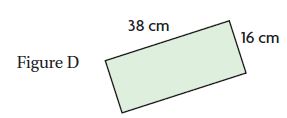
________
Answer: Figure C
Explanation:

A = 13 cm × 6 cm = 78 square cm.

A = 11 cm × 11 cm = 121 square cm.

A = 12 cm × 9 cm = 108 square cm.

A = 16 cm × 38 cm = 608 square cm.
Thus the area of 108 square centimeters is Figure C.
Question 13.
Which of the combined rectangles has an area of 40 square feet?
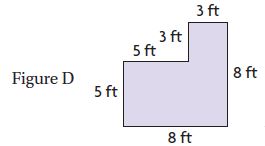
________
Answer: Figure A
Explanation:

Area of top rectangle = 6 ft × 2 ft = 12 square feet
Area of bottom rectangle = 6 ft × 2 ft = 12 square feet
Area of square = 4 ft × 4 ft = 16 square feet
Add Area of top rectangle, Area of bottom rectangle and Area of square
= 12 square feet + 12 square feet + 16 square feet = 40 square feet.
Thus the correct answer is option A.
Page No. 739
Question 1.
Find the unknown measure. The area of the rectangle is 36 square feet.
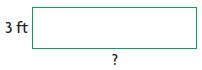
A = b × h
The base of the rectangle is ________ .
base = _____ ft
Answer: 12 feet
Explanation:
Given,
The area of the rectangle = 36 square feet
Height = 3 feet
Base =?
A = b × h
36 square feet = b × 3 feet
b × 3 feet = 36 square feet
b = 36/3 = 12 feet
The base of the rectangle is 12 feets.
Find the unknown measure of the rectangle.
Question 2.
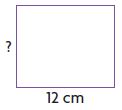
Perimeter = 44 centimeters
width = _____ cm
Answer: 10 cm
Explanation:
Given,
Perimeter = 44 centimeters
Length = 12 cm
width =?
The perimeter of the rectangle = 2 (l + w)
P = 2l + 2w
44 cm = 24 cm + 2w
2w = 44 cm – 24 cm
2w = 20 cm
w = 20/2 = 10
Therefore width = 10 cm
Question 3.
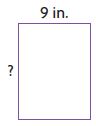
Area = 108 square inches
height = _____ in.
Answer: 12 inches
Explanation:
Given,
Area = 108 square inches
Base = 9 inches
height = _____ in.
A = b × h
108 square inches = 9 inches × h
h = 108/9
Height = 12 inches
Therefore the height of the rectangle = 12 inches
Question 4.

Area = 90 square meters
base = _____ cm
Answer: 18 meters
Explanation:
Given,
Area = 90 square meters
Height = 5 meters
base = _____ cm
A = b × h
90 square meters = b × 5 meters
b × 5 meters = 90 square meters
b = 90/5 = 18 meters
Therefore the base of the rectangle = 18 meters
Question 5.

Perimeter = 34 yards
length = _____ yd
Answer: 12 yards
Explanation:
Given,
Perimeter = 34 yards
Width = 5 yards
Length =?
The perimeter of the rectangle = 2 (l + w)
P = 2l + 2w
34 yards = 2 × l + 2 × 5 yards
34 yards = 2 × l + 10 yards
2 × l + 10 yards = 34 yards
2l = 34 yards – 10 yards
2l = 24 yards
l = 24/2 = 12 yards
Therefore the length of the rectangle = 12 yards.
Question 6.

Area = 96 square feet
base = ______ ft
Answer: 12 feet
Explanation:
Given,
Area = 96 square feet
Height = 8 feet
Base =?
A = b × h
96 square feet = b × 8 feet
b × 8 feet = 96 square feet
b = 96/8 = 12 feet
Thus base of the rectangle = 12 feet.
Question 7.

Area = 126 square centimeters
height = _____ centimeters
Answer: 14 centimeters
Explanation:
Given,
Area = 126 square centimeters
Base = 9 cm
height = _____ centimeters
A = b × h
126 square centimeters = 9 cm × h
9 cm × h = 126 square centimeters
h = 126/9 = 14 centimeters
Therefore the Height of the rectangle = 14 centimeters
Question 8.
A square has an area of 49 square inches. Explain how to find the perimeter of the square.
Type below:
________
Answer:
Explanation:
Given that,
A square has an area of 49 square inches.
A = 49 square inches
s^2 = 49 square inches
The square root of 49 is 7
So, each side of the square is 7 inches
The perimeter of the square = 4 × s
4 × 7 inches = 28 inches.
Therefore the perimeter of the square is 28 inches.
Page No. 740
Question 9.
Identify Relationships The area of a swimming pool is 120 square meters. The width of the pool is 8 meters. What is the length of the pool in centimeters?
length = _____ centimeters
Answer:
Given that the area of a swimming pool is 120 square meters.
The width of the pool is 8 meters.
We have to find the length of the pool in centimeters.
We know that Area of the rectangle = l × w
A = l × w
120 square meters = l × 8 meters
l × 8 meters = 120 square meters
l = 120/8 = 15 meters
Therefore, the length of the pool = 15 meters
Convert meters to centimeters
1 meter = 100 centimeters
15 meters = 1500 centimeters.
The length of the pool in centimeters = 1500 centimeters
Question 10.
An outdoor deck is 7 feet wide. The perimeter of the deck is 64 feet. What is the length of the deck? Use the numbers to write an equation and solve. A number may be used more than once.
![]()
P=(2 × l) + (2 × w)
So, the length of the deck is _______ feet.
length = _____ ft
Answer:
An outdoor deck is 7 feet wide.
The perimeter of the deck is 64 feet.
We know that,
P=(2 × l) + (2 × w)
64 feet = (2 × l) + (2 × 7)
64 feet = 2l + 14 feet
2 × l = 64 feet – 14 feet
2 × l = 50 feet
l = 50/2 = 25 feet
Therefore the length of the deck = 25 feet.
Question 11.
A male mountain lion has a rectangular territory with an area of 96 square miles. If his territory is 8 miles wide, what is the length of his territory?

length = _____ miles
Answer:
A male mountain lion has a rectangular territory with an area of 96 square miles.
Width = 8 miles
Length =?
A = l × w
96 square miles = l × 8 miles
l × 8 miles = 96 square miles
l = 96/8
l = 12 miles
Therefore, length of his territory = 12 miles
Common Core – New – Page No. 741
Find Unknown Measures
Find the unknown measure of the rectangle.
Question 1.
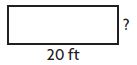
Perimeter = 54 feet
width = 7 feet
Think: P = (2 × l) + (2 × w)
54 = (2 × 20) + (2 × w)
54 = 40 + (2 × w)
Since 54 = 40 + 14, 2 × w = 14, and w = 7.
Question 2.
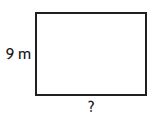
Perimeter = 42 meters
length = _____ meters
Answer: length = 12 meters
Explanation:
Given, Perimeter = 42 meters
Width = 9 meters
P = (2 × l) + (2 × w)
P = (2 × l) + (2 × 9 m)
42 m = 2l + 18 m
42 m – 18 m = 2l
2l = 24 meters
l = 24 meters/2 = 12 meters
Therefore length = 12 meters
Question 3.

Area = 28 square centimeters
height = _____ centimeters
Answer: height = 7 centimeters
Explanation:
Given,
Area = 28 square centimeters
Base = 4 cm
A = b × h
28 square centimeters = 4 cm × h
4 × h = 28
h = 28/4 = 7 cm
The height of the rectangle = 7 centimeters
Question 4.

Area = 200 square inches
base = _____ inches
Answer: base = 8 inches
Explanation:
Given,
Area = 200 square inches
Height = 25 inches
Base = ?
Area of the rectangle = b × h
200 square inches = b × 25 inches
b × 25 inches = 200 square inches
b = 200/25 = 8 inches
The base of the rectangle = 8 inches.
Problem Solving
Question 5.
Susie is an organic vegetable grower. The perimeter of her rectangular vegetable garden is 72 yards. The width of the vegetable garden is 9 yards. How long is the vegetable garden?
length = _____ yards
Answer: 27 yards
Explanation:
Susie is an organic vegetable grower.
The perimeter of her rectangular vegetable garden is 72 yards.
The width of the vegetable garden is 9 yards.
P = 72 yards
W = 9 yards
L =?
We know that,
P = (2 × l) + (2 × w)
72 yards = (2 × l) + (2 × 9)
72 yards – 18 yards = (2 × l)
(2 × l) = 72 yards – 18 yards
2l = 54 yards
l = 54/2 = 27 yards
Thus the vegetable garden is 27 yards long.
Question 6.
An artist is creating a rectangular mural for the Northfield Community Center. The mural is 7 feet tall and has an area of 84 square feet. What is the length of
the mural?
length = _____ feet
Answer: 12 feet
Explanation:
An artist is creating a rectangular mural for the Northfield Community Center.
The mural is 7 feet tall and has an area of 84 square feet.
A = 84 square feet
W = 7 feet
L =?
A = l × w
84 square feet = l × 7 feet
l × 7 feet = 84 square feet
l = 84/7 = 12 feet
Thus the length of Murali is 12 feet.
Common Core – New – Page No. 742
Lesson Check
Question 1.
The area of a rectangular photograph is 35 square inches. If the width of the photo is 5 inches, how tall is the photo?
Options:
a. 5 inches
b. 7 inches
c. 25 inches
d. 30 inches
Answer: 7 inches
Explanation:
The area of a rectangular photograph is 35 square inches.
Width = 5 inches
A = l × w
35 square inches = l × 5 inches
Length = 35/5 = inches
Thus the photo is 7 inches tall.
The correct answer is option B.
Question 2.
Natalie used 112 inches of blue yarn as a border around her rectangular bulletin board. If the bulletin board is 36 inches wide, how long is it?
Options:
a. 20 inches
b. 38 inches
c. 40 inches
d. 76 inches
Answer: 20 inches
Explanation:
Natalie used 112 inches of blue yarn as a border around her rectangular bulletin board.
Width = 36 inches
A = 112 inches
A = l × w
112 inches = l × 36 inches
l × 36 inches = 112 inches
l = 112/36 = 20 inches
Length = 20 inches
The correct answer is option A.
Spiral Review
Question 3.
A professional basketball court is in the shape of a rectangle. It is 50 feet wide and 94 feet long. A player ran one time around the edge of the court. How far did the player run?
Options:
a. 144 feet
b. 194 feet
c. 238 feet
d. 288 feet
Answer: 288 feet
Explanation:
A professional basketball court is in the shape of a rectangle.
It is 50 feet wide and 94 feet long.
A player ran one time around the edge of the court.
P = (2 × l) + (2 × w)
P = (2 × 94 feet) + (2 × 50 feet)
P = 188 feet + 100 feet = 288 feet
Therefore the perimeter of the rectangle is 288 feet.
Question 4.
On a compass, due east is a \(\frac{1}{4}\) turn clockwise from due north. How many degrees are in a \(\frac{1}{4}\) turn?
Options:
a. 45°
b. 60°
c. 90°
d. 180°
Answer: 90°
Explanation:
On a compass, due east is a \(\frac{1}{4}\) turn clockwise from due north.
\(\frac{1}{4}\) × 360° = 360°/4 = 90°
The correct answer is option C.
Question 5.
Hakeem’s frog made three quick jumps. The first was 1 meter. The second jump was 85 centimeters. The third jump was 400 millimeters. What was the total length of the frog’s three jumps?
Options:
a. 189 centimeters
b. 225 centimeters
c. 486 centimeters
d. 585 millimeters
Answer: 225 centimeters
Explanation:
Hakeem’s frog made three quick jumps.
The first was 1 meter. The second jump was 85 centimeters. The third jump was 400 millimeters.
Convert other units to centimeters
1 meter = 100 centimeters
400 millimeters = 40 centimeters
100 + 85 + 40 = 225 centimeters
Thus the correct answer is option B.
Question 6.
Karen colors in squares on a grid. She colored \(\frac{1}{8}\) of the squares blue and \(\frac{5}{8}\) of the squares red. What fraction of the squares are not colored in?
Options:
a. \(\frac{1}{8}\)
b. \(\frac{1}{4}\)
c. \(\frac{1}{2}\)
d. \(\frac{3}{4}\)
Answer: \(\frac{1}{4}\)
Explanation:
Karen colors in squares on a grid.
She colored \(\frac{1}{8}\) of the squares blue and \(\frac{5}{8}\) of the squares red.
\(\frac{1}{8}\) + \(\frac{5}{8}\) = \(\frac{6}{8}\)
Total number of fractions = \(\frac{8}{8}\)
\(\frac{8}{8}\) – \(\frac{6}{8}\) = \(\frac{2}{8}\)
\(\frac{1}{4}\) fraction of the squares are not colored.
Page No. 745
Question 1.
Lila is wallpapering one wall of her bedroom, as shown in the diagram. She will cover the whole wall except for the doorway. How many square feet of wall does Lila need to cover?
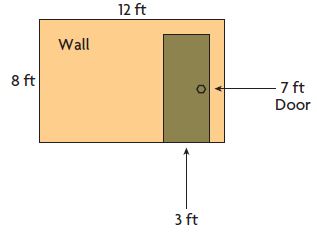
First, find the area of the wall.
A = b × h
Awall = _____ square feet
Answer:
Base = 12 feet
Height = 8 feet
A = b × h
Awall = 12 feet × 8 feet
Awall = 96 square feet
Question 1.
Next, find the area of the door.
A = b × h
Adoor = _____ square feet
Answer:
Base = 3 feet
Height = 7 feet
A = b × h
Adoor = 3 feet × 7 feet
Adoor = 21 square feet
Question 1.
Last, subtract the area of the door from the area of the wall.
_____ – _____ = _____ square feet
So, Lila needs to cover _____ of wall.
Type below:
________
Answer:
Adoor = 21 square feet
Awall = 96 square feet
Last, subtract the area of the door from the area of the wall.
A = Awall – Adoor
A = 96 square feet – 21 square feet
A = 75 square feet
So, Lila needs to cover 75 square feet
Question 2.
What if there was a square window on the wall with a side length of 2 feet? How much wall would Lila need to cover then? Explain.
______ square feet
Answer:
If there is a square window of length 2 feet
Area of square = s × s
Awindow = 2 × 2 = 4 square feet
Now Subtract the area of the door, area of the window from the area of the wall.
A = 96 square feet – 21 square feet – 4 square feet
A = 71 square feet
Therefore Lila need to cover 71 square feet.
Question 3.
Ed is building a model of a house with a flat roof, as shown in the diagram. There is a chimney through the roof. Ed will cover the roof with square tiles. If the area of each tile is 1 square inch, how many tiles will he need? Explain.
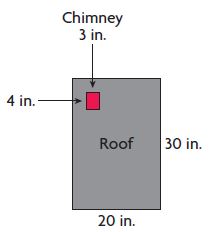
_____ tiles
Answer:
Roof:
Base = 20 inches
Height = 30 inches
Area of the roof = b × h
Aroof = 20 inches × 30 inches
Aroof = 600 inches
Chimney:
Base = 3 inches
Height = 4 inches
Area of the chimney = b × h
Achimney = 3 × 4 = 12 inches
Now subtract Area of Chimney from Area of the roof
A = 600 inches – 12 inches
A = 588 inches
Therefore Ed needs 588 tiles.
Page No. 746
Question 4.
Make Sense of Problems Lia has a dog and a cat. Together, the pets weigh 28 pounds. The dog weighs 3 times as much as the cat. How much does each pet weigh?
cat weight = _____ pounds dog weight = _____ pounds
Answer:
Given that, the pets weigh 28 pounds.
28 = 7 + 7 + 7 + 7
The dog weighs 3 times as much as the cat.
= 3 × 7 = 21 pounds
The dog weighs 21 pounds
28 – 21 = 7
The cat weighs = 7 pounds.
Question 5.
Mr. Foster is covering two rectangular pictures with glass. One is 6 inches by 4 inches and the other one is 5 inches by 5 inches. Does he need the same number of square inches of glass for each picture? Explain.
_____
Answer: No
Explanation:
Mr. Foster is covering two rectangular pictures with glass.
One is 6 inches by 4 inches and the other one is 5 inches by 5 inches.
Area of first rectangular picture = 6 × 4 = 24 square inches
Area of second rectangular picture = 5 × 5 = 25 square inches
Area of two rectangular pictures = 25 square inches – 24 square inches
1 square inch.
Therefore, he doesn’t need the same number of square inches of glass for each picture.
Question 6.
Claire says the area of a square with a side length of 100 centimeters is greater than the area of a square with a side length of 1 meter. Is she correct? Explain.
_____
Answer: No
Explanation:
Claire says the area of a square with a side length of 100 centimeters is greater than the area of a square with a side length of 1 meter.
Her statement is not correct because 1 meter = 100 centimeters.
So, the area of a square with a side length of 100 centimeters is equal to the area of a square with a side length of 1 meter.
Question 7.
A rectangular floor is 12 feet long and 11 feet wide. Janine places a rug that is 9 feet long and 7 feet wide and covers part of the floor in the room. Select the word(s) to complete the sentence.
To find the number of square feet of the floor that is NOT covered by the rug,
 the
the 
 the area of the floor.
the area of the floor.
_____ square feet
Answer:
Length = 12 feet
Width = 11 feet
Area of the rectangular floor = l × w
= 12 feet × 11 feet = 132 square feet
Room:
Length = 9 feet
Width = 7 feet
Area of the floor in the room = l × w
= 9 feet × 7 feet
= 63 square feet
Subtract the area of the rug from the area of the floor
= 132 square feet – 63 square feet = 69 square feet
The number of square feet of the floor that is NOT covered by the rug is 69 square feet.
Common Core – New – Page No. 747
Problem Solving Find the Area
Solve each problem.
Question 1.
A room has a wooden floor. There is a rug in the center of the floor. The diagram shows the room and the rug. How many square feet of the wood floor still shows?
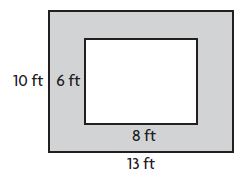
82 square feet
Area of the floor: 13 × 10 = 130 square feet
Area of the rug: 8 × 6 = 48 square feet
Subtract to find the area of the floor still showing: 130 – 48 = 82 square feet
Question 2.
A rectangular wall has a square window, as shown in the diagram.

What is the area of the wall NOT including the window?
The area of the wall NOT including the window = _____ square feet
Answer: 96 square feet
Explanation:
Wall:
Base = 14 feet
Height = 8 feet
Area of the wall = b × h
A = 14 feet × 8 feet
A = 112 square feet
Window:
Length = 4 feet
Area of the square = s × s
Area of the window = 4 feet × 4 feet = 16 square feet
Now subtract Area of the window from the area of the rectangular wall
= 112 square feet – 16 square feet
= 96 square feet
Therefore the area of the wall NOT including the window = 96 square feet.
Question 3.
Bob wants to put down new sod in his backyard, except for the part set aside for his flower garden. The diagram shows Bob’s backyard and the flower garden.
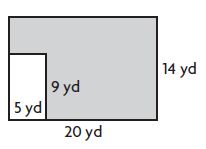
How much sod will Bob need?
The area covered with new sod = _____ square yards
Answer: 235 square yards
Flower Garden:
Base = 20 yards
Height = 14 yards
Area of the rectangular flower garden = b × h
A = 20 yards × 14 yards
A = 280 square yards
Sod:
Base = 5 yards
Height = 9 yards
Area of sod = b × h
= 5 yards × 9 yards = 45 square yards
Now subtract area of sod from area of flower garden
= 280 square yards – 45 square yards
= 235 square yards
Thus the area covered with new sod = 235 square yards
Question 4.
A rectangular painting is 24 inches wide and 20 inches tall without the frame. With the frame, it is 28 inches wide and 24 inches tall. What is the area of the frame not covered by the painting?
The area of the frame = _____ square inches
Answer: 192 square inches
Explanation:
A rectangular painting is 24 inches wide and 20 inches tall without the frame.
A = b × h
A = 24 inches × 20 inches
A = 480 square inches
With the frame, it is 28 inches wide and 24 inches tall.
A = b × h
A = 28 inches × 24 inches
A = 672 square inches
The area of the frame not covered by the painting
= 672 square inches – 480 square inches
= 192 square inches
Therefore, The area of the frame = 192 square inches
Question 5.
One wall in Jeanne’s bedroom is 13 feet long and 8 feet tall. There is a door 3 feet wide and 6 feet tall. She has a poster on the wall that is 2 feet wide and 3 feet tall. How much of the wall is visible?
The area of the wall visible = _____ square feet
Answer: 80 square feet
Explanation:
One wall in Jeanne’s bedroom is 13 feet long and 8 feet tall.
Area of Jeanne’s bedroom = 13 feet × 8 feet = 104 square feet
Area of door = 3 feet × 6 feet = 18 square feet
Area of the wall = 2 feet × 3 feet = 6 square feet
To find the area of the wall visible we have to subtract Area of the wall, Area of the door from Area of Jeanne’s bedroom.
104 square feet – 18 square feet – 6 square feet
= 80 square feet
The area of the wall visible = 80 square feet
Common Core – New – Page No. 748
Lesson Check
Question 1.
One wall in Zoe’s bedroom is 5 feet wide and 8 feet tall. Zoe puts up a poster of her favorite athlete. The poster is 2 feet wide and 3 feet tall. How much of the wall is not covered by the poster?
Options:
a. 16 square feet
b. 34 square feet
c. 35 square feet
d. 46 square feet
Answer: 34 square feet
Explanation:
One wall in Zoe’s bedroom is 5 feet wide and 8 feet tall.
Area of the wall in Zoe’s bedroom = b × h
A = 5 feet × 8 feet
A = 40 square feet
Zoe puts up a poster of her favorite athlete. The poster is 2 feet wide and 3 feet tall.
Area of the poster = b × h
A = 2 feet × 3 feet = 6 square feet
Now subtract Area of the poster from the Area of the wall in Zoe’s bedroom
= 40 square feet – 6 square feet
= 34 square feet
Thus the area of the wall is not covered by the poster = 34 square feet.
The correct answer is option B.
Question 2.
A garage door is 15 feet wide and 6 feet high. It is painted white, except for a rectangular panel 1 foot high and 9 feet wide that is brown. How much of the garage door is white?
Options:
a. 22 square feet
b. 70 square feet
c. 80 square feet
d. 81 square feet
Answer: 81 square feet
Explanation:
A garage door is 15 feet wide and 6 feet high.
Area of the garage door = b × h
A = 15 feet × 6 feet
A = 90 square feet
It is painted white, except for a rectangular panel 1 foot high and 9 feet wide that is brown.
b = 9 feet
h = 1 foot
A = b × h
A = 9 feet × 1 feet
A = 9 square feet
Area of the garage door is white = 90 square feet – 9 square feet
Area of the garage door is white = 81 square feet
The correct answer is option D.
Spiral Review
Question 3.
Kate baked a rectangular cake for a party. She used 42 inches of frosting around the edges of the cake. If the cake was 9 inches wide, how long was the cake?
Options:
a. 5 inches
b. 12 inches
c. 24 inches
d. 33 inches
Answer: 12 inches
Explanation:
Kate baked a rectangular cake for a party. She used 42 inches of frosting around the edges of the cake.
Width = 9 inches
P = (2 × l) + (2 × w)
42 inches = (2 × l) + (2 × 9)
(2 × l) + (2 × 9) = 42 inches
(2 × l) = 42 inches – 18 inches
2l = 24 inches
l = 24/2 = 12 inches
Therefore the cake is 12 inches long.
Thus the correct answer is option B.
Question 4.
Larry, Mary, and Terry each had a full glass of juice. Larry drank \(\frac{3}{4}\) of his. Mary drank \(\frac{3}{8}\) of hers. Terry drank \(\frac{7}{10}\) of his. Who drank less than \(\frac{1}{2}\) of their juice?
Options:
a. Larry
b. Mary
c. Mary and Terry
d. Larry and Terry
Answer: Mary
Explanation:
Larry, Mary, and Terry each had a full glass of juice.
Larry drank \(\frac{3}{4}\), Mary drank \(\frac{3}{8}\) and Terry drank \(\frac{7}{10}\) of \(\frac{1}{2}\)
\(\frac{3}{8}\) is less than \(\frac{1}{2}\) of their juice.
The correct answer is Option B.
Question 5.
Which of the following statements is NOT true about the numbers 7 and 9?
Options:
a. 7 is a prime number.
b. 9 is a composite number.
c. 7 and 9 have no common factors other than 1.
d. 27 is a common multiple of 7 and 9.
Answer: 27 is a common multiple of 7 and 9
Explanation:
a. 7 is a prime number is true.
b. 9 is a composite number is true
c. 7 and 9 have no common factors other than 1 is true.
d. 27 is a common multiple of 7 and 9 is not true because 7 is not the multiple of 27.
Thus the correct answer is option D.
Question 6.
Tom and some friends went to a movie. The show started at 2:30 P.M. and ended at 4:15 P.M. How long did the movie last?
Options:
a. 1 hour 35 minutes
b. 1 hour 45 minutes
c. 1 hour 55 minutes
d. 2 hours 15 minutes
Answer: 1 hour 45 minutes
Explanation:
Tom and some friends went to a movie. The show started at 2:30 P.M. and ended at 4:15 P.M.
Subtract 2:30 P.M. from 4:15 P.M.
4 hour 15 minutes
-2 hour 30 minutes
1 hour 45 minutes
The movie last for 1 hour 45 minutes
Thus the correct answer is option B.
Page No. 749
Question 1.
For numbers 1a–1e, select Yes or No to indicate if a rectangle with the given dimensions would have a perimeter of 50 inches.
a. length: 25 inches; width: 2 inches
i. yes
ii. no
Answer: No
Explanation:
P = (2 × l) + (2 × w)
50 inches = (2 × 25 in.) + (2 × w)
(2 × w) = 50 inches – 50 inches
w = 0
Thus the above statement is false
Question 1.
b. length: 20 inches; width: 5 inches
i. yes
ii. no
Answer: Yes
Explanation:
P = (2 × l) + (2 × w)
50 inches = (2 × 20 in.) + (2 × 5)
50 inches = 40 in. + 10 in.
Thus the above statement is true.
Question 1.
c. length: 17 inches; width: 8 inches
i. yes
ii. no
Answer: Yes
Explanation:
P = (2 × l) + (2 × w)
50 inches = (2 × 17 in.) + (2 × 8 in.)
50 inches = 34 in. + 16 in.
Thus the above statement is true.
Question 1.
d. length: 15 inches; width: 5 inches
i. yes
ii. no
Answer: No
Explanation:
P = (2 × l) + (2 × w)
50 inches = (2 × 15 in.) + (2 × 5 in.)
50 inches = 30 in. + 10 in.
50 inches = 40 inches
Thus the above statement is false.
Question 1.
e. length: 15 inches; width: 10 inches
i. yes
ii. no
Answer: Yes
Explanation:
P = (2 × l) + (2 × w)
50 inches = (2 × 15 in.) + (2 × 10 in.)
50 inches = 30 in. + 20 in.
50 inches = 50 inches
Thus the above statement is true.
Question 2.
The swimming club’s indoor pool is in a rectangular building.
Marco is laying tile around the rectangular pool.
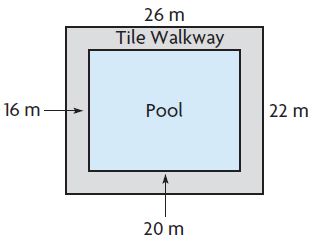
Part A
What is the area of the pool and the area of the pool and the walkway? Show your work.
A(pool) = ____ m2 A(building) = ____ m2
Answer:
Pool:
Base = 20 m
Height = 16 m
A = b × h
Area of the pool = 20 m × 16 m = 320 square meters
Pool and the walkway:
Area of the pool and the walkway = 26 m × 22 m = 572 square meters
Question 2.
Part B
How many square meters of tile will Marco need for the walkway?
Explain how you found your answer.
A(walkway) = ____ m2
Answer: 252 square meters
Explanation:
Area of walkway = Area of the pool and the walkway – Area of pool
Area of the walkway = 572 square meters – 320 square meters
= 252 square meters
Therefore the Area of walkway = 252 square meters
Page No. 750
Question 3.
Match the dimensions of the rectangles in the top row with the correct area or perimeter in the bottom row
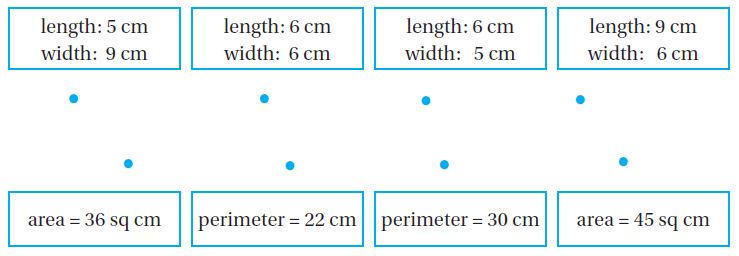
Answer:

Question 4.
Kyleigh put a large rectangular sticker on her notebook. The height of the sticker measures 18 centimeters. The base is half as long as the height. What area of the notebook does the sticker cover?
________ square centimeters
Answer: 162 square centimeters
Explanation:
Kyleigh put a large rectangular sticker on her notebook.
The height of the sticker measures 18 centimeters.
The base is half as long as the height.
Base = h/2 = 18/2 = 9 centimeters
Area of the rectangle = b × h
A = 9 cm × 18 cm
A = 162 square centimeters
Thus the area of the notebook the sticker cover is 162 square centimeters.
Question 5.
A rectangular flower garden in Samantha’s backyard has 100 feet around its edge. The width of the garden is 20 feet. What is the length of the garden? Use the numbers to write an equation and solve. A number may be used more than once.

□ = (2 × l) + (2 × □)
□ = 2 × l + □
□ = 2 × l
□ = l
So, the length of the garden _____ feet.
Answer:
P = (2 × l) + (2 × w)
100 = (2 × l) + (2 × 20)
100 – 40 = 2 × l
2 × l = 60
l = 60/2 = 30 feet
Length = 30 feet
So, the length of the garden 30 feet.
Question 6.
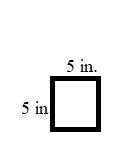
Gary drew a rectangle with a perimeter of 20 inches. Then he tried to draw a square with a perimeter of 20 inches.
Draw 3 different rectangles that Gary could have drawn. Then draw the square, if possible.
Type below:
__________
Answer:
The possible rectangles with a perimeter of 20 inches are:
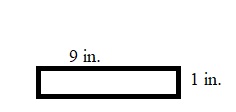
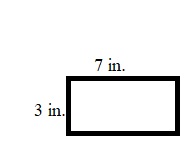
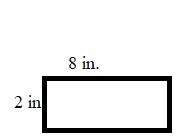
The possible square with a perimeter of 20 inches is:
Page No. 751
Question 7.
Ami and Bert are drawing plans for rectangular vegetable gardens. In Ami’s plan, the garden is 13 feet by 10 feet. In Bert’s plan, the garden is 12 feet by 12 feet. For numbers 7a−7d, select True or False for each statement.
a. The area of Ami’s garden is 130 square feet.
i. True
ii. False
Answer: True
Explanation:
A = b × h
Area of Ami’s garden = 13 feet × 10 feet =
Area of Ami’s garden = 130 square feet
The above statement is true.
Question 7.
b. The area of Bert’s garden is 48 square feet.
i. True
ii. False
Answer: False
Explanation:
Area of Bert’s garden = 12 feet × 12 feet = 144 square feet
The above statement is false.
Question 7.
c. Ami’s garden has a greater area than Bert’s garden.
i. True
ii. False
Answer: False
Explanation:
Area of Ami’s garden = 13 feet × 10 feet = 130 square feet
Area of Bert’s garden = 12 feet × 12 feet = 144 square feet
130 square feet is less than 144 square feet
The area of Ami’s garden is less than Area of Bert’s garden.
The above statement is false.
Question 7.
d. The area of Bert’s garden is 14 square feet greater than Ami’s.
i. True
ii. False
Answer: True
Explanation:
Area of Ami’s garden = 13 feet × 10 feet = 130 square feet
Area of Bert’s garden = 12 feet × 12 feet = 144 square feet
144 square feet – 130 square feet = 14 square feet
The above statement is true.
Question 8.
A farmer planted corn in a square field. One side of the field measures 32 yards. What is the area of the cornfield? Show your work.
_______ square yards
Answer: 1024 square yards
Explanation:
A farmer planted corn in a square field. One side of the field measures 32 yards.
Area of the square = 32 yards × 32 yards
A = 1,024 square yards
Therefore the area of the cornfield is 1,024 square yards.
Question 9.
Harvey bought a frame in which he put his family’s picture.
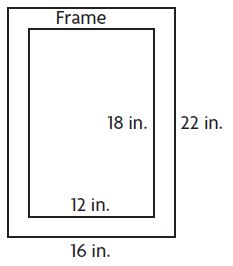
What is the area of the frame not covered by the picture?
_______ square inches
Answer: 136 square inches
Explanation:
Area of the picture = 12 in. × 18 in.
A = 216 square inches
Area of the frame = 16 in. × 22 in.
A = 352 square inches
The area of the frame not covered by the picture = 352 square inches – 216 square inches
= 136 square inches
Therefore the area of the frame not covered by the picture is 136 square inches.
Question 10.
Kelly has 236 feet of fence to use to enclose a rectangular space for her dog. She wants the width to be 23 feet. Draw a rectangle that could be the space for Kelly’s dog. Label the length and width.
Type below:
________
Answer:
Kelly has 236 feet of fence to use to enclose a rectangular space for her dog.
She wants the width to be 23 feet.
Perimeter = (2 × l) + (2 × w)
236 = (2 × l) + (2 × w)
236 = (2 × l) + (2 × 23)
236 – 46 = (2 × l)
(2 × l) = 190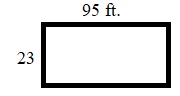
l = 190/2
l = 95 feet
Therefore length = 95 feet.
Page No. 752
Question 11.
The diagram shows the dimensions of a new parking lot at Helen’s Health Food store.
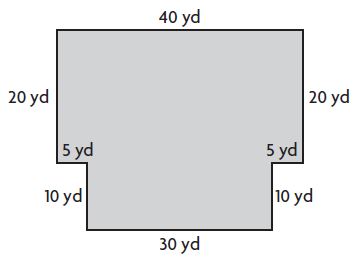
Use either addition or subtraction to find the area of the parking lot. Show your work.
_______ square yards
Answer: 1100 square yards
Explanation:
Addition:
Top:
Base = 40 yards
Height = 20 yards
Area of the top rectangle = b × h
A = 40 yards × 20 yards = 800 square yards
Bottom:
Base = 30 yards
Height = 10 yards
Area of the rectangle = b × h
A = 30 yards × 10 yards = 300 square yards
Area of the parking = Area of top + Area of bottom
A = 800 square yards + 300 square yards
Area of parking = 1100 square yards.
Question 12.
Chad’s bedroom floor is 12 feet long and 10 feet wide. He has an area rug on his floor that is 7 feet long and 5 feet wide. Which statement tells how to find the amount of the floor that is not covered by the rug? Mark all that apply.
Options:
a. Add 12 × 10 and 7 × 5.
b. Subtract 35 from 12 × 10
c. Subtract 10 × 5 from 12 × 7.
d. Add 12 + 10 + 7 + 5.
e. Subtract 7 × 5 from 12 × 10.
f. Subtract 12 × 10 from 7 × 5.
Answer: B, F
Chad’s bedroom floor is 12 feet long and 10 feet wide.
A = 12 feet × 10 feet = 120 square feet
Area rug on his floor = 7 feet × 5 feet = 35 square feet
To find the amount of the floor that is not covered by the rug we have to subtract 120 square feet from 35 square feet or 35 square feet from 12 × 10.
So, the correct answers are B and F.
Question 13.
A row of plaques covers 120 square feet of space along a wall. If the plaques are 3 feet tall, what length of the wall do they cover?
____ feet
Answer: 40 feet
Explanation:
Given that,
A row of plaques covers 120 square feet of space along a wall.
Height = 3 feet
A = b × h
120 square feet = b × 3 feet
b = 120/3 = 40
Therefore the base is 40 feet.
Page No. 753
Question 14.
Ms. Bennett wants to buy carpeting for her living room and dining room.

Explain how she can find the amount of carpet she needs to cover the floor in both rooms. Then find the amount of carpet she will need.
____ square feet
Answer:
She can find the area of each rectangle and then find the sum. The area of the living room is 20 × 20 = 400 square feet.
The area of the dining room is 15 × 10 = 150 square feet.
The sum of the two rooms = 400 + 150 = 550 square feet.
She needs 550 square feet of carpeting.
Question 15.
Lorenzo built a rectangular brick patio. He is putting a stone border around the edge of the patio. The width of the patio is 12 feet. The length of the patio is two feet longer than the width.
How many feet of stone will Lorenzo need? Explain how you found your answer.
____ feet
Answer: 52 feet
Explanation:
Width = 12 feet
Length = 2 × width
Length = 2 + 12 feet = 14 feet
Perimeter = (2 × l) + (2 × w)
P = (2 × 14) + (2 × 12)
P = 28 + 24
P = 52 feet
Page No. 754
Question 16.
Which rectangle has a perimeter of 10 feet? Mark all that apply.
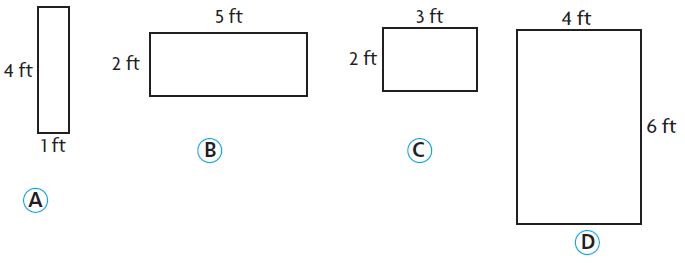
Rectangle: ____
Rectangle: ____
Answer: A, C
Explanation:
i. Perimeter of A = (2 × l) + (2 × w)
P = (2 × 1) + (2 × 4) = 2 + 8 = 10 feet
ii. Perimeter of B = (2 × l) + (2 × w)
P = (2 × 2) + (2 × 5) = 4 + 10 = 14 feet
iii. Perimeter of C = (2 × l) + (2 × w)
P = (2 × 2) + (2 × 3) = 4 + 6 = 14 feet
iv. Perimeter of D = (2 × l) + (2 × w)
P = (2 × 4) + (2 × 6) = 8 + 12 = 20 feet
The correct answer is option A and C.
Question 17.
A folder is 11 inches long and 8 inches wide. Alyssa places a sticker that is 2 inches long and 1 inch wide on the notebook. Choose the words that correctly complete the sentence.
To find the number of square inches of the folder that is NOT covered by the sticker,

Type below:
________
Answer: Subtract the area of the sticker from the area of the notebook.
Question 18.
Tricia is cutting her initial from a piece of felt. For numbers 18a–18c, select Yes or No to tell whether you can add the products to find the number of square centimeters Tricia needs.

a. 1 × 8 and 5 × 2 _______
b. 3 × 5 and 1 × 8 _______
c. 2 × 5 and 1 × 3 and 1 × 3 _______
Answer:
a. 1 × 8 and 5 × 2 _______
Yes
b. 3 × 5 and 1 × 8 _______
No
c. 2 × 5 and 1 × 3 and 1 × 3 _______
No
Question 19.
Mr. Butler posts his students’ artwork on a bulletin board.

The width and length of the bulletin board are whole numbers. What could be the dimensions of the bulletin board Mr. Butler uses?
Type below:
________
Answer: 5 feet long by 3 feet wide
Area of the rectangle = l × w
A = 15 square feet
The factor of 15 is 5 and 3.
So, the length = 5 feet long
Width = 3 feet long.
Quick learning is not only important but also understanding is important to learn the concepts. You can’t love maths if you don’t understand the subject. So, to help you guys we have provided the images for your better understanding. Learn the simple techniques to solve the problem in less time in our Go Math Answer Key.
Conclusion:
Hope you are satisfied with the solutions provided in the Go Math Grade 4 Answer Key Chapter 13 Algebra: Perimeter and Area. For unlimited practice check out the questions in the review at the end of the chapter. You can also find all chapter’s solutions in our Go Math Answer Key. Make use of the links and score the highest marks in the exams. Best Of Luck!!!!
