Go Math Grade 4 Chapter 11 Answer Key Pdf Angles

Go Math Grade 4 Chapter 11 Answer Key Pdf: Students who are looking for quick learning with basic fundamentals can Download Go Math Grade 4 Answer Key Chapter 11 Angles pdf for free. There are different types of questions with detailed and simple explanations here. So, the students of Grade 4 can make HMH Go Math Answer Key as a reference while practicing the problems. There is a scope to learn simple techniques to solve the problems. Go Math Grade 4 Answer Key helps the parents to explain the concepts in an easy manner to their children.

Angles Go Math Grade 4 Chapter 11 Answer Key Pdf

We have provided the solutions for not only the exercised but also for the mid-chapter checkpoint and review tests. So, the students can check the solutions after practicing from Go Math Grade Chapter 11 Answer Key. Check out the topics given below before starting your preparation. Get step by step procedure for each and every problem with suitable examples in our Go Math Answer Key for Grade 4 Chapter 11 Angles. Hence make use of the links and start practicing now.

Lesson 1:

• Investigate • Angles and Fractional Parts of a Circle Page No. 605
• Investigate • Angles and Fractional Parts of a Circle Lesson Check Page No. 606

Lesson 2:

• Degrees Page No. 609
• Degrees Lesson Check Page No. 610

Lesson 3: Measure and Draw Angles

• Common Core – New Measure and Draw Angles Page No. 611
• Common Core – New Measure and Draw Angles Lesson Check Page No. 612
• Measure and Draw Angles Page No. 615
• Measure and Draw Angles Page No. 616
• Measure and Draw Angles Page No. 617
• Measure and Draw Angles Lesson Check Page No. 618

Mid-Chapter Checkpoint

• Mid-Chapter Checkpoint Page No. 619
• Mid-Chapter Checkpoint Lesson Check Page No. 620

Lesson 4:

• Investigate • Join and Separate Angles Page No. 623
• Investigate • Join and Separate Angles Lesson Check Page No. 624

Common Core – New

• Common Core – New – Page No. 625
• Common Core – New Lesson Check – Page No. 626

Lesson 5:

• Problem Solving • Unknown Angle Measures Page No. 629
• Problem Solving • Unknown Angle Measures Page No. 630

Common Core – New

• Problem Solving Unknown Angle Measures Common Core – New – Page No. 631
• Problem Solving Unknown Angle Measures Common Core – New Lesson Check – Page No. 632

Chapter 11 Review/Test

• Review/Test Page No. 633
• Review/Test Page No. 634
• Review/Test Page No. 635
• Review/Test Page No. 636
• Review/Test Page No. 637
• Review/Test Page No. 638
• Review/Test Page No. 643
• Review/Test Page No. 644

Common Core – New – Page No. 605

Angles and Fractional Parts of a Circle

Tell what fraction of the circle the shaded angle represents.

Question 1.

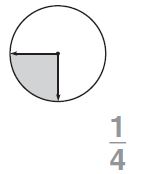
The figure shows that the \(\frac{1}{4}\)th part of the circle is shaded. So, the fraction of the shaded angle is \(\frac{1}{4}\)

Question 2.

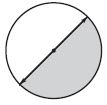
\(\frac{□}{□}\)

Answer: \(\frac{1}{2}\)

Explanation:

Half of the circle is shaded. Thus the fraction of the shaded angle is \(\frac{1}{2}\)

Question 3.

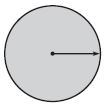
\(\frac{□}{□}\)

Answer: \(\frac{1}{1}\)

Explanation:

From the above figure, we can observe that the complete circle is shaded. So, the fraction of the shaded angle is \(\frac{1}{1}\) or 1.

Tell whether the angle on the circle shows a \(\frac{1}{4}, \frac{1}{2}, \frac{3}{4}\), or 1 full turn clockwise or counterclockwise.

Question 4.

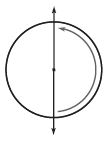
\(\frac{□}{□}\)

Answer: \(\frac{1}{2}\) turn counter clockwise

Explanation:

From the figure, we can see that the circle is rotating in the anti-clockwise direction. And it has completed the half turn.
Thus the fraction is \(\frac{1}{2}\) turn counter clockwise

Question 5.

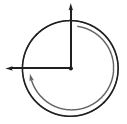
\(\frac{□}{□}\)

Answer: \(\frac{3}{4}\) turn clockwise

Explanation:

The arrow is turned in a clockwise direction. It has completed \(\frac{3}{4}\) turn. So, the angle with direction is \(\frac{3}{4}\) turn clockwise.

Question 6.

_________

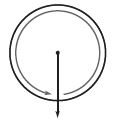
Answer: 1 full turn counter clockwise

Explanation:

From the above picture, we can observe that the circle has completed the full turn in the counter clockwise direction.

Problem Solving

Question 7.
Shelley exercised for 15 minutes. Describe the turn the minute hand made.

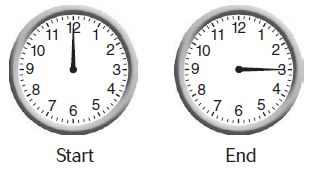
Type below:
_________

Answer: The minute hand made a turn of \(\frac{1}{4}\) clockwise.

Explanation:

Given that,

Shelley exercised for 15 minutes.
So, the fraction of the minute hand made is \(\frac{1}{4}\).
The direction of the minute hand made is clockwise.
So, the answer is the minute hand made a turn of \(\frac{1}{4}\) clockwise.

Question 8.
Mark took 30 minutes to finish lunch. Describe the turn the minute hand made.

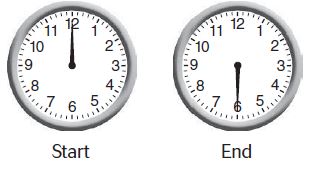
Type below:
_________

Answer: The minute hand made a turn of \(\frac{1}{2}\) clockwise.

Explanation:

Given, Mark took 30 minutes to finish lunch.
The minute hand made a turn in the clockwise direction from 12 to 6.
That means the fraction of the angle is \(\frac{1}{2}\).
Thus the turn minute hand made is \(\frac{1}{2}\) clockwise.

Common Core – New – Page No. 606

Lesson Check

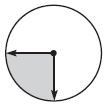
Question 1.
What fraction of the circle does the shaded angle represent

Options:
a. \(\frac{1}{1}\) or 1
b. \(\frac{3}{4}\)
c. \(\frac{1}{2}\)
d. \(\frac{1}{4}\)

Answer: \(\frac{1}{4}\)

Explanation:

From the figure we can say that the fraction of the shaded angle is \(\frac{1}{4}\).
Thus the answer is option D.

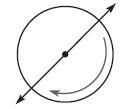
Question 2.
Which describes the turn shown below?

Options:
a. \(\frac{1}{4}\) turn clockwise
b. \(\frac{1}{2}\) turn clockwise
c. \(\frac{1}{4}\) turn counterclockwise
d. \(\frac{1}{2}\) turn counterclockwise

Answer: \(\frac{1}{2}\) turn clockwise

Explanation:

From the figure, we can see that the circle is rotating in the clockwise direction. And it has completed the half turn.
So, the answer is \(\frac{1}{2}\) turn clockwise.

Spiral Review

Question 3.
Which shows \(\frac{2}{3}\) and \(\frac{3}{4}\) written as a pair of fractions with a common denominator?
Options:
a. \(\frac{2}{3} \text { and } \frac{4}{3}\)
b. \(\frac{6}{9} \text { and } \frac{6}{8}\)
c. \(\frac{2}{12} \text { and } \frac{3}{12}\)
d. \(\frac{8}{12} \text { and } \frac{9}{12}\)

Answer: \(\frac{8}{12} \text { and } \frac{9}{12}\)

Explanation:

\(\frac{2}{3}\) and \(\frac{3}{4}\)
The denomintors are different here. So you have to make the denominators common.
\(\frac{2}{3}\) × \(\frac{4}{4}\) = \(\frac{8}{12}\)
\(\frac{3}{4}\) × \(\frac{3}{3}\) = \(\frac{9}{12}\)
So the answer is option D.

Question 4.
Raymond bought \(\frac{3}{4}\) of a dozen rolls. How many rolls did he buy?
Options:
a. 3
b. 6
c. 7
d. 9

Answer: 9

Explanation:

Raymond bought \(\frac{3}{4}\) of a dozen rolls.
Dozen = 12
\(\frac{3}{4}\) × 12 = 9
Thus the correct answer is option D.

Question 5.
Which of the following lists all the factors of 18?
Options:
a. 1, 2, 4, 9, 18
b. 1, 2, 3, 6, 9, 18
c. 2, 3, 6, 9
d. 1, 3, 5, 9, 18

Answer: 1, 2, 3, 6, 9, 18

Explanation:

The factors of 18 are
1 × 18 = 18
2 × 9 = 18
3 × 6 = 18
6 × 3 = 18
9 × 2 = 18
18 × 1 = 18
Thus the correct answer is option B.

Question 6.
Jonathan rode 1.05 miles on Friday, 1.5 miles on Saturday, 1.25 miles on Monday, and 1.1 miles on Tuesday. On which day did he ride the shortest distance?
Options:
a. Monday
b. Tuesday
c. Friday
d. Saturday

Answer: Friday

Explanation:

Jonathan rode 1.05 miles on Friday, 1.5 miles on Saturday, 1.25 miles on Monday, and 1.1 miles on Tuesday.
The shortest among all is 1.05 miles.
Therefore the answer is option C.

Page No. 609

Question 1.
Find the measure of the angle.

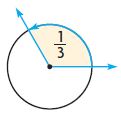
Through what fraction of a circle does the angle turn?
\(\frac{1}{3}=\frac{■}{360}\)
Think: 3 × 12 = 36, so 3 × _____ = 360.
So, the measure of the angle is _____.
_____ degrees

Answer: 120°

Explanation:

The fraction of the shaded angle is \(\frac{1}{3}\)
To measure the angle we have to multiply the fraction of the shaded angle with the total angle.
That means, \(\frac{1}{3}\) × 360
360/3 = 120 degrees.
Thus the angle of the shaded part is 120°

Tell the measure of the angle in degrees.

Question 2.

____ °

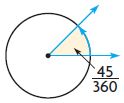
Answer: 45°

Explanation:

The fraction of the shaded angle is \(\frac{45}{360}\)
Multiply the fraction with the complete angle
\(\frac{45}{360}\) × 360° = 45°
Thus the angle of the above figure is 45°

Question 3.

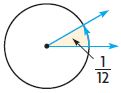
____ degrees

Answer: 30°

Explanation:

The figure shows the fraction of the shaded angle is \(\frac{1}{12}\)
Multiply the fraction with the complete angle
\(\frac{1}{12}\) × 360° = 30°
Therefore the measure of the shaded angle is 30°

Tell the measure of the angle in degrees.

Question 4.

____ °

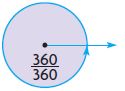
Answer: 360°

Explanation:

We observe that the circle is shaded completely.
\(\frac{360}{360}\) × 360° = 360°
Thus the above figure is the complete angle.

Question 5.

____ °

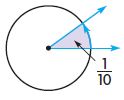
Answer: 36°

Explanation:

The fraction of the shaded angle is \(\frac{1}{10}\)
Multiply the fraction with the complete angle
\(\frac{1}{10}\) × 360° = 36°
Therefore the measure of the shaded angle is 36°

Classify the angle. Write acute, obtuse, right, or straight.

Question 6.

_________

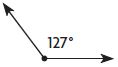
Answer: Obtuse

An obtuse angle has a measurement greater than 90 degrees but less than 180 degrees. However, A reflex angle measures more than 180 degrees but less than 360 degrees.

Question 7.

_________

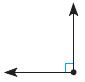
Answer: Right

A right angle is an angle of exactly 90° (degrees), corresponding to a quarter turn. If a ray is placed so that its endpoint is on a line and the adjacent angles are equal, then they are right angles.

Question 8.

_________

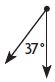
Answer: Acute

The acute angle is the small angle which is less than 90°.

Question 9.

_________

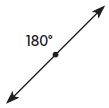
Answer: Straight

A straight angle is 180 degrees. A straight angle changes the direction to point the opposite way.

Question 10.
Is this an obtuse angle? Explain.

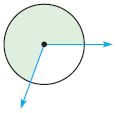
Type below:
_________

Answer: Obtuse

An obtuse angle has a measurement greater than 90 degrees but less than 180 degrees. However, A reflex angle measures more than 180 degrees but less than 360 degrees.

Question 11.
Alex cut a circular pizza into 8 equal slices. He removed 2 of the slices of pizza. What is the measure of the angle made by the missing slices of pizza?

____ °

Answer: 90°

Explanation:

Alex cut a circular pizza into 8 equal slices.
He removed 2 of the slices of pizza.
The fraction of the missing slices = \(\frac{2}{8}\) = \(\frac{1}{4}\)
The fraction of the missing slices is \(\frac{1}{4}\)
To know the angle we have to multiply the fraction with complete angle i.e., 360°
\(\frac{1}{4}\) × 360° = 90°
Thus the angle of the missing slices is 90°

Page No. 610

Question 12.
Ava started reading at 3:30 p.m. She stopped for a snack at 4:15 p.m. During this time, through what fraction of a circle did the minute hand turn? How many degrees did the minute hand turn?

a. What are you asked to find?
Type below:
_________

Answer: I am asked to find the fraction of a circle did the minute hand turn and how many degrees did the minute hand turn

Question 12.
b. What information can you use to find the fraction of a circle through which the minute hand turned?
Type below:
_________

Answer: The fraction of a circle through which the minute hand-turned \(\frac{3}{4}\) Clockwise.

Question 12.
c. How can you use the fraction of a circle through which the minute hand turned to find how many degrees it turned?
Type below:
_________

Answer:

The figure shows that the fraction of a circle through which the minute hand turned is \(\frac{3}{4}\) Clockwise.
Let the shaded part be x
And the nonshaded part is 90°
x + 90° = 360°
x = 360°- 90°
x = 270°
Therefore the minute hand turns 270° clockwise.

Question 12.
d. Show the steps to solve the problem.
Step 1:
\(\frac{3 × ■}{4 × ■}=\frac{?}{360}\)
Step 2:
\(\frac{3 × 90}{4 × 90}=\frac{■}{360}\)
Type below:
_________

Answer:
\(\frac{3 × 90}{4 × 90}=\frac{■}{360}\)
\(\frac{270}{360} = \frac{■}{360}\)
If the denominators are equal then the numerators must be equated.
■ = 270

Question 12.
e. Complete the sentences. From 3:30 p.m. to 4:15 p.m., the minute hand made a ______ turn clockwise. The minute hand turned ______ degrees.
Type below:
_________

Answer:
From 3:30 p.m. to 4:15 p.m., the minute hand made a \(\frac{3}{4}\) turn clockwise. The minute hand turned 270 degrees.

Question 13.
An angle represents \(\frac{1}{15}\) of a circle. Select the number to show how to find the measure of the angle in degrees.


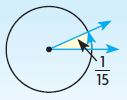
\(\frac{1}{15}=\frac{1 × □}{15 × □}=\frac{□}{360}\)
Type below:
_________

Answer: 24°
\(\frac{1}{15} × 360° = 24°

Common Core – New – Page No. 611

Degrees

Tell the measure of the angle in degrees.

Question 1.

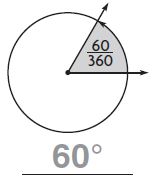
Answer: 60°

Explanation:

Given that the fraction of the shaded angle is [latex]\frac{60}{360}\)
\(\frac{60}{360}\) × 360 = 60°
Thus the angle for the above figure is 60°

Question 2.

____ °

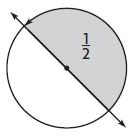
Answer: 180°

Explanation:

Half of the circle is shaded. The fraction of the shaded angle is \(\frac{1}{2}\)
\(\frac{1}{2}\) × 360 = 360/2 = 180°

Question 3.

____ °

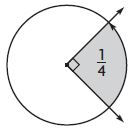
Answer: 90°

Explanation:

The fraction of the shaded angle is \(\frac{1}{4}\)
To find the angle we need to multiply the fraction with the total angle.
\(\frac{1}{4}\) × 360° = 90°

Classify the angle. Write acute, obtuse, right, or straight.

Question 4.

_________

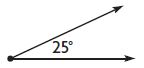
Answer: Acute

Explanation:

25° < 90°
So, the above figure is an acute angle.

Question 5.

_________

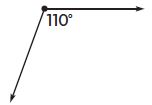
Answer: Obtuse

Explanation:

110° > 90°
So, the figure shown above is an obtuse angle.

Question 6.

_________

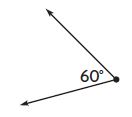
Answer: Acute

Explanation:

60° < 90°
Acute angles measure less than 90 degrees. Thus the above angle is an acute angle.

Classify the triangle. Write acute, obtuse, or right.

Question 7.

_________

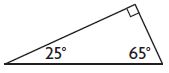
Answer: Right

Explanation:

65 + 25 = 90
The sum of two angles = 90°
Thus the above figure is a right-angled triangle.

Question 8.

_________

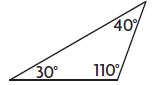
Answer: Obtuse

Explanation:

110° > 90°
So, the above triangle is an obtuse angle.

Question 9.

_________

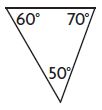
Answer: Acute

Explanation:

50° is less than 90°
Thus the above triangle is an acute angle triangle.

Problem Solving

Ann started reading at 4:00 P.M. and finished at 4:20 P.M.

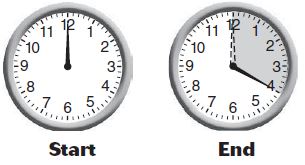
Question 10.
Through what fraction of a circle did the minute hand turn?
\(\frac{□}{□}\)

Answer: \(\frac{1}{3}\) turn clockwise

Explanation:

The fraction of the shaded clock is \(\frac{12}{4}\)
\(\frac{12}{4}\) = \(\frac{1}{3}\)
The minute hand turn clockwise direction.
So, the answer is \(\frac{1}{3}\) turn clockwise

Question 11.
How many degrees did the minute hand turn?
____ °

Answer: 120°

Explanation:

The fraction of the minute hand turn is \(\frac{1}{3}\)
\(\frac{1}{3}\) × 360° = 120°
The minute hand turn 120°

Common Core – New – Page No. 612

Lesson Check

Question 1.
What kind of angle is shown?

Options:
a. acute
b. obtuse
c. right
d. straight

Answer: straight

A straight angle is 180 degrees. This is a straight angle. A straight angle changes the direction to point the opposite way.
So, the answer is option D.

Question 2.
How many degrees are in an angle that turns through \(\frac{1}{4}\) of a circle?
Options:
a. 45°
b. 90°
c. 180°
d. 270°

Answer: 90°

Explanation:

\(\frac{1}{4}\) × 360°
\(\frac{360}{4}\) = 90°
Thus the correct answer is option B.

Spiral Review

Question 3.
Mae bought 15 football cards and 18 baseball cards. She separated them into 3 equal groups. How many sports cards are in each group?
Options:
a. 5
b. 6
c. 11
d. 12

Answer: 11

Explanation:

Mae bought 15 football cards and 18 baseball cards.
She separated them into 3 equal groups.
Total number of cards = 15 + 18 = 33
33/3 = 11
There are 11 sports cards in each group.

Question 4.
Each part of a race is \(\frac{1}{10}\) mile long. Marsha finished 5 parts of the race. How far did Marsha race?
Options:
a. \(\frac{1}{10}\) mile
b. \(\frac{5}{12}\) mile
c. \(\frac{1}{2}\) mile
d. 5 \(\frac{1}{10}\) miles

Answer: \(\frac{1}{2}\) mile

Explanation:

Each part of a race is \(\frac{1}{10}\) mile long.
Marsha finished 5 parts of the race.
\(\frac{1}{10}\) × 5 = 5/10 = \(\frac{1}{2}\) mile
Thus the correct answer is option C.

Question 5.
Jeff said his city got \(\frac{11}{3}\) inches of snow. Which shows this fraction written as a mixed number?
Options:
a. 3 \(\frac{2}{3}\)
b. 3 \(\frac{1}{3}\)
c. 2 \(\frac{2}{3}\)
d. 1 \(\frac{2}{3}\)

Answer: 3 \(\frac{2}{3}\)

Explanation:

Jeff said his city got \(\frac{11}{3}\) inches of snow.
The mixed fraction of \(\frac{11}{3}\) is 3 \(\frac{2}{3}\)
The correct answer is option A.

Question 6.
Amy ran \(\frac{3}{4}\) mile. Which decimal shows how many miles she ran?
Options:
a. 0.25 mile
b. 0.34 mile
c. 0.5 mile
d. 0.75 mile

Answer: 0.75 mile

Explanation:

Amy ran \(\frac{3}{4}\) mile.
\(\frac{3}{4}\) = \(\frac{75}{100}\)
The decimal form of \(\frac{75}{100}\) is 0.75
So, the answer is option D.

Page No. 615

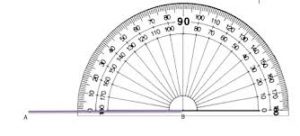
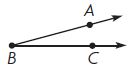
Question 1.
Measure ∠ABC.

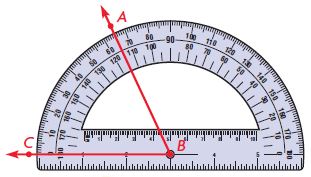
Place the center of the protractor on point ____.
Align ray BC with ____ .
Read where ____ intersects the same scale.
So, m∠ABC is _____.
Type below:
_________

Answer: 65°

Use a protractor to find the angle measure.

Question 2.

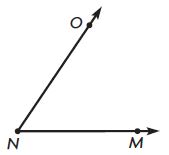
m∠ONM = ____ °

Answer: 55°

Question 3.

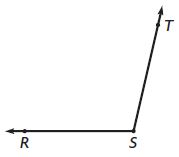
m∠TSR = ____ °

Answer: 105°

Use a protractor to draw the angle.

Question 4.
170°
Type below:
_________

Answer:

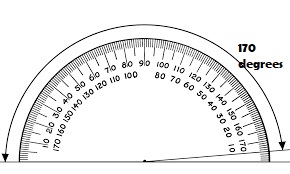
Question 5.
78°
Type below:
_________

Answer:

Use a protractor to find the angle measure.

Question 6.

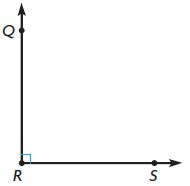
m∠QRS = ____ °

Answer: 90°

Question 7.

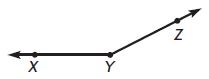
m∠XYZ = ____ °

Answer: 155°

Use a protractor to draw the angle.

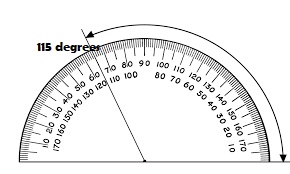
Question 8.
115°
Type below:
_________

Answer:

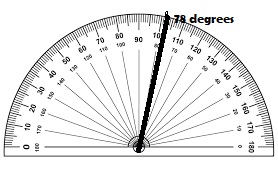
Question 9.
67°
Type below:
_________

Answer:

Draw an example of each. Label the angle with its measure.

Question 10.
an acute angle
Type below:
_________

Answer:

Question 11.
an obtuse angle
Type below:
_________

Answer:

Question 12.
Elizabeth is making a quilt with scraps of fabric. What is the difference between m∠ABC and m∠DEF?

____ °

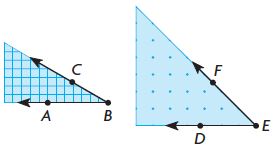
Answer: 15°

Question 13.
Draw an angle with a measure of 0°.
Describe your drawing.
Type below:
_________

Answer:

Page No. 616

Question 14.
Hadley wants to divide this angle into three angles with equal measure. What will the measure of each angle be?

____ °

Answer: 30°

Explanation:

Given,
Hadley wants to divide this angle into three angles with equal measure.
The above figure is a right angle = 90°
If he divides into three equal angles
90/3 = 30°
So, the measure of angle will be 30°

Question 15.
Tracy measured an angle as 50° that was actually 130°. Explain her error.
Type below:
_________

Answer: She has measured the angle in the counterclockwise direction. So, that is why she got 50°.

Question 16.
Choose the word or number to complete a true statement about ∠QRS.

∠QRS is a(n) angle that has a measure of
Type below:
_________

Answer: ∠QRS is an obtuse angle that has a measure of 135°.

Earth’s Axis Earth revolves around the sun yearly. The Northern Hemisphere is the half of Earth that is north of the equator. The seasons of the year are due to the tilt of Earth’s axis.

Use the diagrams and a protractor for 17–18.

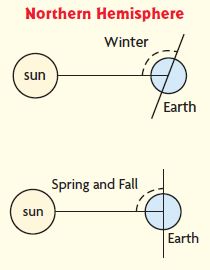
Question 17.
In the Northern Hemisphere, Earth’s axis is tilted away from the sun on the first day of winter, which is often on December 21. What is the measure of the marked angle on the first day of winter, the shortest day of the year?
____ °

Answer: 115°

Explanation:

By seeing the above figure we can say that the angle is an obtuse angle. The mark is above 90° and the marked angle is 115°.
Therefore the measure of the marked angle on the first day of winter, the shortest day of the year is 115°.

Question 18.
Earth’s axis is not tilted away from or toward the sun on the first days of spring and fall, which are often on March 20 and September 22. What is the measure of the marked angle on the first day of spring or fall?
____ °

Answer: 90°

Explanation:

The mark is exactly 90°. So, the angle on the first day of spring or fall is 90°

Common Core – New – Page No. 617

Measure and Draw Angles

Use a protractor to find the angle measure.

Question 1.

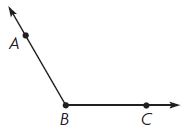
m∠ABC = 120°

By using the protractor we can measure the angle m∠ABC i.e., 120°

Question 2.

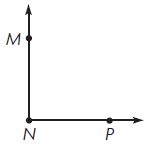
m∠MNP = ____ °

Answer: m∠MNP = 90°

By observing the above figure we can say that the angle of m∠MNP is 90°

Question 3.

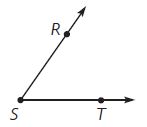
m∠RST = ____ °

Answer: m∠RST = 65°
By using the protractor we can measure m∠RST = 65°

Use a protractor to draw the angle.

Question 4.
40°

Answer:

Question 5.
170°

Answer:

Draw an example of each. Label the angle with its measure.

Question 6.
a right angle

Answer:

A right angle is an angle of exactly 90°

Question 7.
an acute angle

Answer:

The acute angle is the small angle which is less than 90°.

Problem Solving

The drawing shows the angles a stair tread makes with a support board along a wall. Use your protractor to measure the angles.

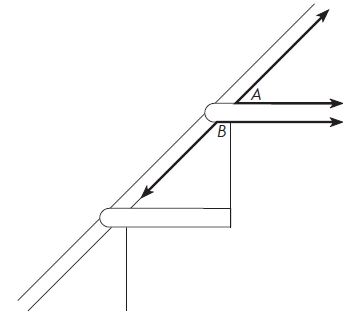
Question 8.
What is the measure of ∠A?
____ °

Answer: 45°

By using the protractor we can measure the angle for A = 45°

Question 9.
What is the measure of ∠B?
____ °

Answer: 135°

The same process is used to measure ∠B = 135°

Common Core – New – Page No. 618

Lesson Check

Question 1.
What is the measure of ∠ABC?

Options:
a. 15°
b. 25°
c. 155°
d. 165°

Answer: 15°

Explanation:

Step 1: Place the center point of the protractor on the point B.
Step 2: Align the 0° mark on the scale of the protractor with ray BC.
Step 3: Find the point where AC meet. Read the angle measure on that scale.
So, the measure of ∠ABC is 15°
Thus the correct answer is option A.

Question 2.
What is the measure of ∠XYZ?

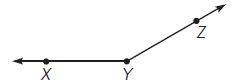
Options:
a. 20°
b. 30°
c. 150°
d. 160°

Answer: 150°

Explanation:

Step 1: Place the center point of the protractor on the point Y.
Step 2: Align the 0° mark on the scale of the protractor with ray XY.
Step 3: Find the point where YZ meet. Read the angle measure on that scale.
So, ∠XYZ = 150°
Therefore the correct answer is option C.

Spiral Review

Question 3.
Derrick earned $1,472 during the 4 weeks he had his summer job. If he earned the same amount each week, how much did he earn each week?
Options:
a. $360
b. $368
c. $3,680
d. $5,888

Answer: $368

Explanation:

Given that, Derrick earned $1,472 during the 4 weeks he had his summer job.
Let the amount he earned per week = x
x × 4 = $1,472
x = 1472 ÷ 4
x = 1472/4 = 368
So, Derrick earned $368 per week.

Question 4.
Arthur baked 1 \(\frac{7}{12}\) dozen muffins. Nina baked 1 \(\frac{1}{12}\) dozen muffins. How many dozen muffins did they bake in all?
Options:
a. 3 \(\frac{2}{3}\)
b. 2 \(\frac{2}{3}\)
c. 2 \(\frac{1}{2}\)
d. \(\frac{6}{12}\)

Answer: 2 \(\frac{2}{3}\)

Explanation:

Given:
Arthur baked 1 \(\frac{7}{12}\) dozen muffins. Nina baked 1 \(\frac{1}{12}\) dozen muffins.
Add both the fractions
Convert mixed fraction into normal fractions
1 \(\frac{7}{12}\) = \(\frac{19}{12}\)
1 \(\frac{1}{12}\) = \(\frac{13}{12}\)
\(\frac{19}{12}\) + \(\frac{13}{12}\) = \(\frac{32}{12}\)
= \(\frac{8}{3}\)
Convert \(\frac{8}{3}\) into mixed fraction = 2 \(\frac{2}{3}\)
So, the answer is option B.

Question 5.
Trisha drew the figure below. What figure did she draw?

Options:
a. line segment ST
b. ray ST
c. ray TS
d. line TS

Answer: ray TS

A ray can be defined as a part of a line that has a fixed starting point but no endpoint.
Here the point starts from T and ends at S.
So, the figure Trisha drew is ray TS.
The correct answer is option C.

Question 6.
Which describes the turn shown by the angle?

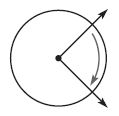
Options:
a. 1 full turn clockwise
b. \(\frac{3}{4 }\) turn clockwise
c. \(\frac{1}{2}\) turn clockwise
d. \(\frac{1}{4}\) turn clockwise

Answer: \(\frac{1}{4}\) turn clockwise

Explanation:

The figure shows that the point turned \(\frac{1}{4}\) in clockwise direction.
So, the answer is option D.

Page No. 619

Choose the best term from the box.

Question 1.
The unit used to measure an angle is called a ________.
________

Answer: The unit used to measure an angle is called a degree.

Question 2.
________ is the opposite of the direction in which the hands of a clock move.
________

Answer: Counterclockwise is the opposite of the direction in which the hands of a clock move.

Question 3.
A ________ is a tool for measuring the size of an angle.
________

Answer: A protractor is a tool for measuring the size of an angle.

Tell whether the angle on the circle shows a \(\frac{1}{4}, \frac{1}{2}, \frac{3}{4}\), or 1 full turn clockwise or counterclockwise.

Question 4.

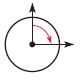
\(\frac{□}{□}\)

Answer: \(\frac{1}{4}\) turn clockwise
The figure shows that the angle turn \(\frac{1}{4}\) in the clockwise direction.

Question 5.

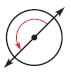
\(\frac{□}{□}\)

Answer: \(\frac{1}{2}\) turn counterclockwise
From the above figure, we can see that the angle turn \(\frac{1}{2}\) in the counterclockwise direction.

Question 6.

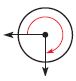
\(\frac{□}{□}\)

Answer: \(\frac{3}{4}\) turn clockwise
The figure shows that the angle turn \(\frac{3}{4}\) in the clockwise direction.

Question 7.

____

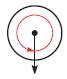
Answer: \(\frac{1}{1}\) or 1 turn counterclockwise
From the above figure, we can see that the angle turn \(\frac{1}{1}\) or 1 in the counterclockwise direction.

Tell the measure of the angle in degrees.

Question 8.

____ °

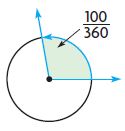
Answer: 100°

\(\frac{100}{360}\) × 360° = 100°

Question 9.
____ °

Use a protractor to draw the angle.

Question 10.
75°
Type below:
________

Question 11.
127°
Type below:
________

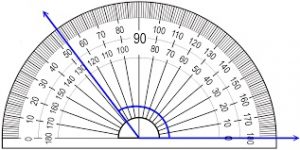
Page No. 620

Question 12.
Phillip watched a beach volleyball game from 1:45 p.m. to 2:00 p.m. How many degrees did the minute hand turn?

____ °

Answer: 90°

Explanation:

Phillip watched a beach volleyball game from 1:45 p.m. to 2:00 p.m.
The minute hand turned for 15 minutes.
That means \(\frac{1}{4}\) turn clockwise.
Complete angle = 360°
\(\frac{1}{4}\) × 360° = 360°/4 = 90°
Therefore the minute hand turn 90°

Question 13.
What angle does this piece of pie form?

____ °

Answer: 180°

From the above figure, we can see that half of the pie is completed.
Complete angle = 360°
\(\frac{1}{2}\) × 360°
= 180°
The angle for the piece of pie form is 180°

Question 14.
What is m∠CBT? Use a protractor to help you.

____ °

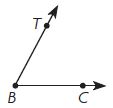
Answer: 60°

By using the protractor we can say that the angle for the above figure is 60°

Question 15.
Matt cut a circle into 8 equal sections. He drew an angle that measures the same as the total measure of 3 of the sections in the circle. What is the measure of the angle Matt drew?
____ °

Answer: 135°

Explanation:

Matt cut a circle into 8 equal sections.
He drew an angle that measures the same as the total measure of 3 of the sections in the circle.
Complete angle = 360°
Divide the total number of sections by 360°
\(\frac{360}{8}\) = 45°
So, the angle for each section is 45°
The angle for 3 of the sections in the circle = 3 × 45° = 135°
Thus the measure of the angle Matt drew is 135°

Page No. 623

Add to find the measure of the angle. Write an equation to record your work.

Question 1.

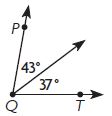
∠PQT = ____ °

Answer: 80°

To find the ∠PQT you have to add 43° and 37°
∠PQT = 43° + 37°
∠PQT = 80°

Question 2.

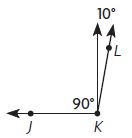
∠JKL = ____ °

Answer: 100°
Let ∠JKL = x°
∠JKL = 90° + 10°
∠JKL = 100°

Question 3.

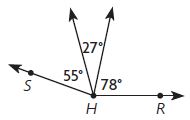
∠RHT = ____ °

Answer:
Let ∠RHT = x°
x = 55° + 27° + 78°
x = 160°
Therefore ∠RHT = 160°

Use a protractor to find the measure of each angle. Label each angle with its measure.
Write the sum of the angle measures as an equation.

Question 4.

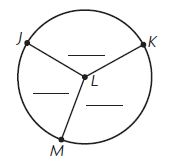
Type below:
________

Answer:

By using the protractor we can measure the angles of the above figures.
m∠KLM = 160°
m∠KLJ = 80°
m∠LMJ = 120°

Question 5.

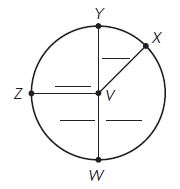
Type below:
________

Answer:

By using the protractor we can measure the angles of the above figures.

m∠WVZ = 90°
m∠YVZ = 90°
m∠WVX = 140°
m∠YVX = 40°

Question 6.
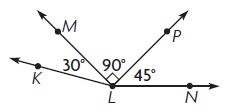
Use Diagrams What is m∠QRT?

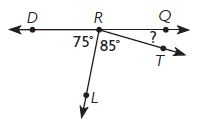
∠QRT = ____ °

Answer: 20°

The above figure is a straight angle.
∠QRT + ∠LRD + ∠RLT = 180
∠QRT + 75° + 85° = 180°
∠QRT + 160° = 180°
∠QRT = 180°- 160°
∠QRT = 20°

Question 7.
Look back at Exercise 1. Suppose you joined an angle measuring 10° to ∠PQT. Draw the new angle, showing all three parts. What type of angle is formed?
Type below:
________

Page No. 624

Question 8.
Stephanie, Kay, and Shane each ate an equal-sized piece of a pizza. The measure of the angle of each piece was 45°. When the pieces were together, what is the measure of the angle they formed?

a. What are you asked to find?
Type below:
________

Answer: What is the measure of the angle for the pizza leftover?

Question 8.
b. What information do you need to use?
Type below:
________

Answer: I need the information about the angle for each piece of pizza.

Question 8.
c. Tell how you can use addition to solve the problem.
Type below:
________

Answer:
The measure of the angle of each piece was 45°
There are 3 pieces of pizza = 45° + 45° + 45° = 135°

Question 8.
d. Complete the sentence. The three pieces of pizza formed a _________ angle.
________

Answer: Obtuse angle

Question 9.
What is the measure of ∠XZW?

____ °

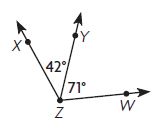
Answer: 113°

Explanation:

∠XZW = ∠XZY + ∠YZW
∠XZY = 42°
∠YZW = 71°
∠XZW = 42° + 71°
∠XZW = 113°

Question 10.
What is m∠PRS? Use equations to explain and check your answer.

____ °

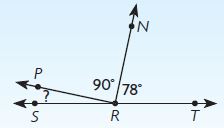
Answer: 12°

Explanation:

The above figure is a straight angle.
The sum of the three angles must be equal to 180°
m∠PRS + m∠PRN + m∠TRN = 180°
m∠PRS + 90° + 78° = 180°
m∠PRS = 180° – 90° – 78°
m∠PRS = 12°

Common Core – New – Page No. 625

Join and Separate Angles

Add to find the measure of the angle. Write an equation to record your work.

Question 1.

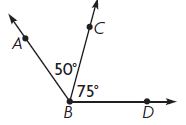
50°+75° = 125°
m∠ABD = 125°

Explanation:

m∠ABC = 50°
m∠CBD = 75°
To find the measure of m∠ABD we have to add m∠ABC and m∠CBD
m∠ABD = 50°+75°
m∠ABD = 125°

Question 2.

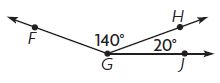
____ ° + ____ ° = ____ ° ;   m∠FGJ = ____ °

Answer: 140° + 20° = 160°
m∠FGJ = 160°

Explanation:

m∠FGH = 140°
m∠JGH = 20°
To find the measure of m∠FGJ we need to add m∠FGH and m∠JGH
m∠FGJ = 140° + 20°
m∠FGJ = 160°

Question 3.

____ ° + ____ ° = ____ ° ; m∠KLN = ____ °

Answer: 30° + 90° + 45° = 165°
m∠KLN = 165°

Explanation:

m∠KLM = 30°
m∠MLP = 90°
m∠PLN = 45°
To find the measure of m∠KLN we need to add m∠KLM, m∠MLP and m∠PLN
m∠KLN = 30° + 90° + 45° = 165°
m∠KLN = 165°

Use a protractor to find the measure of each angle in the circle.

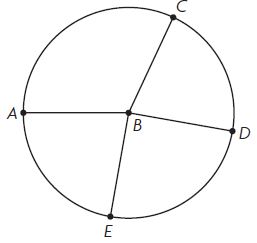
Question 4.
m∠ABC = ____ °

Answer: 115°

Question 5.
m∠DBE = ____ °

Answer: 90°

Question 6.
m∠CBD = ____ °

Answer: 75°

Question 7.
m∠EBA = ____ °

Answer: 80°

Question 8.
Write the sum of the angle measures as an equation.
____ ° + ____ ° + ____ ° + ____ ° = ____ °

Answer:

Sum all the angles = m∠DBE + m∠ABC + m∠CBD + m∠EBA
= 115° + 90° + 75° + 80° = 360°

Problem Solving

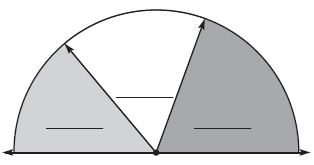
Question 9.
Ned made the design at the right. Use a protractor. Find and write the measure of each of the 3 angles.
____ ° ; ____ ° ; ____ ° ;

Answer: 50°; 60°; 70°

The above figure is a straight angle.
By using the protractor we can measure the angles of the above figure.
The angle of above 3 shades is 50°; 60°; 70°

Question 10.
Write an equation to find the measure of the total angle.
____ ° + ____ ° + ____ ° = ____ °

Answer: Sum of three angles = 50° + 60° + 70° = 180°

Common Core – New – Page No. 626

Lesson Check

Question 1.
What is the measure of m∠WXZ?

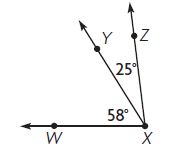
Options:
a. 32°
b. 83°
c. 88°
d. 97°

Answer: 83°

Explanation:

m∠WXZ = m∠WXY + m∠YXZ
Let m∠WXZ be x°
x° = 58° + 25°
x° = 83°
Thus the correct answer is option B.

Question 2.
Which equation can you use to find the m∠MNQ?

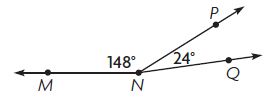
Options:
a. 148° – 24° = ■
b. 148° × 24° = ■
c. 148° ÷ 24° = ■
d. 148° + 24° = ■

Answer: 148° + 24° = ■

Explanation:

To measure the unknown angle we need to add both the angles
m∠MNQ = m∠MNP + m∠PNQ
■ = 148° + 24°
So, the correct answer is option D.

Spiral Review

Question 3.
Joe bought 6 packages of envelopes. Each package contains 125 envelopes. How many envelopes did he buy?
Options:
a. 750
b. 723
c. 720
d. 650

Answer: 750

Explanation:

Joe bought 6 packages of envelopes.
Each package contains 125 envelopes.
To find the total number of envelopes in all 6 packages
We have to multiply number of packages and number of envelopes
= 125 × 6 =750
Thus Joe bought 750 envelopes.
The correct answer is option A.

Question 4.
The Lake Trail is \(\frac{3}{10}\) mile long and the Rock Trail is \(\frac{5}{10}\) long. Bill hiked each trail once. How many miles did he hike in all?
Options:
a. \(\frac{1}{5}\) mile
b. \(\frac{4}{10}\) mile
c. \(\frac{1}{2}\) mile
d. \(\frac{8}{10}\) mile

Answer: \(\frac{8}{10}\) mile

Explanation:

The Lake Trail is \(\frac{3}{10}\) mile long and the Rock Trail is \(\frac{5}{10}\) long. Bill hiked each trail once.
We need to both the fractions
\(\frac{3}{10}\) +\(\frac{5}{10}\)
The denominators are common. So add the numerators.
= \(\frac{8}{10}\)
Bill hiked \(\frac{8}{10}\) miles in all.
Thus the correct answer is option D.

Question 5.
Ron drew a quadrilateral with 4 right angles and 4 sides with the same length. Which best describes the figure he drew?
Options:
a. square
b. rhombus
c. trapezoid
d. parallelogram

Answer: square

Explanation:

A square has got 4 sides of equal length and 4 right angles (right angle = 90 degrees).
So, the answer is option A.

Question 6.
How many degrees are in an angle that turns through \(\frac{3}{4}\) of a circle?
Options:
a. 45°
b. 90°
c. 180°
d. 270°

Answer: 270°

Explanation:

Complete angle = 360°
To measure the angle that turns through is \(\frac{3}{4}\)
multiply \(\frac{3}{4}\) with 360°
360° × \(\frac{3}{4}\) = 270°
So, the answer is option D.

Page No. 629

Question 1.
Laura cuts a square out of scrap paper as shown. What is the angle measure of the piece left over?
First, draw a bar model to represent the problem.

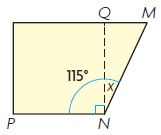
Type below:
_________

Question 1.
Next, write the equation you need to solve.
Type below:
_________

Answer:

m∠MNQ + m∠QNP = m∠MNP
x + 90° = 115°
x = 115° – 90°

Question 1.
Last, find the angle measure of the piece left over.
m∠MNQ =
So, the angle measure of the piece left over is _____.
____ °

Answer:
x + 90° = 115°
x = 115° – 90°
x = 25°
So, the angle measure of the piece left over is 25°

Question 2.
Jackie trimmed a piece of scrap metal to make a straight edge as shown. What is the measure of the piece she trimmed off?

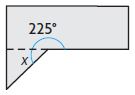
x = ____ °

Answer:
x + 180° = 225°
x = 225°- 180°
x = 45°
Thus the measure of the piece she trimmed off is 45°

Question 3.
What if Laura cut a smaller square as shown? Would m∠MNQ be different? Explain.

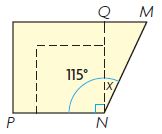
Type below:
_________

Answer: No
m∠MNQ would still be 25°. Only the size of the square changed the angle will be the same.
m∠PNQ and m∠MNP did not change.

Question 4.
The map shows Marco’s paper route. When Marco turns right onto Center Street from Main Street, what degree turn does he make? Hint: Draw a dashed line to extend Oak Street to form a 180° angle.

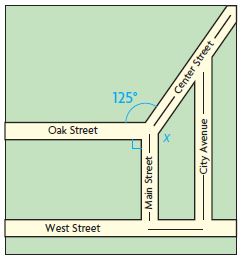
Answer:

x° + 125° + 180° = 360°
x° = 360° – 125° – 180°
x° = 360° – 215°
x° = 145°

Page No. 630

Question 5.
Write an Equation Two angles form a straight angle. One angle measures 89°. What is the measure of the other angle? Explain.
____ °

Answer: 91°

A straight angle measures 180°, so you can subtract 89° from 180°
180° – 89° = 91°

Question 6.
Pose a Problem Look back at Problem 5. Write a similar problem about two angles that form a right angle.
____ °

Answer: Two angles form a right angle. The measure of one angle is 25°. What is the measure of the other angle?
x + 25° = 90°
x °= 90° – 25°
x° = 65°
The measure of other angle is 65°

Question 7.
Sam paid $20 for two T-shirts. The price of each T-shirt was a multiple of 5. What are the possible prices of the T-shirts?
Type below:
_________

Answer:
Sam paid $20 for two T-shirts.
The price of each T-shirt was a multiple of 5.
$20 – 2 T-shirts
x – 1 T-shirt
x = $10
The possible prices of the T-shirts are $10, $10
Another possible price of the T-shirts are $5, $15

Question 8.
Zayna has 3 boxes with 15 art books in each box. She has 2 bags with 11 math books in each bag. If she gives 30 books away, how many art and math books does she have left?
_____ books

Answer: 37 art and math books

Explanation:

Zayna has 3 boxes with 15 art books in each box = 15 × 3 = 45
She has 2 bags with 11 math books in each bag = 11 × 2 = 22
Total number of books = 45 + 22 = 67
If she gives 30 books away, then we have to subtract 30 from 67
67 – 30 = 37
37 art and math books are left.

Question 9.
What’s the Question? It measures greater than 0° and less than 90°.
Type below:
_________

Answer: What is an acute angle?

Question 10.
Two angles, ∠A and ∠B, form a straight angle. ∠A measures 65°. For numbers 10a–10c, select True or False for the statement.
a. ∠B is an acute angle.
i. True
ii. False

Answer: False

Explanation:

Two angles, ∠A and ∠B, form a straight angle. ∠A measures 65°.
65° + ∠B = 180°
∠B = 180° – 65°
∠B = 115°
115° is not an acute angle.
So, the above statement is false.

Question 10.
b. The equation 180° – 65° = x° can be used to find the measure of ∠B.
i. True
ii. False

Answer: True

Question 10.
c. The measure of ∠B is 125°.
i. True
ii. False

Answer: False

65° + ∠B = 180°
∠B = 180° – 65°
∠B = 115°
So, the above statement is false.

Common Core – New – Page No. 631

Problem Solving Unknown Angle Measures

Solve each problem. Draw a diagram to help.

Question 1.

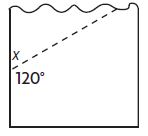
Question 2.
An artist is cutting a piece of metal as shown. What is the angle measure of the piece left over?

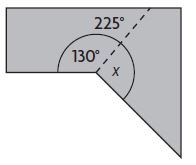
x = ____ °

Answer: 95°

x + 130° = 225°
x = 225° – 130°
x = 95°
Therefore the angle of the piece leftover is 95°.

Question 3.
Joan has a piece of material for making a costume. She needs to cut it as shown. What is the angle measure of the piece left over?

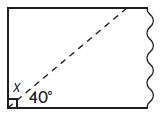
x = ____ °

Answer: 50°

Joan has a piece of material for making a costume. She needs to cut it as shown.
By seeing the above figure we can say that it is a right angle.|
The sum of two must be equal to 90°
Let the unknown angle be x
x + 40° = 90°
x = 90° – 40°
x = 50°
Thue the angle measure of the piece leftover is 50°

Common Core – New – Page No. 632

Lesson Check

Question 1.
Angelo cuts a triangle from a sheet of paper as shown. What is the measure of ∠x in the triangle?

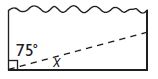
Options:
a. 15°
b. 25°
c. 75°
d. 105°

Answer: 15°

Explanation:

The above figure is a right angle.
So, to measure the ∠x we have to subtract 75° from 90°
∠x + 75° = 90°
∠x = 90° – 75°
∠x = 15°
Thus the correct answer is option A.

Question 2.
Cindy cuts a piece of wood as shown. What is the angle measure of the piece left over?

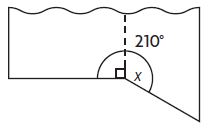
Options:
a. 30°
b. 90°
c. 120°
d. 150°

Answer: 120°

Explanation:

x + 90° = 210°
x = 210° – 90°
x = 120°
120° is the measure of the piece leftover.
So, the correct answer is option C.

Spiral Review

Question 3.
Tyronne worked 21 days last month. He earned $79 each day. How much did Tyronne earn last month?
Options:
a. $869
b. $948
c. $1,659
d. $2,169

Answer: $1,659

Explanation:

Tyronne worked 21 days last month.
He earned $79 each day.
$79 × 21 = 1659
Thus Tyronne earned $1,659 last month.
So, the correct answer is option C.

Question 4.
Meg inline skated for \(\frac{7}{10}\) mile. Which shows this distance written as a decimal?
Options:
a. 0.07 mile
b. 0.1 mile
c. 0.7 mile
d. 7.1 miles

Answer: 0.7 mile

Explanation:

Meg inline skated for \(\frac{7}{10}\) mile.
The decimal of the fraction \(\frac{7}{10}\) is 0.7
So, the answer is option C.

Question 5.
Kerry ran 34 mile. Sherrie ran \(\frac{1}{2}\) mile. Marcie ran \(\frac{2}{3}\) mile. Which list orders the friends from least to greatest distance
run?
Options:
a. Kerry, Sherrie, Marcie
b. Kerry, Marcie, Sherrie
c. Sherrie, Kerry, Marcie
d. Sherrie, Marcie, Kerry

Answer: Sherrie, Marcie, Kerry

Explanation:

Kerry ran 34 miles. Sherrie ran \(\frac{1}{2}\) mile. Marcie ran \(\frac{2}{3}\) mile.
The order of the above fractions is Sherrie ran \(\frac{1}{2}\), \(\frac{2}{3}\), 34
The distance from least to greatest is Sherrie, Marcie, Kerry.
so, the correct answer is option D.

Question 6.
What is the measure of m∠ABC?

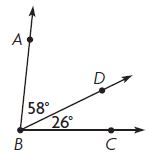
Options:
a. 32°
b. 84°
c. 88°
d. 94°

Answer: 84°

Explanation:

m∠ABC = m∠ABD + m∠DBC
m∠ABC = 58° + 26°
m∠ABC = 84°
So, the correct answer is option B.

Page No. 633

Question 1.
An angle represents \(\frac{1}{12}\) of a circle. Use the numbers to show how to find the measure of the angle in degrees.



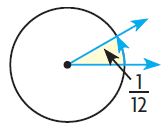
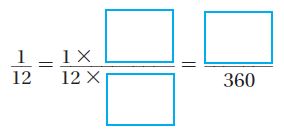
The angle measure is ____ °

Answer: 30°
\(\frac{1}{12}\) × \(\frac{30}{30}\) = \(\frac{30}{360}\)
Thus the angle measure is 30°

Question 2.
Match the measure of each ∠C with the measure of ∠D that forms a straight angle.

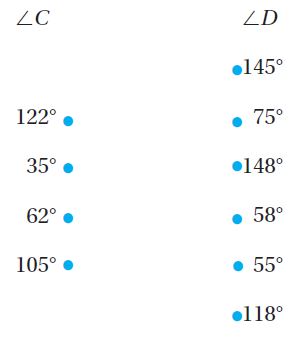
Type below:
_________

i. 122° + 58° = 180°
ii. 35° + 145° = 180°
iii. 62° + 118° = 180°
iv. 105° + 75° = 180°

Question 3.
Katie drew an obtuse angle. Which could be the measure of the angle she drew? Mark all that apply.
Options:
a. 35°
b. 157°
c. 180°
d. 92°

Answer: 157° and 92°
An obtuse angle has a measurement greater than 90 degrees but less than 180 degrees.
From the above options, B and D are more than 90°
So, the answer is option B and D.

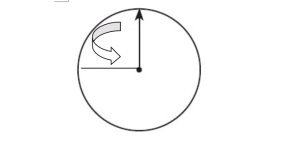
Question 4.
Draw an angle that represents a \(\frac{1}{4}\) turn counterclockwise on the circle.

Type below:
_________

Page No. 634

Question 5.
Renee drew the figure shown. For 5a–5c, select Yes or No to tell whether the statement is true.

a. The measure of a straight angle is 180°.
i. yes
ii. no

Answer: Yes

By seeing the above figure we can say that the angle is a straight angle.
So, the above statement is true.

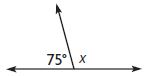
Question 5.
b. To find the measure of x, Renee can subtract 75° from 180°.
i. yes
ii. no

Answer: Yes

To know the value of x we have to subtract 75° from 180°.
x = 180° – 75°
Thus the above statement is true.

Question 5.
c. The measure of x is 115°.
i. yes
ii. no

Answer: No
x = 180° – 75°
x = 105°
Thus the above statement is false.
So, the answer is no.

Question 6.
Trey drew this figure with a protractor.

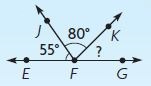
Part A
Write an equation that can be used to find m∠KFG.
Type below:
_________

Answer: 55° + 80° + x = 180°

The figure is a straight angle.
So, the sum of the three angles must be equal to 180°
Let m∠KFG = x
55° + 80° + x = 180°

Question 6.
Part B
What is the measure of m∠KFG? Describe how you solved the equation and how you can check your answer.
____ °
Explain:
_________

Answer: 45°

Explanation:

55° + 80° + x = 180°
x = 180° – 80° – 55°
x = 45°

Question 7.
Use a protractor to find the measure of the angle.

The angle measures ____ °

Answer: 40°
By using a protractor we can measure the angle.
The angle of the above figure is 40°

Page No. 635

Question 8.
Alex drew this angle on the circle. Which describes the angle? Mark all that apply.

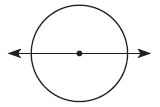
Options:
a. \(\frac{1}{4}\) turn
b. clockwise
c. \(\frac{1}{2}\) turn
d. counterclockwise

Answer: \(\frac{1}{2}\) turn

The above figure shows that it is straight angle. So, the fraction of the circle is \(\frac{1}{2}\) turn.
The correct answer is option C.

Question 9.
Miles has a piece of paper that is \(\frac{1}{4}\) of a large circle. He cuts the paper into three equal parts from the center point of the circle. What is the angle measure of each part?

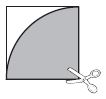
The angle measure is ____ °

Answer: 30°

Explanation:

Miles has a piece of paper that is \(\frac{1}{4}\) of a large circle. He cuts the paper into three equal parts from the center point of the circle.
\(\frac{1}{4}\) of a large circle = 90°
Given that he cut into 3 equal parts = \(\frac{90}{3}\) = 30°
So, the angle for each part is 30°

Question 10.
Use a protractor to find the measure of each angle. Write each angle and its measure in a box ordered by the measure of the angles from least to greatest.

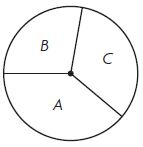
Answer:

Question 11.
Use the numbers and symbols to write an equation that can be used to find the measure of the unknown angle.

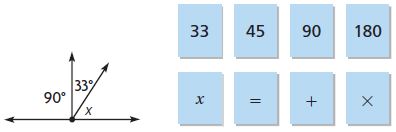
What is the measure of the unknown angle?
____ °

Answer: 57°

Explanation:

Let the unknown angle be x
It is a straight angle.
The sum of three angles = 180°
90° + 33° + x = 180°
x = 180° – 90° – 33°
x = 57°

Page No. 636

Question 12.
Choose the word or number to complete a true statement about m∠JKL.


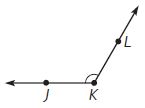
m∠JKL is a(n) ______ angle that has a measure of ____ °.

Answer: m∠JKL is an Obtuse angle that has a measure of 120°.

Question 13.
Vince began practicing piano at 5:15 p.m. He stopped at 5:35 p.m. How many degrees did the minute hand turn during Vince’s practice time?
Explain how you found your answer.

____ °
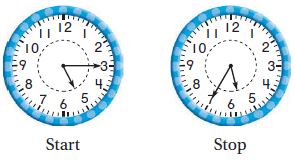
Explain:
_________

Answer: 120°

I shaded the part of the clock that the minute hand turned from 5:15 p.m. to 5:35 p.m. anmd found that it is \(\frac{1}{3}\) of the circle.
Next, I multiplied \(\frac{1}{3}\) × 360° = 120°
Thus the minute hand moved 120°

Question 14.
An angle measures 125°. Through what fraction of a circle does the angle turn?
\(\frac{□}{□}\) of a circle

Answer: \(\frac{125}{360}\)

The fraction of the circle the angle turned is \(\frac{125}{360}\)

Question 15.
Write the letter for each angle measure in the correct box.

Type below:
__________

Answer:

Page No. 637

Question 16.
For numbers 16a–16b, select the fraction that makes a true statement about the figure.

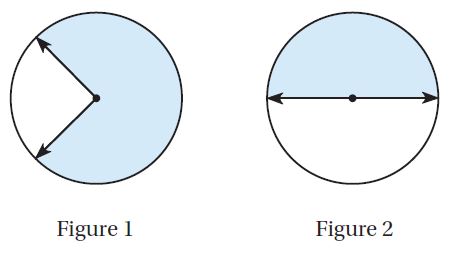
Question 16.
a. The angle in Figure 1 represents a turn.
\(\frac{□}{□}\) turn

Answer: The angle in Figure 1 represents a \(\frac{3}{4}\) turn

The above figure shows that \(\frac{3}{4}\) part of the circle is shaded. So, the angle represents \(\frac{3}{4}\) turn.

Question 16.
b. The angle in Figure 2 represents a 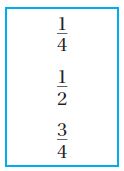turn.
\(\frac{□}{□}\) turn

Answer: The angle in Figure 2 represents a \(\frac{1}{2}\) turn.
From the second figure, we observe that half of the circle is shaded. So, The angle in Figure 2 represents a \(\frac{1}{2}\) turn.

Question 17.
Melanie cuts a rectangle out of a piece of scrap paper as shown. She wants to calculate the angle measure of the piece that is left over.

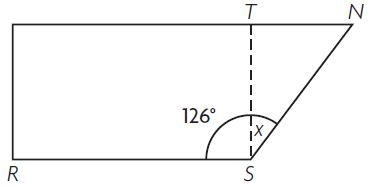
Part A
Draw a bar model to represent the problem.

Question 17.
Part B
Write and solve an equation to find x.
The angle measures ____ °.

Answer: 36°
m∠RST = 90°
m∠RSN = 126°
m∠TSN = x°
x + 90° = 126°
x = 126° – 90°
x = 36°
m∠TSN = 36°

Page No. 638

Question 18.
Two angles, m∠A and m∠B, form a right angle. m∠A measures 32°.
For numbers, 18a–18c, select True or False for the statement.
a. m∠B is an acute angle.
i. True
ii. False

Answer: True

If the sum of two angles is 90°, if one angle is acute then the other angle will be acute.
So, the above statement is true.

Question 18.
b. The equation 180° − 32° = x° can be used to find the measure of m∠B.
i. True
ii. False

Answer: False

Explanation:

Given that the sum of 2 angles is 90°
The sum of m∠A and m∠B = 90°
90° – 32° = x°
So, the above statement is false.

Question 18.
c. The measure of m∠B is 58°.
i. True
ii. False

Answer: True

Explanation:

Let m∠B = x
x° + 32° = 90°
x = 90 – 32
x = 58°.
So, the above statement is true.

Question 19.
A circle is divided into parts. Which sum could represent the angle measures that make up the circle? Mark all that apply.
Options:
a. 120° + 120° + 120° + 120°
b. 25° + 40° + 80° + 105° + 110°
c. 33° + 82° + 111° + 50° + 84°
d. 40° + 53° + 72° + 81° + 90° + 34°

Answer: 25° + 40° + 80° + 105° + 110°; 33° + 82° + 111° + 50° + 84°

Explanation:

The sum of all the angles must be equal to 360°
i. 120° + 120° + 120° + 120° = 480° ≠ 360°
ii. 25° + 40° + 80° + 105° + 110° = 360°
iii. 33° + 82° + 111° + 50° + 84° = 360°
iv. 40° + 53° + 72° + 81° + 90° + 34° = 370° ≠ 360°
So, the correct answers are option B, C.

Question 20.
Use a protractor to find the measures of the unknown angles.

What do you notice about the measures of the unknown angles? Is this what you would have expected? Explain your reasoning.
m∠x = ____ ° m∠y = ____ °

Answer: m∠x = 70°; m∠y = 110°
By using a protractor we can find the measure of m∠y
m∠y = 110°
Let m∠x = x°
Sum of supplementary angles = 180°
110° + x = 180°
x = 180° – 110°
x = 70°
Therefore m∠x = 70°

Page No. 643

Use benchmarks to choose the metric unit you would use to measure each.

Question 1.
mass of a strawberry
__________

Answer: gram
The metric unit used to measure the mass of a strawberry is the gram.

Question 2.
length of a cell phone
__________

Answer: Centimeter
The metric unit used to measure the length of a cell phone is Centimeter.

Circle the better estimate.

Question 3.
width of a teacher’s desk
10 meters or 1 meter
__________

Answer: 1 meter
The estimation of the width of the teacher’s desk is 1 meter.

Question 4.
the amount of liquid a punch bowl holds
2 liters or 20 liters
__________

Answer: 2 liters

20 liters is greater than 2 liters.
The estimation of the amount of liquid a punch bowl holds is 2 liters.

Question 5.
distance between Seattle and San Francisco
6 miles or 680 miles
__________

Answer: 680 miles
The distance between Seattle and San Francisco is 680 miles.

Use benchmarks to choose the customary unit you would use to measure each.

Question 6.
length of a football field
__________

Answer: Yard
The units to measure the length of a football field is Yards.

Question 7.
weight of a pumpkin
__________

Answer: Pound
The customary unit I use to measure the weight of a pumpkin is pounds.

Circle the better estimate.

Question 8.
weight of a watermelon
4 pounds or 4 ounces
__________

Answer: 4 pounds
The estimation of the weight of watermelon is 4 pounds.

Question 9.
the amount of liquid a fish tank holds
10 cups or 10 gallons
__________

Answer: 10 gallons
The estimation of the amount of liquid a fish tank holds is 10 gallons.

Complete the sentence. Write more or less.

Question 10.
Matthew’s large dog weighs ________ than one ton.
________

Answer: Less
1 ton = 1000 kgs
The weight of dogs can’t be more than a ton.
So, Matthew’s large dog weighs less than one ton.

Question 11.
The amount of liquid a sink can hold is _______ than one cup of water.
________

Answer: More
1 cup holds very less amount of water.
So, The amount of liquid a sink can hold is more than one cup of water.

Question 12.
A paper clip has a mass of _______ than one kilogram.
________

Answer: Less

The weight of a paper clip is about 1 gram.
So, A paper clip has a mass of less than one kilogram.

Page No. 644

For 13–15, use benchmarks to explain your answer.

Question 13.
Cristina is making macaroni and cheese for her family. Would Cristina use 1 pound of macaroni or 1 ounce of macaroni?
__________

Answer: Cristina should use 1 pound of macaroni.

Question 14.
Which is the better estimate for the length of a kitchen table, 200 centimeters or 200 meters?
__________

Answer: 200 centimeters

Centimeters are less than meters. The length of the kitchen will be measured in centimeters.
So, the answer is 200 centimeters.

Question 15.
Jodi wants to weigh her cat and measure its standing height. Which two units should she use?
weight: ________
height: ________

Answer:
The weight of the cat should be measured in Kilograms.
The height of the cat should be measured in Centimeters.

Question 16.
Evaluate Reasonableness Dalton used benchmarks to estimate that there are more cups than quarts in one gallon. Is Dalton’s estimate reasonable? Explain.
Type below:
__________

Answer: Dalton’s reasoning is correct because the measurement of cups is smaller than the measurement of quarts, therefore there would be more cups in a gallon than quarts.

Question 17.
Select the correct word to complete the sentence. Justine is thirsty after running two miles.
She should of water.
__________

Answer: 1 pint

The suitable word for the above sentence is the pint. Pint is a measure for liquid equal to about half a liter. There are eight pints in a gallon.

Conclusion

Make maths as your favorite subject by solving the problems. If you understand the concepts you can prepare the questions on your own. It is an easy and scoring subject compared to all. So, go through the Go Math Grade 4 Solution Key Chapter 11 Angles to secure the highest marks in the exams. If you have doubts regarding the subject you can comment in the below comment box. All the best!!!!